Под информационной технологией понимается процесс, использующий совокупность средств и методов сбора, обработки и передачи данных для получения информации нового качества о состоянии объекта, процесса или явления. Информационные технологии способствуют постоянному динамичному обновлению содержания, организационных форм и методов обучения и воспитания. Использование компьютера для решения профессиональных задач становится обязательным компонентом педагогической деятельности [1].
Применение информационных технологий при изучении «Линейной алгебры» необходимо по следующим причинам. Во-первых, учебный план дисциплины «Математика 1.1» [4] предусматривает на освоение сложной темы «Линейная алгебра» очень мало времени: всего 8 часов лекционных и 12 часов практических занятий. Во-вторых, ни матрицы, ни определители, ни способы и методы исследования и решения систем линейных уравнений не изучаются в школьном курсе математики, т.е. изучаемый материал является новым для большинства первокурсников. В-третьих, «Линейная алгебра» – первая тема математики, с которой студенты начинают осваивать математику вуза, и информационные технологии помогают недавним абитуриентам адаптироваться к новой для них студенческой жизни.
Для качественного использования времени, планируемого на изучение темы «Линейная алгебра», студентам и преподавателям предлагается методическое обеспечение учебного процесса с применением технических средств: одного компьютера, проектора и экрана в одной учебной аудитории.
Цель исследования
Активным внедрением современных образовательных информационных технологий добиться статистически значимого повышения относительных оценок работы студентов по теме «Линейная алгебра» дисциплины «Математика 1.1» по сравнению с относительными оценками централизованного тестирования по школьному курсу математики.
Материалы и методы исследования
Лекционные занятия
Основные определения, формулировки теорем демонстрируются в виде презентации на аудиторном экране; на доске доказываются теоремы, решаются примеры, реализуются другие традиционные моменты лекции.
Например, начать изучение первой темы дисциплины «Математика 1.1» можно, поместив на экран следующую информацию:
Тема 1. Линейная алгебра
Разделы
1.1. Матрицы и действия над ними
1.2. Определители и их вычисление
1.3. Системы линейных уравнений
Определение матрицы. Матрицей размера m*n называется прямоугольная таблица элементов некоторого множества (например, чисел или функций), имеющая m строк и n столбцов.
Элементы, из которых составлена матрица, называются элементами матрицы.
Матрицы могут обозначаться так:

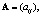
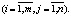
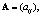
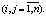
Следует привлечь студентов к обсуждению связи индексов элементов с расположением элементов в матрице, например, при помощи сервиса Mentimeter, подготовив вопросы: «Первый индекс элементов матрицы соответствует…» с альтернативными ответами: «1. Номеру строки», «2. Номеру столбца». Далее с применением слайдов рассматриваются виды матриц, линейные и нелинейные операции над ними с решением на доске примеров, иллюстрирующих рассматриваемые операции.
В разделе «1.2. Определители и их вычисление» для большинства студентов первого курса строгое определение определителя воспринимается как набор огромного количества слов и обозначений, в смысле которых им трудно разобраться. Чтобы с первых лекций не отпугнуть студентов от изучаемого материала, определителем квадратной матрицы можно назвать число, соответствующее этой квадратной матрице. Для числовой матрицы первого порядка таким числом является единственный элемент этой матрицы. После определения понятий миноров и алгебраических дополнений элементов матрицы формулируется без доказательства теорема Лапласа, а в качестве применения этой теоремы получаются правила вычисления определителей второго порядка и третьего порядка методом треугольников и при помощи таблицы Саррюса. С целью заинтриговать студентов рекомендуется познакомить их с общепринятым определением определителя в учебном пособии [7, с. 18]. Все основные свойства определителей рассматриваются с доказательствами. В заключение изучения раздела определяются понятия минора порядка k, базисного минора матрицы, ранга матрицы; предлагаются алгоритмы методов нахождения ранга матрицы, обратной матрицы, а также подчеркиваются общие и различные результаты действий над матрицами и определителями [7, с. 25].
Свойства матриц и определителей
|
Действие |
Матрица Am*n (таблица из m строк и n столбцов) |
Определитель Δ порядка n (число для матрицы An*n) |
|
Транспонирование |
Rang(A) = Rang(AT) |
Δ не изменяется |
|
Перестановка двух строк |
Ранг не изменяется |
Δ меняет знак |
|
Умножение одной строки на число λ ≠ 0 |
Ранг не изменяется |
Δ изменяется в λ раз (Δ умножается на число λ) |
|
Умножение всех строк на число λ |
A изменяется в λ раз (A умножается на число λ) |
Δ изменяется в λn раз (Δ умножается на число λn) |
|
Умножение одной строки на число λ и сложение с соответствующими элементами другой строки |
Ранг не изменяется |
Δ не изменяется |
|
Получение нулевых и пропорциональных строк |
Ранг не изменяется при вычеркивании всех нулевых и пропорциональных строк, кроме одной из ненулевых |
Δ = 0 |
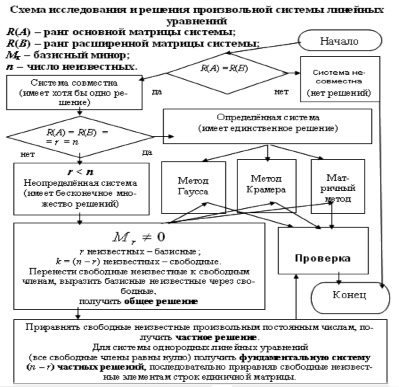
Рис. 1. Схема исследования и решения произвольной системы линейных уравнений
В разделе «1.3. Системы линейных уравнений» весь изложенный материал обобщается схемой исследования и решения произвольной системы линейных уравнений [7, с. 38].
Можно отметить следующие преимущества применения технических средств обучения на лекции. Во-первых, на экране студенты видят правильно написанный текст, в то время как «на слух» информация часто воспринимается с искажениями. Если же писать формулировки определений и теорем на доске, потребуется много дополнительного лекционного времени; во-вторых, каждый студент имеет возможность скопировать на личный электронный носитель все учебные материалы, собранные лектором в одну папку (в том числе и презентации лекционного материала). В-третьих, в потоке занимаются иностранные студенты, для которых визуальное представление информации предпочтительней вербального. Использование лекционных презентаций изменяет характер взаимодействия студентов и преподавателя во время лекции и способствует повышению качества усвоения студентами теоретического материала [11].
Практические занятия
Практическое занятие начинается с объявления темы занятия, обсуждения требуемых для данного практического занятия теоретических положений, рассмотренных на лекциях и в учебных пособиях [6, 7]. На аудиторном экране воспроизводится набор примеров, которые предстоит решать, а также – фрагменты лекционных презентаций, схемы и алгоритмы, если это становится необходимым. Примеры на доске решает студент с помощью преподавателя и других студентов.
Применение такой методики проведения практических занятий позволяет студентам работать в соответствии со своими способностями и знаниями: с более слабыми студентами преподаватель может обсудить возникающие проблемы индивидуально, более сильные студенты выполняют задания самостоятельно и часто – раньше, чем появится решение на доске. У студентов возрастает мотивация к овладению знаниями, уменьшается страх не справиться с решением, студенты приобретают уверенность в своих силах, Работа студента у доски оценивается баллами. Ближняя мотивация повысить рейтинг своих учебных достижений побуждает студентов к активным действиям, поэтому, как правило, часто бывает много желающих работать у доски, так что преподавателю приходится придумывать различные способы отбора одного студента. Например, при помощи подбрасывания игральных костей или обращения к коллективному мнению группы.
На персональном сайте преподавателя [6] размещен набор примеров для практических занятий, с которым студенты могут ознакомиться заранее и подготовиться более основательно к предстоящему практическому занятию.
В конце занятия объявляется тема следующего практического занятия и номера примеров индивидуального домашнего задания.
Самостоятельная работа
В соответствии со своим номером в списке группового журнала студенты получают индивидуальные домашние задания [5, 9].
После 1-го практического занятия выполняются задания на линейные и нелинейные действия над матрицами;
после 2-го практического занятия – на вычисление определителей второго, третьего и более высоких порядков различными методами;
после 3-го – на нахождение обратной матрицы и решение матричных уравнений;
после 4-го и 5-го – на решение линейных неоднородных и однородных систем линейных уравнений методами Крамера и Гаусса.
Проверка индивидуальных работ студентов осуществляется преподавателем с применением пакета MathCAD, т.к. в случае допущенной студентом ошибки ее бывает трудно обнаружить «вручную». Кроме того, заменяя столбцы основной матрицы системы линейных уравнений столбцом свободных членов со свободными неизвестными в числителях формул Крамера, можно получать общее решение неопределенной системы линейных уравнений и методом Крамера [7, с. 40, 8], о чем в учебной литературе упоминаний, как правило, не встречается. Принято утверждать, что в случаях равенства нулю основной матрицы квадратной системы или в случае прямоугольной системы линейных алгебраических уравнений метод Крамера применять нельзя.
На 6-м практическом занятии запланирована контрольная работа. Пропорционально результатам контрольной работы за выполнение примеров индивидуального задания студенту выставляются рейтинговые баллы по формуле с применением пакета Excel. Числитель формулы – количество правильно решенных в ИДЗ примеров – умножается на баллы контрольной работы, а в знаменателе – количество примеров в индивидуальном задании, т.е. в данном случае – 17.
На сайте http://stud.lms.tpu.ru в электронном учебном курсе «Математика 1.1_Тарбокова» студенты самостоятельно выполняют тестовые задания, изучают теоретический материал при помощи инструментов «Книга», «Лекция»; проводят взаимную проверку выполненных индивидуальных заданий с использованием инструмента «Семинар», размещают файлы самостоятельной работы при помощи инструмента «Задание». Все работы, выполненные при помощи инструментов, за исключением инструмента «Книга», оцениваются в баллах в соответствии с запланированными преподавателем для каждого инструмента коэффициентами.
Электронный ресурс является удачным дополнением к традиционным методам обучения. Важным преимуществом использования электронных образовательных ресурсов является то, что студенты сами планируют время работы в электронной среде [10].
Еженедельные консультации по математике позволяют преподавателю помогать студентам в выполнении индивидуальных домашних заданий, а также повышать рейтинговые баллы студентам, решающим дополнительные задания.
Оценку результатов своей работы каждый студент может найти на вкладке персонального сайта преподавателя [6] «Рейтинг учебных достижений студентов», выполненной в пакете Excel.
Результаты исследования и их обсуждение
В Национальном исследовательском Томском политехническом университете для всех студентов-первокурсников в начале первого семестра по школьному курсу математики проводится централизованное тестирование (входной контроль). Относительные оценки входного контроля и контрольной работы по линейной алгебре вычислялись делением полученной студентом оценки на максимально возможную оценку в соответствующем виде контроля.
Сравнение относительных оценок за контрольную работу по линейной алгебре (ОцКР) и относительных оценок входного контроля (ОцВх) позволяет утверждать: студенты, которые не пропускали занятия и выполняли самостоятельно индивидуальные задания, статистически значимо повысили свои относительные оценки.
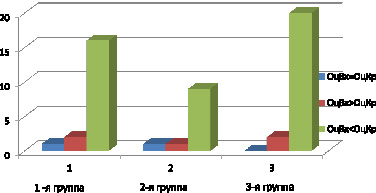
Рис. 2. Сравнение относительных оценок входного тестирования по школьному курсу математики и контрольных работ по линейной алгебре
Заключение
Применение информационных технологий в процессе обучения студентов линейной алгебре позволяет реализовать решение следующих дидактических задач:
- совершенствование организации преподавания, повышение индивидуализации обучения;
- повышение продуктивности самоподготовки студентов;
- индивидуализация работы преподавателя;
- ускорение тиражирования и доступа к достижениям педагогической практики;
- усиление мотивации к обучению;
- активизация процесса обучения, возможность привлечения студентов к исследовательской деятельности;
- обеспечение гибкости процесса обучения [2, 3].
Отрицательные последствия обучения с применением информационных технологий, связанные с дефицитом диалогического общения и отмеченные [3], нивелируются проведением дважды в каждом семестре студенческих конференций, на которых студенты делают сообщения по подготовленным рефератам и презентациям [6].
Библиографическая ссылка
Тарбокова Т.В. ПРИМЕНЕНИЕ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ В ОБУЧЕНИИ СТУДЕНТОВ ЛИНЕЙНОЙ АЛГЕБРЕ // Современные наукоемкие технологии. 2017. № 2. С. 167-171;URL: https://top-technologies.ru/ru/article/view?id=36605 (дата обращения: 03.02.2026).



