В данной статье рассматривается алгоритм определения условного математического ожидания для дискретизированного экспоненциального процесса Леви по времени или состоянию (подробнее см. [3], [8]), которое применяется для вычисления справедливых цен опционов. В моделях со скачками используются следующие способы вычисления цен опционов: методы мультиномиальных деревьев (прост в реализации, но имеет медленную сходимость); метод конечно-разностных схем (быстр, прост). При решении задачи вычисления условного ожидания важно, является ли мера риск-нейтральной. Для экспоненциальных моделей процесса Леви используются методы быстрой факторизации Винера – Хопфа [6] (и для американских опционов) и другие. Целью данной статьи является реализация древовидного алгоритма вычисления условных математических ожиданий для дискретизированного экспоненциального процесса Леви, выбор метода обхода дерева и исследование результатов применения параллельного варианта данного алгоритма на основе многопоточной модели исполнения кода. Задача вычисления условных математических ожиданий имеет достаточно широкий спектр применения, в частности, для определения справедливой цены опционов. Таким образом, данный алгоритм может быть использован для определения условных математических ожиданий случайных процессов данного вида. Кроме того, возможен и прикладной аспект использования указанного алгоритма, например, для вычисления справедливой цены опциона европейского типа, если дисконтированная цена дисконтированного финансового обязательства может быть рассмотрена как дискретизированный экспоненциальный процесс Леви.
Материалы и методы исследования
В основе методики исследования лежит метод деревьев, определение сложности алгоритмов и закон Амдала. Основными в указанном методе являются информационные потоки. Будем считать, что все процессы, которые приводятся в данной статье, изменяются на конечном вероятностном пространстве 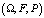 , отсюда число событий на данном вероятностном пространстве будет конечным. Каждая алгебра Fk (k = 0, 1,…, N), где – информация, доступная в момент времени k. При данном рассмотрении каждая фильтрация образует соответствующий слой информационного дерева, причем корню соответствует F0. И таким образом, число слоев у информационного дерева будет равно N + 1. Если интересует некоторое событие, то должны выбрать ту ветку гипотез, которая ему соответствует и рассматривает только эту ветку (подробнее см. [5]). Отсюда, структура данных, которая необходима для реализации алгоритма вычисления условного математического ожидания – это дерево.
, отсюда число событий на данном вероятностном пространстве будет конечным. Каждая алгебра Fk (k = 0, 1,…, N), где – информация, доступная в момент времени k. При данном рассмотрении каждая фильтрация образует соответствующий слой информационного дерева, причем корню соответствует F0. И таким образом, число слоев у информационного дерева будет равно N + 1. Если интересует некоторое событие, то должны выбрать ту ветку гипотез, которая ему соответствует и рассматривает только эту ветку (подробнее см. [5]). Отсюда, структура данных, которая необходима для реализации алгоритма вычисления условного математического ожидания – это дерево.
Результаты исследования и их обсуждение
Общая схема расчетов на дереве представляет собой совокупность двух методов: прохода по дереву от корня к листьями и прохода по дереву от листьев к корню. Напомним, что в корне содержится информация о нулевом моменте времени (входная информация). Итак, при проходе от корня, вычисляется базовый процесс S (можно рассматривать как дисконтированную цену дисконтированного финансового обязательства) и ограниченная функция f (можно считать дисконтированным финансовым обязательством). Если данная функция – опцион европейского типа, то значения f – будут только на листьях, в случае Американского типа значения будут везде кроме корня. При проходе от листьев вычисляются условные математические ожидания, тогда в корне будет находиться значение справедливой цены опциона.
Будем рассматривать дискретизированные экспоненциальные процессы Леви следующего вида:
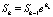 . (1)
. (1)
Итак, индекс hk – случайная величина, которая распределена по закону Пуассона при дискретизации экспоненциального процесса Леви по времени и состоянию (подробнее см. [3], [8]). Для реализации алгоритмов необходимо выяснить, какую структуру имеет информационное дерево, если базовый процесс изменяется по закону (1). Условие на число потомков вершины имеет вид
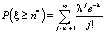 . (2)
. (2)
У вершины получается n* + 1 потомков (подробнее см. [7]).
Дерево реализовано при помощи принципов объектно-ориентированного программирования, узел дерева определен как класс (структура дерева имеет вид как на рис. 1).
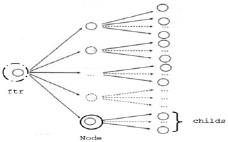
Рис. 1. Реализация дерева
Например, значение S в узле Node – Node > S, если необходимо получить предыдущее значение (нужно для вычисления условных математических ожиданий), то получим, Node > ftr > S.
Следующим этапом является выбор алгоритма обхода дерева. При осуществлении вычислений должно быть построено дерево, и его узлы должны быть обработаны. В данном случае могут использоваться модификации метода «поиска в глубину» и «поиска в ширину». Чаще используется метод поиска в глубину, это связано с тем, что при использовании данного алгоритма дерево не хранится в памяти целиком. Обрабатывается один из путей от корня дерева к листу или какая-то его часть в каждый момент времени.
При решении задачи вычисления условного математического ожидания каждая вершина дерева может быть описана с помощью двух векторов. Обозначим их FRTL (от «from the root to the leaves») и FLTR. Для вычисления этих векторов функции имеют вид
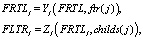 (3)
(3)
где j – номер вершины в дереве, если организовать нумерацию от корня к листам), ftr(j) – вершина, которая является родительской для вершины для j, childs(j) – потомки вершины j.
Заметим, что данная схема является обобщенной (не учитывает особенности вычислений при проходах по дереву). Например, при проходе от корня к листьям вычисляется значение базового процесса S, при проходе от листьев к корню вычисляются условные математические ожидания и в корне определяется справедливая цена.
Поиск в глубину может быть использован в случае, когда операции выделения памяти для размещения всего дерева в памяти требуют достаточно больших временных затрат, либо когда памяти недостаточно для размещения всего дерева.
Заметим, что данные алгоритмы реализованы на языке С++. Операции выделения памяти большинством компиляторов языка C++ достаточно эффективны. Как при выделении непрерывных блоков памяти и не приводят к большим временным затратам, так и в общем. Следовательно, данные издержки не могут привести к многократному замедлению вычислений.
В данном случае алгоритм поиска в глубину может быть применим и является более предпочтительным по времени работы, поскольку не требует хранения дерева полностью в памяти. Но этот факт может быть использован для обоснования в том случае, если объема оперативной памяти достаточно для хранения всего дерева в памяти. При реализации алгоритмов будем использовать «поиск в ширину».
Отметим, что при использовании схем параллельных вычислений будут внесены некоторые особенности в расчеты, а значит, будут изменены базовые алгоритмы обработки деревьев.
Дерево определено в виде класса – class Tree. В данном классе реализованы методы работы с деревом. Соответственно, есть методы, которые реализуют функции (3). Для определения вектора FRTL используется метод forward, для определении вектора FLTR - метод backward, с помощью которого определяются условные математические ожидания.
Рассмотрим реализацию древовидного алгоритма вычисления условных математических ожиданий на примере задачи вычисления условного математического ожидания дискретизированного экспоненциального процесса Леви при решении задачи о среднеквадратичном хедже (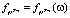 – которое
– которое  – измеримое платежное обязательство – финансовое обязательство европейского типа) (подробнее см. [2]):
– измеримое платежное обязательство – финансовое обязательство европейского типа) (подробнее см. [2]):
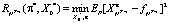 . (4)
. (4)
После решения получим (параметры η, χ – из функции Лагранжа, которая была использована при решении задачи (4)):
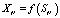 ,
,
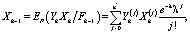
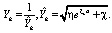
Заметим, что X0 есть справедливая цена опциона.
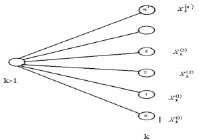
Рис. 2. Пример расчета на дереве
На рис. 2 показан пример расчета, где k – текущий уровень дерева, k – 1 – предыдущий уровень, в данном случае эту вершину уровня k – 1 рассматриваем как родителя вершин уровня k 0, 1, 2,…,n*, а вершины 0, 1, 2,…,n*, как ее потомков.
Одна вершина дерева занимает 48 байт для задачи (4). Оценим число вершин на дереве. Положим, что количество потомков равно семи. Из таблицы видно, что, начиная с 10 уровня, используется достаточно большой объем памяти. Приложение для определения вычисления реализовано на операционной системе MS Windows. Заметим, что структуры данных стандартной библиотеки С++ имеют ограничения на максимальный объем используемой памяти. Кроме того, при нехватке оперативной памяти используют виртуальную память. Обычно виртуальная память реализуется при использовании жесткого диска. Данная память имеет существенно более низкую скорость работы. Отсюда, хранение всего дерева в памяти является нерациональным. Так при временном горизонте, для которого необходимо найти справедливую цену, больше 15, хранить полностью построенное дерево в памяти практически является невозможным. Из таблицы можно также определить объем вычислительных ресурсов.
Расчет используемой памяти
|
Уровни |
Узлы дерева |
Память |
Единица измерения |
|
1 |
1 |
48,00 |
б |
|
2 |
8 |
384,00 |
б |
|
3 |
57 |
2,67 |
Кб |
|
4 |
400 |
18,75 |
Кб |
|
5 |
2801 |
131,30 |
Кб |
|
6 |
19608 |
919,13 |
Кб |
|
7 |
137257 |
6,28 |
Мб |
|
8 |
960800 |
43,98 |
Мб |
|
9 |
6725601 |
307,87 |
Мб |
|
10 |
47079208 |
2,10 |
Гб |
|
11 |
329554457 |
14,73 |
Гб |
|
12 |
2306881200 |
103,13 |
Гб |
|
13 |
16148168401 |
721,88 |
Гб |
|
14 |
113037178808 |
4,93 |
Тб |
|
15 |
791260251657 |
34,54 |
Тб |
|
16 |
5538821761600 |
241,80 |
Тб |
|
17 |
38771752331201 |
1,65 |
Пб |
Другой проблемой, которая возникает при реализации данных алгоритмов, является временная сложность обработки указанных структур данных. Одним из путей решения данной проблемы (не полного) может стать многопоточная модель исполнения кода. Для реализации данного подхода использовался программный интерфейс OpenMP. Реализация параллельных вычислений OpenMP представлена на рис. 3.
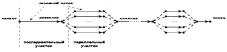
Рис. 3. Реализация параллельных вычислений OpenMP
Заметим, что программа может содержать любое количество последовательных и параллельных участков. Порождение нитей и завершение нитей не влияют сильно (подробнее см. [1]). Древовидные алгоритмы подвергаются глубокому распараллеливанию, поэтому OpenMP может быть использована совместно с другими технологиями параллельного программирования, например с MPI.
Выясним ускорение при использовании многопоточной модели исполнения кода с помощью закона Амдала:
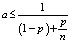 ,
,
где a – ускорение программы, p – доля общего времени выполнения параллельной части программы, n – количество используемых процессоров [4].
Чтобы оценить ускорение, введем следующие допущения: обработка одной вершины, которая измеряется в количестве «обычных» математических операций (основные математические конструкции языка С++ – математические функции и операции), является постоянной величиной, которая не зависит от входных параметров или результатов предыдущих расчетов (в большинстве трудов по оценке алгоритмов обычно пренебрегают). Алгоритм расчета обосновывается на базовом механизме обработки деревьев, «поиск в ширину» и его вид, при котором вершины обрабатываются от листьев к корню дерева. «Поиск в глубину» в случае, когда дерево не может быть размещено полностью в оперативную память, для параллельных расчетов не подходит (было показано выше). Определим сложность последовательных и параллельных алгоритмов. Введем обозначение 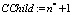 . Число слоев дерева N + 1 (финальный момент времени – N). Тогда число вершин определяется формулой:
. Число слоев дерева N + 1 (финальный момент времени – N). Тогда число вершин определяется формулой:
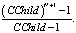
Ускорение для задачи вычисления условного математического ожидания имеет следующую оценку:
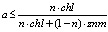 ,
,
где M – глубина управляющего дерева,
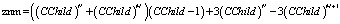 ,
,
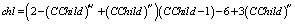 .
.
Ускорение для проверки на ПК со следующими характеристиками - IntelCore(TM)2 DuoCPU, 1,8GHz, RAM 1024Mb, OC Windows Professional (для данного ПК был приведен алгоритм расчета задачи о рандомизированной остановке, подробнее [7]): a ≤ 2. При использовании технологии OpenMP и повторном использовании памяти, глубине управляющего дерева равной четырем и четырьмя потомками, временной горизонт – 10 (финальный момент времени (момент предъявления опциона к исполнению), количество потомков у каждой вершины равно 7, в таблице был показан объем используемой памяти) – время работы составляет 81,255, без использования указанных технологий время работы составило 156,748 сек. Откуда ускорение будет согласно полученным данным меньше или равно двум (1,93).
Заключение
Таким образом, вычислительный алгоритм для определения условных математических ожиданий дискретизированного экспоненциального процесса Леви по времени или состоянию, рассмотренный выше, может быть реализован с помощью древовидного алгоритма. По данным вычислительных экспериментов, при принятии во внимание времени работы и отсутствии ограничений со стороны памяти, выбор метода расчетов на дереве представляется оправданным. Итак, полученный древовидный алгоритм может быть распараллелен с помощью технологии OpenMP и повторного использования памяти (показано на примере ПК со следующими характеристиками - IntelCore(TM)2 DuoCPU, 1,8GHz, RAM 1024Mb, OC Windows Professional), а также и при использовании технологии MPI.
Библиографическая ссылка
Никоненко Н.Д. ДРЕВОВИДНЫЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ УСЛОВНЫХ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ // Современные наукоемкие технологии. 2017. № 2. С. 48-52;URL: https://top-technologies.ru/ru/article/view?id=36583 (дата обращения: 03.02.2026).



