Теория эредитарных процессов получила широкое развитие в последние десятилетия, о чем свидетельствует множество работ как зарубежных [15, 25, 31, 32], так и отечественных авторов [4, 11, 20, 22, 23]. Например, в монографии В.В. Учайкина [11] эредитарным процессам посвящена целая глава. Эредитарные процессы – процессы, обладающие эффектами памяти. Например, в эредитарной системе эффект памяти означает, что текущее состояние системы зависит от ее предыдущих состояний. Поэтому такие процессы описываются с помощью интегро-дифференциальных уравнений, в которых содержатся функции памяти. Если функции памяти имеют степенную зависимость от времени, тогда можно перейти от интегро-дифференциальных уравнений к уравнениям с производными дробных порядков [3]. В этом случае эредитарные процессы иногда называют фрактальными, а порядки дробных производных могут быть связаны с фрактальной размерностью системы, а также зависеть от времени и функции смещения.
Отметим, что дробное исчисление достаточно хорошо изучено и насчитывает более чем 300-ую историю. Отметим такие настольные книги по этой проблематике как [3, 5, 14, 18, 21].
Объектом нашего исследования будут являться эредитарные нелинейные осцилляторы, которые описываются с помощью производных дробных переменных порядков, входящих в модельные уравнения. Такой интерес вызван их многочисленными приложениями [19, 26, 27]. Далее с помощью теории конечно-разностных схем найдем их численные решения. Эта работа является логическим продолжением работы автора [4], где были исследованы математические модели линейных эредитарных колебательных систем.
Отметим также монографию И. Петраса [25], в которой так же были рассмотрены эредитарные колебательные системы, однако в исходных уравнениях были выбраны другие операторы дробных производных, причем их порядки являлись константами.
Постановка и методика решения задач Коши для нелинейных эредитарных осцилляторов
Рассмотрим следующее интегро-дифференциальное уравнение эредитарного осциллятора для функции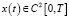 
:
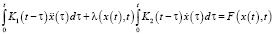, (1)
где 
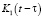и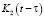 
– ядра, функции памяти, 
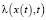– функция, определяющая трения, 
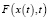– некоторая нелинейная функция, которая определяет тип осциллятора, x(t) – функция смещения, 
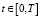– время колебательного процесса, T > 0 – время моделирования. Если в уравнении (1) функции памяти имеют степенную зависимость от времени вида
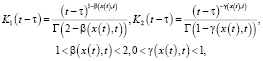(2)
то интегро-дифференциальное уравнение (1) можно записать в терминах производных дробных переменных порядков:
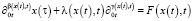, (3)
где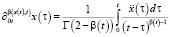 
, 
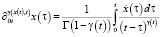– операторы дробного дифференцирования переменных порядков.
Существует другое представление операторов дробных производных, например, если степенные функции (2) имеют вид
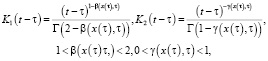(4)
тогда уравнение (3) запишется несколько иначе:
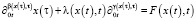, (5)
где
, 
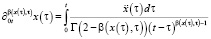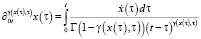– операторы дробного дифференцирования.
Уравнения (3) и (5) описывают класс эредитарных нелинейных колебательных систем, и они будут являться в дальнейшем объектами нашего исследования. Для уравнений (3) и (5) справедливы начальные условия вида
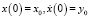. (6)
Задачи Коши (3), (6) и (5), (6) будем решать с помощью теории конечно-разностных схем [10]. Рассмотрим некоторые варианты аппроксимации операторов дробного дифференцирования, входящих в уравнения (3) и (5). Для этого рассмотрим равномерную расчетную сетку и разобьем отрезок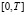 
на N частей с постоянным шагом τ при этом 
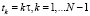. Введем сеточную функцию 
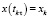. Согласно работах [8, 24], такую аппроксимацию можно осуществить с помощью следующих формул для операторов из уравнения (3):
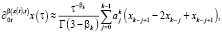
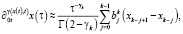(7)
где весовые коэффициенты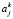 
и 
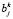определяются по формулам
, 
.
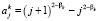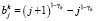Для операторов из уравнения (5):
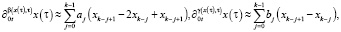(8)
где весовые коэффициенты aj и bj имеют вид
, 
.
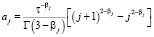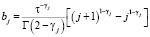Можно показать, следуя методикам из работ [29] и [16], что аппроксимации операторов дробного дифференцирования (7) и (8) имеют первый порядок. Если необходимо аппроксимировать операторы дифференцирования со вторым порядком, то можно воспользоваться следующими модифицированными формулами трапеций [17]:
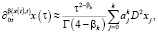
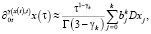(9)
где весовые коэффициенты уже будут определяться по формулам:
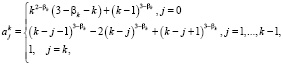
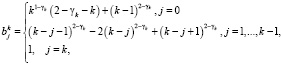
а D2xj и Dxj – дифференциальные операторы для второй и первой производных. Для значений xj, где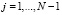 
эти операторы можно аппроксимировать со вторым порядком известными формулами центральных разностей:
.
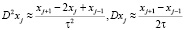Рассмотрим более подробно аппроксимацию в точке x0 для оператора D2x0, та как не задано дополнительного начального условия для второй производной при t = 0, то можно его аппроксимировать разностной формулой вида
,
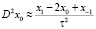где узел x–1 будет являться фиктивным и определяется согласно второму начальному условию (6) по формуле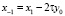 
. В итоге соотношения (9) можно переписать следующим образом:
(10)
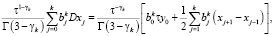
где y0 = Dx0 следует из начальных условий (6).
Аналогично мы можем рассмотреть аппроксимацию для дифференциальных операторов дробных производных, входящих в уравнение (5):
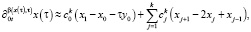(11)
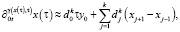
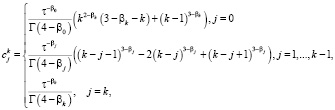
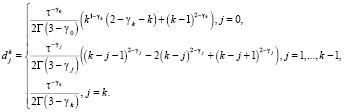
Отметим, что можно построить аппроксимации операторов дробных производных более высокого порядка. Например, по обобщенным формулам Симпсона [17]. В этой работе мы с помощью аппроксимаций (7)–(11) построим и исследуем соответствующие конечно-разностные схемы для дифференциальных задач (3), (6) и (5), (6) в зависимости от вида функци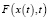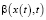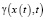й 
, 
, 
и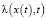 
, а также значений управляющих параметров. С помощью конечно-разностных схем построим и исследуем осциллограммы и фазовые траектории эредитарных нелинейных осцилляторов.
Необходимо отметить, что аппроксимации (9) и (11) имеют второй порядок, поэтому построенные на их основе конечно-разностные схемы должны иметь также второй порядок аппроксимации. Однако, если аппроксимация в граничных точках имеет первый порядок, то конечно-разностная схема в итоге будет иметь первый порядок аппроксимации. Для повышения порядка аппроксимации конечно-разностной схемы необходимо использовать специальные методики аппроксимации в граничных точках, например метод фиктивного узла. Нас не будет интересовать более высокий, чем первый, порядок аппроксимации конечно-разностных схем.
Эредитарный осциллятор Дуффинга
Рассмотрим типичный нелинейный осциллятор Дуффинга [12], но с учетом эредитарности. В этом случае для эредитарного осциллятора Дуффинга в уравнении (1) положим: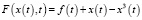 
и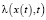 
является постоянной функцией. Здесь функция f(t) – внешнее воздействие на колебательную систему, как правило гармоническая функция.
Отметим, что в работе [28] был рассмотрен эредитарный осциллятор Дуффинга с фрактальным трением с дробной производной Римана – Лиувилля. Такой осциллятор использовался для изучения вязкоупругих свойств пучков, пластин и цилиндрических оболочек в работе [26], а также в работе [19] для организации и настройки PID контроллера. В работах [1] и [2] проведено обобщение модели осциллятора Дуффинга с фрактальным трением, построены осциллограммы и фазовые траектории для этой колебательной системы, получены новые колебательные режимы и подтверждены результаты работы [12]. В работе [5] была предложена математическая модель эредитарного осциллятора Дуффинга с производными дробных постоянных порядков в смысле Герасимова – Капуто, а в работе [6] была обобщена на случай переменных дробных порядков. Рассмотрим пример.
Пример 1. Управляющие параметры для эредитарного осциллятора Дуффинга выберем следующими: β(t) = 1,6 – 0,001t, γ(t) = 0,7 – 0,005t, f(t) = δcos(ωt), δ = 20, ω = 1, λ = 0,3, х0 = 0,2, y0 = 0,1. На рис. 1 приведены осциллограмма (рис. 1, а) и фазовая траектория (рис. 1, б), полученная для примера 1 при N = 2000 и T = 100 с помощью одной из конечно-разностных схем, на основе аппроксимаций (7)–(11).
Из рис. 1 мы можем увидеть, что амплитуда колебаний (рис. 1, а) имеет установившийся характер. Также можно заметить некоторое раздвоение колебаний на минимумах и максимумах, что на фазовой траектории (рис. 1, б) соответствует симметричным петлям. Фазовая траектория (рис. 1, б) выходит на предельный цикл, так, как колебания, не затухающие с установившейся амплитудой.
Эредитарный осциллятор Ван дер Поля
Рассмотрим другой тип эредитарного осциллятора – эредитарный осциллятор Ван дер Поля, который характеризует автоколебания. Для этого в исходных уравнениях (3) и (5) надо положить: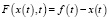 
, 
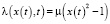, где μ – коэффициент, который характеризует нелинейность в силу затухания колебаний.
Эредитарный осциллятор Ван дер Поля с производной дробного переменного порядка в диссипативной составляющей рассматривался в работе [13] с целью изучения вязкоупругих свойств осциллятора. В работе [7] автором была предложена математическая модель эредитарного осциллятора Ван дер Поля с производными дробных постоянных порядков в смысле Герасимова – Капуто. Рассмотрим пример.
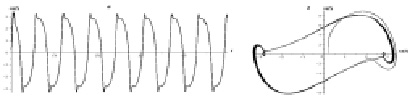
Рис. 1. Осциллограмма (а) и фазовая траектория (б) для примера 1
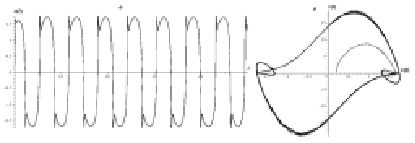
Рис. 2. Осцилляторы (а) и фазовые траектории (б) для примера 3
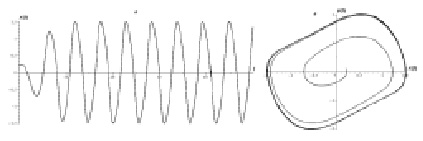
Рис. 3. Осциллограмма (а) и фазовая траектория (б)
Пример 2. Управляющие параметры для эредитарного осциллятора Ван дер Поля выберем следующими: β(t) = 1,8 – 0,001cos(πt), γ(t) = 0,7 – 0,005sin(πt), f(t) = δcos(ωt), δ = 20, ω = 1, μ = 12, х0 = 0,2, y0 = 0,1. На рис. 3 приведены осциллограмма (рис. 2, а) и фазовая траектория (рис. 2, б) для этого примера при значениях N = 2000 и T = 100.
Из рис. 2 видно, что осциллограмма (рис. 2, а) и фазовая траектория (рис. 2, б) похожи на осциллограмму (рис. 1, а) и фазовую траекторию (рис. 1, б) для эредитарного осциллятора Дуффинга. Поэтому можно сделать вывод о том, что введение производных с переменными дробными порядками в исходное уравнение осциллятора дает возможность получить колебательные режимы присущие другим осцилляторам.
Пример 3. Управляющие параметры: β(t) = 1,8 – 0,003sin(t), γ(t) = 0,8 – 0,005sin(t), f(t) = δcos(ωt), δ = 0, ω = 1, μ = 1, х0 = 0,2, y0 = 0,1. На рис. 3 приведены осциллограмма и фазовые траектории для этого примера.
Обратим внимание, что в примере 3 функция f(t) = 0. Амплитуда колебаний (рис. 3, а) со временем выходит на постоянный уровень, а фазовая траектория (рис. 3, б) стремится к аттрактору. Отметим, что введение производных дробных порядков в осцилляционное уравнение с нулевой правой частью приводит к затуханию колебаний. Это было показано в работе [11], где для эредитарного осциллятора в законе полной механической энергии появляются члены, которые отвечают за диссипацию энергии. В этом примере вы видим отсутствие диссипации энергии при нулевой правой части.
Эредитарный осциллятор с учетом stick-slip эффекта
Рассмотрим нелинейный осциллятор, который характеризует эффект прилипания скольжения и исследуется в рамках теории трибологии. С помощью этого осциллятора можно, например, описать латеральное движения груза по поверхности электронного атомного микроскопа [9] или использовать его в качестве механической модели землетрясений [30]. В этом случае в правой части уравнений (3) и (5) находится функция
,
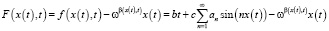где b – скорость движения груза вдоль поверхности, с – энергия адгезии поверхности,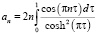 
– коэффициенты ряда Фурье. В работе [9] указывается, что для расчета достаточно взять следующие семь коэффициентов Фурье: a1 = 0,436, a2 = 0,344, a3 = 0,164, a4 = 0,058, a5 = 0,021, a6 = 0,004, a7 = 0,003. Рассмотрим некоторые примеры.
Пример 4. Управляющие параметры для эредитарного осциллятора с эффектом stick-slip выберем следующими:
β(t) = 1,8 – 0,003sin(t), γ(t) = 0,8 – 0,005sin(t), b = 1, δ = 50, ω = 1, λ = 0,3, х0 = 0,2, y0 = 0,1. На рис. 4 приведена осциллограмма и фазовые траектории, полученные по одной из схем на основе аппроксимаций (7)–(11).
На рис. 4 видны две потенциальные ямы, в которых груз начинает прилипать вследствие адгезии поверхности, далее виден срыв груза в результате груз начинает скользить, испытывая колебания.
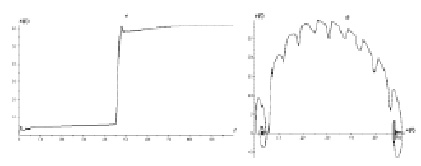
Рис. 4. Осциллограмма (а) и фазовая траектория (б) для примера 4
Результаты исследования и их обсуждение
Численный анализ нелинейных осцилляторов показал, что при определенных значениях управляющих параметров и функциональных зависимостей дробных показателей β(t) и γ(t) могут появляться колебательные режимы, которые присущи другим нелинейным осцилляторам. Для эредитарного осциллятора Ван дер Поля, совершающего свободные колебания, были получены осциллограмма и фазовая траектория, которые соответствуют незатухающим колебаниям. Это является важным результатом, так как ранее считалось, что введение дробных производных в осцилляционные уравнения приводит к диссипации энергии колебательной системы [11].
Дальнейшее продолжение работы – качественный анализ решений нелинейных эредитарных осцилляторов, построение карт динамических режимов, показателей Ляпунова и сечений Пуанкаре, а также определение и классификация точек покоя.
Библиографическая ссылка
Паровик Р.И. ДРОБНОЕ ИСЧИСЛЕНИЕ В ТЕОРИИ КОЛЕБАТЕЛЬНЫХ СИСТЕМ // Современные наукоемкие технологии. – 2017. – № 1. – С. 61-68;URL: https://top-technologies.ru/ru/article/view?id=36557 (дата обращения: 24.11.2024).