Появление новых материалов и композитов диктует развитие норм по проектированию конструкций, а также приводит к необходимости более широкого использования компьютерных технологий для оценки их надёжности и прогнозирования работы в условиях, приближённых к эксплуатационным [1–5], что способствует развитию методов имитационного моделирования. В настоящее время предложен ряд детерминированных и вероятностных алгоритмов на основе математической нелинейно-деформационной модели, позволяющей прогнозировать надежность изгибаемых элементов дисперсной структуры, армированных дискретными волокнами. Данные алгоритмы использованы при создании программы для ЭВМ по оценке надежности фибробетонных балок, работающих на изгиб, с учетом физической нелинейности материалов «SFRC.exe» (свидетельство о государственной регистрации программы для ЭВМ № 2016611439). Вероятностный расчет состоит в определении статистических характеристик прочности, жесткости и трещиностойкости исследуемых элементов конструкции при проведении большого количества статистических испытаний, связанных с моделированием исходных случайных величин. Для определения этих характеристик на каждом этапе разыгрываний проводится детерминированный расчет по нелинейно-деформационной модели, который положен в основу вероятностного алгоритма. Результатом работы программы являются показатели надежности изгибаемых элементов, армированных стальными дискретными волокнами, по прочности, жесткости и трещиностойкости. Данные показатели позволяют судить об эксплуатационной пригодности исследуемых элементов конструкций. Блок-схемы алгоритмов программы представлены в работах [6, 7].
Для анализа основных статистических характеристик материалов использовался большой объем информации по обработке экспериментальных данных, полученных в лабораториях кафедр общей механики и строительных материалов ЛГТУ [6, 7].
Разработанный на основе детерминированной и вероятностной моделей программный комплекс «SFRC.exe» предназначен для анализа напряженно-деформированного состояния в нормальном сечении изгибаемого элемента и оценки надежности элементов, работающих на изгиб. Программа позволяет учитывать различные сочетания прочностных характеристик матрицы композита, объемного содержания дискретных волокон и их ориентации.
Структура программной среды на уровне информационного взаимодействия состоит из следующих основных модулей:
IZGIB – управляющий модуль, через который производится обращение к другим вспомогательным обеспечивающим модулям; необходим для вычисления изгибающего момента и прогибов балок прямоугольного сечения, лежащих на двух опорах.
К обеспечивающим модулям относятся:
1. Модуль DIAG – подпрограмма расчета диаграмм деформирования матрицы по заданным физико-механическим характеристикам. Алгоритм расчета напряженно-деформированного состояния изгибаемого элемента приведен в работе [7]. В работе [9] приведены основные аналитические зависимости для расчета напряжений в нормальном сечении элемента с волокнистой структурой (фибробетонов и сталефибробетонов). Данный модуль содержит подпрограммы, позволяющие рассчитывать напряженно-деформированное состояние элемента как в случае изотропной структуры (без дискретных волокон), так и в случае наличия анизотропной структуры (наличие ориентированных или дисперсно-распределенных по объему дискретных волокон, – стальной фибры).
2. Модуль FIBER – подпрограмма, генерирующая случайное распределение дискретных волокон в матрице композита. Основными входными параметрами для построения дисперсной структуры нормального сечения изгибаемого элемента являются геометрические характеристики сечения (высота, ширина) и объёмное содержание фибровой арматуры в объёме исследуемого образца. Модуль позволяет анализировать характер распределения волокон в нормальном сечении, а также их геометрические характеристики, – углы ориентации и заделку.
3. Модуль GEOM – подпрограмма построения геометрической структуры дисперсного элемента с дискретными волокнами по всему объему.
4. Модуль NAD – модуль расчета надежности элементов на основе вероятностной математической модели. Основные стохастические характеристики, необходимые для оценки надёжности исследуемого изгибаемого элемента, и алгоритм вероятностной модели приведён в работе [6].
5. Модуль DETERM – на основе детерминированной математической модели осуществляет расчет напряженно-деформированного состояния изгибаемого элемента на каждой стадии нагружения. Алгоритм расчета приведён в работе [5, 7].
6. Модуль MF – осуществляет расчет координат диаграммы «изгибающий момент – прогиб», выводит на экран результаты вычислений.
Структурная схема, отражающая связи между модулями программного комплекса в процессе анализа НДС изгибаемых элементов, представлена на рис. 1.
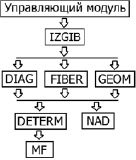
Рис. 1. Структурная схема алгоритма взаимодействия модулей программного комплекса «SFRC.exe»
Пользовательский интерфейс позволяет осуществить ввод следующих параметров:
– геометрические характеристики изгибаемого элемента (рис. 2);
– параметры дисперсного распределения дискретных волокон (рис. 3).
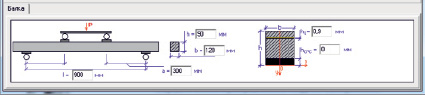
Рис. 2. Ввод геометрических характеристик изгибаемого элемента
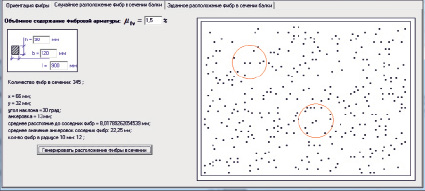
Рис. 3. Ввод и генерация параметров распределения дискретных волокон
В отдельных окнах программы производится вывод результатов расчета напряженно-деформированного состояния изгибаемого элемента с использованием детерминированного алгоритма (рис. 4) и вероятностного алгоритма (рис. 5). Заметим, что результатом расчета изгибаемого элемента по вероятностной модели является таблица с показателями надежности исследуемого образца с заданными геометрическими и физико-механическими характеристиками. Надежность образца оценивается по трем основным критериям: трещиностойкость (ширина раскрытия трещины в опасном нормальном сечении образца), жесткости (прогиб в центральном сечении) и прочности (максимальная нагрузка, при которой образец не разрушается).
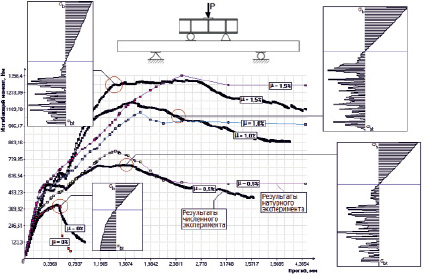
Рис. 4. Вывод результатов численного и натурного экспериментов для образцов-балок 120×90×1560 мм (детерминированный алгоритм)
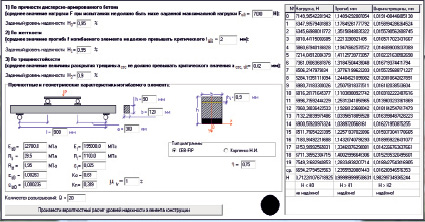
Рис. 5. Вывод показателей надежности и таблицы результатов, полученных с использованием вероятностного алгоритма
На рис. 4 в окне программы также показано сравнение результатов натурных экспериментов со значениями численных экспериментов, полученных с помощью программы «SFRC.exe» для образцов-балок с объемным армированием mfv = 0, 0,5, 1,0 и 1,5 % [9].
Среднеквадратичное отклонение результатов (изгибающий момент) численного эксперимента от результатов натурного эксперимента составило:
– для образцов с объемным армированием mfv = 0 % –7,225 Нм;
– для образцов с объемным армированием mfv = 0,5 % – 11,475 Нм;
– для образцов с объемным армированием mfv = 1,0 % – 21,574 Нм;
– для образцов с объемным армированием mfv = 1,5 % – 26,007 Нм.
В таблице показаны результаты апробации программного комплекса, полученные при оценке надежности брусковых перемычек, изготовленных из бетонов на предприятии ОАО «Завод Железобетон» г. Липецка. Прогибы опытных балок от действия кратковременной нагрузки определяли двумя способами [10]:
– непосредственным замером при помощи индикаторов-прогибомеров;
– используя опытное значение кривизны в середине пролета балки по формуле
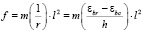 , (1)
, (1)
где m – коэффициент, зависящий от условий опирания и схемы загружения, принятый в данном случае 0,106; l = 900 мм – пролёт балки; h = 90 мм – высота сечения балки; εbr и εbc – относительные деформации на уровне растянутой и сжатой грани сечения; 1/r – радиус кривизны балки.
Результаты апробации программного комплекса
|
Марка образца |
Требуемые уровни надежности |
Требуемые критерии пригодности |
Оценка надежности по вероятностной математической модели |
||||
|
Н0 |
Н1 |
Н2 |
Н0 |
Н1 |
Н2 |
||
|
БШ-1 |
0,95 |
0,95 |
0,9 |
Fult = 7 кН, fult = 2 мм, acrc,ult = 0,02 мм |
0,7 (не надежно) |
0,99 (надежно) |
0,98 (надежно) |
|
БО-1 |
0,95 |
0,95 |
0,9 |
0,98 (надежно) |
0,99 (надежно) |
0,94 (надежно) |
|
|
ФБО-1-0,5 |
0,93 |
0,95 |
0,9 |
Fult = 7,5 кН, fult = 2,2 мм, acrc,ult = 0,02 мм |
0,94 (надежно) |
0,95 (надежно) |
0,97 (надежно) |
|
ФБО-1-1,0 |
0,93 |
0,92 |
0,8 |
Fult = 8 кН, fult = 2,4 мм, acrc,ult =0,015мм |
0,94 (надежно) |
0,91 (не надежно) |
0,73 (не надежно) |
|
ФБО-1-1,5 |
0,9 |
0,90 |
0,8 |
Fult = 9 кН, fult = 2,8 мм, acrc,ult = 0,01 мм |
0,92 (надежно) |
0,94 (надежно) |
0,74 (не надежно) |
На основании данных численных и натурных экспериментов предложены рекомендации по применению имитационных математических моделей для оценки начальной надежности изгибаемых элементов дисперсной структуры с помощью созданного на основе описанных алгоритмов программного комплекса «SFRC.exe».
Для применения программного комплекса «SFRC.exe» необходима информация о законах распределения и средних значениях (математических ожиданиях), среднеквадратических отклонениях или дисперсиях тех случайных величин, которые являются входными параметрами для исследования изгибаемого элемента с дискретными волокнами (бетона или фибробетона) в эксплуатационных условиях. Как правило, принято считать их распределение подчиненным нормальному закону, что подтверждается статистическим анализом большого массива технологических параметров [11]. Определение статистических параметров таких показателей производится по результатам генеральной совокупности с использованием интервальной оценки на базе накопленной априорной информации по всем необходимым показателям. Определение стохастических характеристик согласно стандарту ГОСТ 11.006-74, ГОСТ 21013-86 предусматривает проверку нормальности распределения исследуемой характеристики, расчет стационарных выборочных оценок для дисперсии и математического ожидания, проверку однородности дисперсии, а также определение по мере накопления информации характеристик априорного распределения. Ежесменная автоматизированная оценка эксплуатационной пригодности изгибаемых элементов конструкций с дискретными волокнами (бетонов или фибробетонов) реализуется посредством передачи программному комплексу характеристик необходимых для расчёта параметров, изменчивость которых может оказать значительное влияние на надежность исследуемой конструкции.
Библиографическая ссылка
Корнеев А.М., Бузина О.П., Суханов А.В. ПРОГРАММНЫЙ КОМПЛЕКС ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ПРОЦЕССА ИЗМЕНЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ НЕОДНОРОДНЫХ АНИЗОТРОПНЫХ ОБЪЕКТОВ // Современные наукоемкие технологии. 2017. № 1. С. 41-45;URL: https://top-technologies.ru/ru/article/view?id=36553 (дата обращения: 13.03.2026).



