Задачей электроимпедансной томографии (ЭИТ) является получение информации о распределении проводимости в объеме рассматриваемого биологического объекта. Методика проведения ЭИТ заключается в последовательной подаче токовых импульсов на различные пары электродов и снятие значений потенциалов относительно заземленного электрода на всех остальных. Полученные значения потенциалов используются для решения обратной задачи, с помощью которой для каждой пары токовых электродов приближенно восстанавливают картины распределения проводимостей, называемые проекциями. Затем проекции усредняются.
Многочастотная ЭИТ основана на использовании нелинейной зависимости проводимости σ и диэлектрической проницаемости ε биологических тканей от частоты инжектируемого тока, что позволяет получать дополнительную информацию, например оценить соотношение внутриклеточной и межклеточной жидкостей.
Цель исследования
Целью исследования является оценка возможности применения математической модели стационарных токов для решения обратной задачи реконструкции проводимости биологического объекта для многочастотной ЭИТ.
Материалы и методы исследования
Для достижения поставленной цели была разработана методика, заключающаяся в решении серии модельных прямых задач расчета распределения плотности тока для интересующего диапазона частот инжектируемого гармонического тока с использованием стационарной и символической математических моделей поля с последующим сравнением значений амплитуд потенциалов на измерительных электродах. Методика основана на применении численных методов решения полевых задач. В работе используются математические модели электромагнитного поля в виде программного пакета конечноэлементного анализа Femm 4.2, а также модели, описывающие зависимость электрических параметров биологических тканей от частоты инжектируемого тока.
Модель живой клетки
Зависимость параметров σ и ε от частоты инжектируемого тока вызвана сложной неоднородной структурой ткани, состоящей из клеток. Эквивалентную электрическую схему живой клетки можно представить в виде участка электрической цепи, состоящей из трех элементов: внутреннего сопротивления клетки Ri, сопротивления межклеточной жидкости Re и емкости мембран Cm (рис. 1, а) [2]. Здесь под Cm понимается емкость системы из двух мембран, через которые ток проходит последовательно, то есть Cm = Cмембр/2, где Cмембр – характеристика клеточной мембраны. Следует отметить, что существуют и другие схемы замещения [5], отражающие неоднородную внутреннюю структуру клетки с различной степенью точности.
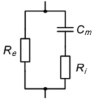
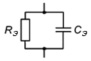
а) б)
Рис. 1. Электрические схемы замещения живой клетки
Для такой электрической схемы может быть определен импеданс [2]
,
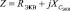где
,
,
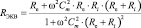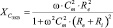ω – угловая частота, связанная с частотой f инжектируемого тока согласно формуле f = 2πω. Данная аппроксимация зависимости эквивалентных электрических интегральных параметров биологического объекта успешно используется для оценки соотношения объемов внутриклеточной и межклеточной жидкостей.
Аналогичные формулы могут быть получены и для локальных параметров – проводимости σ и диэлектрической проницаемости ε. Их удобно объединить в обобщенную локальную характеристику
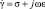, (1)
называемую комплексной проводимостью. Здесь j – мнимая единица.
Формуле для комплексной проводимости, имеющей действительную и мнимую части, соответствует эквивалентная схема замещения, представленная на рис. 1, б. Здесь два элемента, активное сопротивление RЭ и емкость СЭ, соединены параллельно. Им соответствуют удельная проводимость σ и диэлектрическая проницаемость ε при условии, что рассматриваемая электрическая цепь приходится на единицу длины вдоль линии тока, то есть RЭ и СЭ являются удельными параметрами. В этом случае будут справедливы зависимости
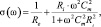(2)
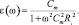(3)
Здесь значения Ri, Rе и Cm следует также рассматривать, как удельные усредненные параметры ткани.
Математическая модель электромагнитного поля
Важнейшей составляющей метода ЭИТ является обратная задача реконструкции распределения удельных электрических характеристик в объеме исследуемого биологического объекта. Существенное влияние на результат такой реконструкции оказывает выбор математической модели электромагнитного поля. В общем случае оно описывается уравнениями Максвелла (в дифференциальной форме) [4]:
, 
,
, 
, 
, 
, 
,
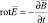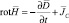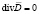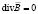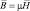где 
– напряженность электрического поля,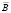 
– магнитная индукция, 
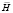– напряженность магнитного поля, 
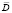– вектор электрического смещения, 
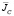– плотность наводимых полем токов проводимости, μ – магнитная проницаемость, t – время. Здесь учтено, что в области исследуемого объекта свободные заряды отсутствуют.
При инжектировании гармонического тока, изменяющегося по синусоидальному закону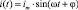 
, где im – амплитуда тока, φ – фаза, которую можно положить для тока источника равной нулю, а также при условии снятия измерений после окончания переходных процессов можно использовать уравнения Максвелла в символической форме:
, 
,
, 
, 
, 
, 
,
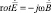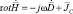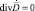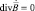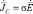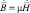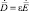где точка над символом означает, что число является комплексным и содержит информацию об амплитуде величины и сдвиге фаз относительно инжектируемого тока источника.
В этом случае можно ввести комплексный скалярный электрический потенциал:
,
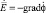а система уравнений Максвелла может быть сведена к одному уравнению:
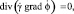(4)
где 
– комплексная удельная проводимость, определяемая согласно формуле (1).
В простейшем приближении процесс растекания токов в объеме биологического объекта считают стационарным, полагая все производные по времени равными нулю. В этом случае система уравнений Максвелла сводится к одному уравнению относительно скалярного электрического потенциала ?:
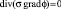. (5)
Оценка применимости стационарной математической модели для реконструкции проводимости биологического объекта
Уравнение (4) отличается от уравнения (5) добавочным слагаемым jωε у множителя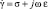 
. Видно, что величина этого слагаемого зависит от частоты зондирующего гармонического тока и от диэлектрической проницаемости ткани.
Было проведено исследование влияния этих параметров на результат реконструкции. Методика исследования основана на проведении численных экспериментов, заключающихся в решении ряда прямых задач расчета поля для синусоидальных токов разных частот и стационарной модели. Исходными данными для решения задачи реконструкции характеристик биологического объекта являются значения потенциалов на электродах. При использовании стационарной модели измеряют амплитуды сигнала, при использовании символической необходимо знать еще и смещение напряжения относительно зондирующего тока, то есть использовать фазочувствительный вольтметр [1].
Методика проведения численных экспериментов заключается в следующем:
1. Выполняется расчет прямой задачи на основе уравнения (4) для зондирующих токов интересующего диапазона частот.
2. Для таких же параметров среды выполняется расчет поля с использованием стационарной модели (5).
3. На каждом электроде модуль значения потенциала, полученного в результате решения задачи с использованием стационарной модели, сравнивается с амплитудами синусоидальных функций потенциала для каждой частоты.
4. Если для интересующей частоты полученное на шаге 3 расхождение не превышает заданный параметр е, определяемый требованиями к точности решения, то стационарная математическая модель (4) может быть использована для данной частоты.
Методика основана на том очевидном факте, что необходимым условием корректной работы алгоритма решения обратной задачи с использованием стационарной модели будет являться требование незначительного отклонения амплитуд потенциалов, полученных на электродах при использовании ее и более точной символической модели. Подобный подход, основанный на сравнении значений потенциалов на электродах, был применен для оценки схемы сканирования в [3] для трехмерной электроимпедансной маммографии.
Результаты исследования и их обсуждение
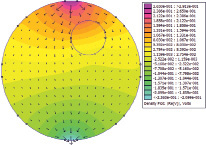
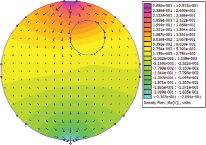
Для иллюстрирования предлагаемой методики были проведены численные эксперименты с использованием программного пакета конечноэлементного анализа Femm 4.2. Рассматривалась модельная плоскопараллельная задача с областью расчета D0 в виде круга диаметром 17 см, включающая одну неоднородность D1 – круг диаметром 4,2 см (рис. 2). К границам области было приложено 8 равноотстоящих электродов. Ток силой 1 мА инжектировался через верхний и нижний электроды. В качестве общего электрода, в котором значение потенциала принято равным нулю, был выбран правый.
|
а) |
б) |
Рис. 2. Область расчета для частоты 50 кГц: модели 5 (а) и 4 (б)
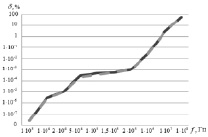
На рис. 3, а показана зависимость расхождения значений амплитуд потенциалов от частоты при параметрах: значения удельных проводимостей σ0 = 0,5 См/м, σ0 = 10–6 См/м, значения относительных диэлектрических проницаемостей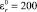 
, 
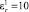. Расхождение значений амплитуд потенциалов оценивалось по формулам
,
,
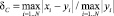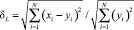где N = 8 – количество электродов, а в качестве xi и yi брались значения амплитуд потенциалов на i-м электроде при частотах f и 0 Гц соответственно. График подтверждает увеличение величины расхождения с ростом частоты, однако для таких малых значений диэлектрической проницаемости оно несущественно в диапазоне частот, применяемом в ЭИТ.
|
а) |
б) |
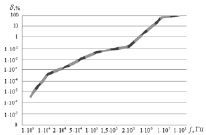
Рис. 3. Графики зависимости величины расхождения амплитуды потенциалов на электродах от частоты инжектируемого тока. Сплошной линией 
обозначена зависимость δC(f), пунктиром 
– δL(f)
Во втором опыте значение диэлектрической проницаемости области D1 было изменено: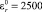 
. Значение расхождения потенциалов при этом увеличилось (рис. 3, б). В третьем опыте было учтено, что электрические характеристики ткани зависят от частоты инжектирующего тока. Так, согласно данным, приведенным в [2], мышечная ткань имеет характеристики, представленные в таблице.
Значения относительной диэлектрической проницаемости для мышечной ткани при разных частотах (периодах) изменения зондирующего тока и полученные величины расхождения для амплитуд потенциалов на электродах
|
№ |
Период изменения инжектируемого тока τ, с |
Частота изменения инжектируемого тока f, Гц |
Относительная диэлектрическая проницаемость мышечной ткани εr |
Величина расхождения δC(f), % |
Величина расхождения δL(f), % |
|
1 |
2,274·10-3 |
440 |
2,5·107 |
36,71 |
36,71 |
|
2 |
3,183·10-4 |
3140 |
1,2·106 |
7,78 |
7,78 |
|
3 |
3,537·10-7 |
2,83·106 |
7000,0 |
58,67 |
58,66 |
|
4 |
7,234·10-12 |
1,38·1011 |
50,0 |
99,88 |
99,88 |
В соответствии с приведенными данными была изменена диэлектрическая проницаемость области D0, проводимость осталась без изменений. Результаты приведены в таблице. Как можно видеть, расхождение значений потенциалов на электродах для мышечной ткани велико даже для небольших частот, что затрудняет использование стационарной модели. Следует отметить, что диэлектрическая проницаемость других тканей на порядок меньше проницаемости мышечной [2], что улучшит ситуацию.
Выводы
Постановка обратной задачи многочастотной ЭИТ существенно зависит от математической модели, выбранной для описания растекания тока в исследуемом объекте. При использовании уравнений Максвелла в символической форме и модели (4) результатом решения обратной задачи для каждой проекции будет являться распределение комплексной проводимости, то есть в этом случае для каждой частоты будет известна как собственно проводимость σ, так и диэлектрическая проницаемость ε. Используя полученные значения σ и ε, можно решить систему нелинейных уравнений (2–3) и получить параметры ткани Ri, Re и Cm. При выборе стационарной модели (5), позволяющей быстрее решать обратную задачу по сравнению с моделью (4), возможно получить информацию лишь о действительной части комплексной проводимости, то есть получить картину собственно удельной проводимости σ. При этом информация о диэлектрической проницаемости ε будет потеряна. Тогда для восстановления параметров ткани Ri, Re и Cm можно будет использовать лишь выражение (2), что потребует для обеспечения такого же качества определения параметров выполнения измерений на большем количестве частот. Кроме того, область применимости стационарной модели ограничена. Оценить возможность применения стационарной модели для интересующей частоты изменения гармонического зондирующего тока возможно с помощью предложенной методики, решив для предполагаемой области две прямые задачи расчета распределения токов в области объекта и получив значения расхождений потенциалов на измерительных электродах.
Работы выполняются при поддержке Российского фонда фундаментальных исследований в рамках гранта «мол_а_дк» № 16-38-60173 «Технологии интеллектуального анализа данных электроимпедансной томографии для трехмерной реконструкции и визуализации проводимостей внутренних структур биологических объектов».
Библиографическая ссылка
Алексанян Г.К., Денисов П.А., Черноиван Д.Н. МЕТОДИКА ОЦЕНКИ ПРИМЕНИМОСТИ СТАЦИОНАРНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ЗАДАЧ МНОГОЧАСТОТНОЙ ЭЛЕКТРОИМПЕДАНСНОЙ ТОМОГРАФИИ // Современные наукоемкие технологии. – 2017. – № 1. – С. 7-11;URL: https://top-technologies.ru/ru/article/view?id=36547 (дата обращения: 22.11.2024).