Обоснованное назначение рациональных норм геометрической точности, характеризуемых допусками на размеры, допусками формы и расположения поверхностей применительно к изделиям машиностроительного производства, призвано обеспечить их качество и надежность, а также исключить излишние затраты на изготовление. Нормирование точности рационально сопровождать размерным анализом. Выполнение размерного анализа также необходимо при проектировании технологических процессов изготовления деталей с повышенными требованиями к геометрической точности, соизмеримой с точностью, обеспечиваемой оборудованием, а также при проектировании технологий сборки. Особенно актуален размерный анализ для новых образцов техники, для проектирования которой отсутствуют стандарты, руководящие документы и другая информация, позволяющая обоснованно осуществлять нормирование точности. В современных CAD/CAM/CAE системах имеются инструментальные средства размерного анализа, позволяющие осуществлять расчет размерных цепей, как методом полной взаимозаменяемости, так и вероятностным методом, но результаты расчета не влияют на геометрию моделей, выполненных по номинальным размерам. Инструментальные средства размерного анализа часто не доступны пользователям в той комплектации программных продуктов, которыми располагают предприятия или учебные заведения. Например, в академической версии NX 8.5 и далее инструмент расчета размерных цепей отсутствует. В версии 8 он дает некорректные значения и служит, вероятнее всего, только для ознакомления. Тем не менее с задачами решения размерных цепей периодически приходится сталкиваться, и в данной статье предлагается подход к решению размерных цепей с привлечением электронных таблиц, сопровождающих модели.
Для гиперболоидных передач (рис. 1) отсутствуют стандарты, нормирующие их точность. По аналогии с другими типами зубчатых передач, например, такими как конические, гипоидные, необходимо выявить показатели норм кинематической точности, плавности хода и пятна контакта [1, 2], обеспечивающие работоспособность передачи при закладываемых в конструкцию показателях надежности. Числовые показатели точности передачи могут определяться по аналогии.

Рис. 1. Модель редуктора с гиперболоидными зубчатыми колесами
Необходимо также корректно назначить нормы точности деталей передачи, таких как валы, корпусные детали и другие, обеспечивающие правильное относительное расположение делительных гиперболоидов (рис. 2).

Рис. 2. Совмещение делительных гиперболоидов зубчатых колес, участвующих в зацеплении. Красные линии – линии пересечения гиперболоидов; синие – горловые сечения делительных гиперболоидов
Анализ влияния отклонений на вышеназванные параметры желательно осуществлять с применением инструмента анализа по трехмерным моделям непосредственно в CAD/CAM/CAE системе. Данная работа выполнялась в системе NX, предоставляющей пользователю эффективный набор инструмента для анализа геометрических моделей.
Моделирование рационально вести в контексте сборки, для удобства контроля взаимного расположения деталей конструкции и выявления элементов конструкции, образующих размерные связи. При этом относительное расположение деталей задается с помощью сопряжений сборки, характерных для конструкции, выполненной в материале. Размеры элементов геометрии деталей, участвующих в размерных цепях, необходимо определять в качестве параметров конструкции. Данные параметры удобнее определить непосредственно в сборке, откуда они могут быть считаны непосредственно в файлы деталей и учтены в качестве размеров их элементов геометрии. Моделирование деталей требуется осуществлять таким образом, чтобы непосредственно учитывалась специфика простановки размеров на модели или чертеже каждой детали и данные размеры непосредственно обеспечивали точность замыкающего звена в размерной цепи [7]. Например, для детали вал-шестерня (рис. 3) моделирование начинается с моделирования зубчатого колеса. Затем моделируется цилиндр, имеющий максимальный диаметр шейки вала и длину А6, начало цилиндра смещено влево на расстояние А1 + А2. Цилиндр логически объединяется с зубчатым колесом. Затем моделируются проточки, расположение которых соотносится с соответствующими торцовыми поверхностями модели, но ни их положение, ни размеры не влияют на рассматриваемую размерную цепь.
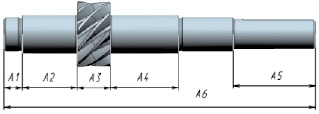
Рис. 3. Соотнесение параметров конструкции с размерами геометрических элементов модели
Используются традиционные методы нормирования точности в параметрах моделей. Например, метод равных допусков, метод равной точности [8], если значение допуска на замыкающее звено задается из условий работоспособности или собираемости конструкции. Назначаются верхние и нижние предельные отклонения на каждый размер каждого геометрического элемента всех моделей деталей, участвующих в сборочной размерной цепи. В сборке вводится параметр – «Замыкающее звено», числовое значение которого определяется измерением на модели, например это межцентровое расстояние между горловыми сечениями делительных гиперболоидов или осевой зазор в подшипниковом узле. Далее осуществляется вход в электронную таблицу, представляющую данные электронной модели. В надстройках осуществляется выделение выражений. Далее поочередно анализируется влияние каждого размера на замыкающее звено, добавлением к номинальному значению размера одного из предельных отклонений. После обновления модели результат замера значения замыкающего звена, отраженный непосредственно в электронной таблице, анализируется. Выявляется, какие из звеньев размерной цепи являются увеличивающими, а какие – уменьшающими. Далее значениям звеньев присваиваются поочередно такие, которые обеспечат получение максимального и минимального значения замыкающего звена. При данных сочетаниях размеров конструкция анализируется инструментальными средствами анализа геометрии (Измерения, анализ зазоров и интерференций).
Для учета влияния «векторных» звеньев размерной цепи необходимо дополнительно предусматривать относительное позиционирование геометрических элементов деталей, связанных также с параметрами моделей, доступными для изменения в виде координат или размеров, и непосредственно векторных величин, вдоль которых будут осуществляться геометрические построения.
Для анализа влияния бокового зазора на собираемость и работоспособность передачи, по результатам расчета боковых поверхностей зуба моделируется геометрия, соответствующая впадине зуба (используется методика [4, 5]) (рис. 4). В случае необходимости, с учетом вносимых изменений в профиль образующей линии может быть получена геометрия профильно-модифицированного зуба [6]. Данные геометрические элементы могут тиражироваться как равномерным круговым массивом вокруг оси вращения зубчатого колеса, так и неравномерно, с моделированием погрешности шага, обусловленного, например, неточностью позиционирования заготовки по угловой координате при обработке на станке. Так как впадина моделировалась по номинальным результатам расчета боковых поверхностей, увеличение размера впадины для моделирования гарантированного бокового зазора осуществляется на основе применения инструмента синхронного моделирования – смещение боковых граней впадины вращением вокруг оси вращения зубчатого колеса на заданный угол.

Рис. 4. Модель впадины зуба и его тиражирование вдоль периферии зубчатого колеса
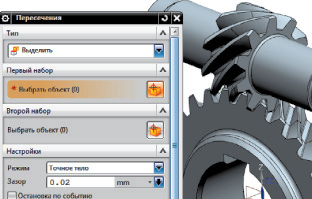
а

б
Рис. 5. а – диалог расчета «Пересечения» при моделировании работы зубчатых колес в зацеплении; б – полученная при наличии погрешностей форма пятна контакта
Анализ характера пятна контакта может осуществляться в приложении «Симуляция движения». Ведущему зубчатому колесу сообщается вращательное движение. Между зубчатыми колесами формируется 3D-контакт и предусматривается расчет «Пересечения», в том числе и при указании минимального значения зазора, гарантирующего наличие масляной пленки. На ведомом колесе моделируется нагрузка. При моделировании работы характер пятна контакта формируется в виде «тела пересечения» на поверхностях зубьев, при учете геометрических погрешностей, обусловленных неточностью изготовления и неточностью сборки (рис. 5).
Аналогичный подход может быть реализован для расчета размерных цепей, выполняемого при проектировании технологических процессов изготовления деталей, в том числе если пользователю предоставляется не мастер-модель детали, а ее ассоциативная копия. Размеры детали и исходной заготовки могут быть параметрически заданы на основе применения инструмента «синхронного моделирования». Если технология моделируется применительно к использованию станков с ЧПУ, то удобнее размеры модели выполнять по средним значениям и назначать на них симметричный допуск. В отличие от традиционного подхода, при котором необходимы геометрия готовой детали и исходной заготовки, между операциями формируется геометрия «Заготовки в процессе обработки», необходимо данную геометрию моделировать по параметрам, назначать допуски на все операционные размеры. Анализ будет осуществляться над «Припусками», являющимися замыкающими звеньями технологических размерных цепей [3].
Библиографическая ссылка
Абзалов А.Р., Иванова В.Н., Хабаров А.Е. РАЗМЕРНЫЙ АНАЛИЗ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ МОДЕЛЕЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ // Современные наукоемкие технологии. 2016. № 12-1. С. 9-13;URL: https://top-technologies.ru/ru/article/view?id=36467 (дата обращения: 04.03.2026).



