Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Насрулин Б.А. 1 Садех Нобари 1

---

1 АНО ВО «Университет Иннополис»

Графы являются распространенной структурой данных, которые нашли применение в различных областях, от явного применения в социальных сетях, а также неявных применений и в других сферах, таких как моделирование мозга человека. С одной стороны, необходимы гарантии конфиденциальности данных при публикации графов, с другой стороны, размеры графов постоянно растут, создавая необходимость в масштабируемых алгоритмах. Соединения в графе, а также индивидуальная информация являются основными данными в графе, нуждающиеся в конфиденциальности. Современные подходы для сохранения конфиденциальности, то есть метод L-непрозрачности, предлагают сильный метод конфиденциальности с учетом обезличивания связей в графе. Тем не менее из-за алгоритмической сложности это не представляется возможным для больших графов. В этой статье мы впервые проанализировали существующие решения для сохранения конфиденциальности связей в графах и работы по быстрой параллельной анонимизации графов. В результате мы предлагаем оптимизацию, которая использует GPU и обеспечивает масштабируемое решение. Основным ядром метода является вычисление всех кратчайших путей в графе, поэтому мы предложили два различных алгоритма, которые являются более эффективными, чем алгоритм Флойда – Уоршелла, с точки зрения используемой памяти и времени работы алгоритма. И, наконец, мы предлагаем две эвристики, которые существенно снижают вычислительную сложность, в то же время создавая меньшее количество искажений для исходного графа.

Статья в формате PDF

0 KB

графы

графические структуры

анонимизация графов

GPU

распределенные вычисления

1. Casas-Roma J., Herrera-Joancomart? J., Torra V. An algorithm for k-degree anonymity on large networks // Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. – ACM, 2013. – Р. 671–675.

2. Machanavajjhala A. et al. l-diversity: Privacy beyond k-anonymity // ACM Transactions on Knowledge Discovery from Data (TKDD). – 2007. – Т. 1, № 1. – Р. 3.

3. Nobari S. et al. L-opacity: Linkage-Aware Graph Anonymization // EDBT. – 2014. – Р. 583–594.

4. Narayanan A., Shmatikov V. How to break anonymity of the netflix prize dataset //arXiv preprint cs/0610105. – 2006.

5. Ying X., Wu X. On link privacy in randomizing social networks // Pacific-Asia Conference on Knowledge Discovery and Data Mining. – Springer Berlin Heidelberg, 2009. – Р. 28–39.

6. Yuan M. et al. Protecting sensitive labels in social network data anonymization // IEEE Transactions on Knowledge and Data Engineering. – 2013. – Т. 25, № 3. – Р. 633–647.

Публикация данных позволяет получить полезные данные, новое глубокое понимание данных и предложения по улучшению алгоритмов работы с этими данными. Социальные сети являются богатым набором данных, содержащим в себе информацию не только о личности пользователя, но и о его ближайшем окружении и их взаимоотношениях. К таким данным можно отнести обмены записей электронной почты, совместную работу в сети, обмен видео, изображений и т.д. Такие данные обычно моделируются в виде графа, который, при публикации, может предоставить ценную информацию в таких областях, как маркетинг, социология и выявление случаев мошенничества. Несмотря на ценность таких данных, публикация данного графа может нарушить конфиденциальность отдельных лиц. В настоящее время проводятся исследования о том, как уменьшить эти угрозы конфиденциальности, сохраняя при этом возможность публикации полезной информации [6]. Так, например, открытое соревнование на лучший алгоритм предсказания оценки фильмов «Netflix price» опубликовало данные отношений пользователей и фильмов в виде анонимизированного графа, в котором были изменены конфиденциальные данные пользователей. Однако структура графа может выявить конфиденциальную информацию, характеризующую пользователей. В работе [4] авторы использовали изоморфизм графа, сравнивая его с графом IMDB, что в итоге позволило рассекретить большинство участников графа.

Подобную утечку конфиденциальной информации может вызвать даже простая информация о структуре графа, такая как степень вершины, средняя длина пути и т.д. Такая деанонимизация возможна как и из-за простого сопоставления информации графа с социальной сетью (количество друзей), так и более сложного сопоставления, такого как k-изоморфизм. Результатом подобной утечки может стать факт раскрытия принадлежности к какой-либо группе вершин (сообщество), либо факт связи, отношений с определенной вершиной в графе (физическое лицо либо организация).

Последние публикации предлагают различные методы предотвращения подобных утечек [1]. Однако эти методы либо сильно разрушают структурную информацию о начальном графе, что уменьшает ценность подобной публикации, либо являются вычислительно неэффективными. Так, например, ни одна работа не учитывает особенности социальных сетей, таких как феномен «маленького мира» (Small world) или важность раскрытия связи коротких путей. Основную часть методов анонимизаций составляют работы, основанные на методе k-anonimity, с фокусировкой на анонимность вершин в социальной сети [2].

Ин и Ву [5] показывают, что топологическое сходство узлов может быть использовано для восстановления исходных соединений в графе. В работе также подтверждается, что даже если граф сохраняет вершинную анонимность, он не может сохранить анонимность ребер. В связи с этим они предлагают понятие конфиденциальности τ-confidence, что уменьшает уверенность противника в существовании некоторых ребер, используя эвристики для обмена и удаления ребер в графе.

В работе [3] авторы подробно рассмотрели проблему публикации графа с сохранением анонимности ребер в графе. Было показано, что предложенный метод значительно превосходит предыдущие методы по степени нанесения повреждений графу, сохраняя при этом анонимность ребер. Однако из-за алгоритмической сложности метода его невозможно применить на графы размерами больше чем 1000 ребер.

Формальная постановка задачи

В первую очередь мы предполагаем, что социальная сеть моделируется с помощью простого графа (т.е. неориентированный, невзвешенный граф, без самопересекающихся петель и кратных ребер). Пусть G (V, E) – простой граф, где V есть множество вершин и E – множество ребер в графе G. Степень dv вершины v∈V это количество ребер выходящих (или входящих) из вершины v. Для пары вершин, vi, vj, геодезическим расстоянием между ними с длиной l является кратчайший путь, соединяющий их.

Мы считаем, что каждая вершина характеризуется определенными свойствами, которые могут ее идентифицировать в опубликованном графе. Ради общности наш метод может защищать любое свойство графа. Такие свойства представляют интерес для злоумышленника и могут нести в себе угрозу конфиденциальности. Мы предполагаем что злоумышленник пытается определить человека по соответствующей вершине через степень вершины. Степень вершины формирует базовые знания злоумышленника. Степень вершины обычно является общедоступной информацией (количество друзей в социальной сети). Злоумышленник также может попытаться вывести длину связи между двумя конкретными лицами, что и является основным объектом анонимизации данного метода.

Определение 1. Пусть дан простой граф G и определено множество пар-вершин C. Каждая пара вершин vi, vj принадлежит максимум к одному типу, если между этими вершинами существует путь с длиной l_ij.

Определение 2. Пусть дан простой граф G и пара вершин типа T∈C, тогда L-непрозрачность типа Т определяется как отношение количества пар вершин с длиной не больше L к числу всех пар вершин в T, включая те, между которыми не существует путь.

.

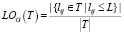Определение 3. Пусть дан граф G (V, E) и множество С типов пар вершин, тогда говорят что G удовлетворяет принципу L-непрозрачности относительно величины θ тогда и только тогда, если для каждой пары вершин Т, LOG(T ) не превышает величину q, то есть

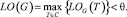
Для того чтобы измерить влияние алгоритма на оригинальный граф, мы ввели метрику искажения графа, которая является отношением количества ребер E’ измененного графа к количеству ребер в оригинальном графе E:

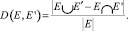
Задача 1. Пусть задан граф G(V, E), множество типов пар вершин C, параметры L и θ. Необходимо трансформировать оригинальный граф G(V, E) в граф G’(V, E’), который удовлетворяет условию L-непрозрачности относительно параметра θ так, чтобы величина искажения графа D(E, E’) была минимальной.

Вообще говоря, задача 1 является NP-полной. В работе [3] было приведено доказательство и вывод, что данная задача может быть решена с помощью приближений или эвристик. Однако эвристики, предложенные в данной работе, не предложили эффективный алгоритм работы с большими графами. Используемый алгоритм основан на алгоритме L-усеченного Флойда – Уоршелла для нахождения всех кратчайших путей, который рассчитывает все кратчайшие пути с длиной пути не более L. Однако на практике данный алгоритм работает хорошо лишь для больших значений L и для плотных графов. Для решения этой проблемы мы предложили эффективный распределенный алгоритм анонимизации графов на графическом процессоре.

Параллельный алгоритм L-непрозрачности

Алгоритм основан на жадной оптимизации, решая на каждом шагу, какое ребро удалить лучше всего. По данным матрицы путей и степеням вершин вычисляется матрица «непрозрачности» и возвращается максимальное значение этой матрицы, что и является характеристикой безопасности графа.

Каждая пара вершин (vi; vj) относится к одной паре вершин T_ij , представленной в виде пары степеней вершин (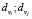). Пусть

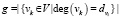
и

.

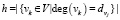Таким образом, каждый поток, соответствует одному ребру и записывает в 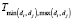величину 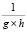, если 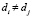, и величину 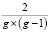, если 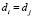. Простая имплементация данного алгоритма приведёт к ситуации гонки потоков, и в итоге результат не будет соответствовать реальному. Для решения этой проблемы мы использовали атомарные операции записи в матрицу.

Основным ядром вычисления является процесс вычисления кратчайших путей. Данная операция используется каждый раз при принятии решения удаления определенного ребра. Для уменьшения времени работы алгоритма вычисления всех кратчайших путей в работе была предложена оптимизация, которая вычисляет только кратчайшие пути с длиной не более заданной L. Несмотря на оптимизацию алгоритм работает очень медленно для больших графов (4 дня для графа с 10000 вершинами). Для ускорения вычисления в данной работе предложен параллельный алгоритм поиска в ширину c уровневой синхронизацией. Для реализации данного алгоритма мы использовали формат графа, представленного с помощью специальной разряженной матрицы (CSR). В данной матрице используются два массива: массив индексов и массив смежных вершин.

Основная идея алгоритма в том, что каждая вершина копирует всех соседей своих соседей на текущем уровне L, при этом не копируя данные (вершины), которые были ранее посещены. Другими словами, каждая вершина на каждом шагу расширяет свои границы.

Пусть AG(V, E),L – граф G(V, E) с множеством вершин V и ребер E, представленный с помощью разряженной матрицы, хранящей все пути длиной не более L.

Суть эффективного параллельного поиска в ширину заключается в следующем:

1. Формируется передняя граница для поиска в ширину. C = AG,l, если l = 1, это соответствует множеству всех кратчайших путей длиной 1. Для l = 2 все пути длиной 1 и 2, и т.д.

2. Для каждой пары вершин 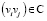параллельно выполняются шаги:

а) 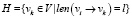, то есть все вершины, путь от которых до вершины vi, равен ровно l;

б)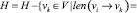

,

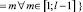обрезать все вершины, ранее посещенные вершиной vi;

в) .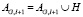

Эти шаги повторяются для всех значений .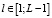

Одной из проблем реализации данного алгоритма является отсечение ранее посещенных вершин, так как трудно сказать заранее, была ли вершина посещена другой конкретной вершиной или нет. Одним из вариантов решения может быть копирование всех чисел, не принимая во внимание все ранее посещенные. Однако эта стратегия в конечном итоге приведет к нехватке памяти. Другая возможность состоит в том, чтобы скопировать только те вершины vj, которые не были ранее посещены текущей вершиной vi. Для реализации подобной обрезки можно использовать бинарный поиск. Другая возможность предполагает использование дополнительной |V|×|V| бинарной матрицы, представляющей из себя все посещенные вершины на текущем уровне L (L-БМ). Например, элемент vij в бинарном массиве представляет собой связь между вершиной vi и вершиной vj, и он равен единице, если соединение присутствует в пределах расстояния L, или ноль – в противном случае. Основной алгоритм принимает решение, какие ребра удалить так, чтобы граф G’ удовлетворял условиям метода L-непрозрачности.

Алгоритм L-непрозрачности

Основной алгоритм можно сформулировать в виде шагов:

Шаг 1. Рассчитать AG,L, используя алгоритм поиска всех кратчайших путей.

Шаг 2. Определить LO(AG,L), а также индекс матрицы T с максимальным значением.

Шаг 3. Индекс матрицы k можно однозначно представить в виде k = d×i + j, что соответствует паре степеней (di; dj).

Шаг 4. Паре степеней (di; dj) можно параллельно сопоставить V’ – множество пар вершин с (vi; vj) с длиной кратчайшего пути меньше чем L.

Шаг 5. Каждую пару вершин мы представляем в виде множества ребер составляющих путь от одной вершины до другой. Для уменьшения множества ребер, мы рассматриваем множество пересечений путей для данных вершин. Основная идея заключается в том, что если несколько путей пересекаются, то для того, чтобы разорвать наибольшее количество связей, нужно удалить ребра на пересечении. Такие ребра заносятся в множество E’.

Шаг 6. Каждое ребро из множества E’ проверяется с помощью параллельного алгоритма вычисления всех кратчайших путей. Мы удаляем такие ребра, что уменьшают максимальное значение в матрице T.

Шаги 2–6 повторяются до тех пор, пока для графа не будет выполняться LOG.

Эксперименты

Каждый из вышеприведенных алгоритмов был реализован на графическом процессоре GeForce GTX 980 4 Gb.

В табл. 1 приведены результаты работы метода L-непрозрачности с разными алгоритмами всех кратчайших путей. CPU-LFW соответствует алгоритму L-усеченного Флойда – Уоршелла, представленного в работе [3], реализованного на центральном процессоре. GPU-LFW представляет собой тот же алгоритм, реализованный на графическом процессоре, GPU-LBFS-BM является описанным выше алгоритмом, использующим дополнительный бинарный массив.

В результате численного эксперимента было установлено, что алгоритм, использующий множество параллельных поисков в ширину с бинарным массивом посещенных вершин, работает быстрее. Более того, алгоритм более оптимизирован для разряженных графов, используя меньше памяти, чем алгоритм Флойда – Уоршелла (CPU-FW, GPU-LFW). Кроме того, в табл. 2 представлены выкладки по нанесённым искажениям оригинальному графу в ходе работы метода.

Алгоритм, использующий множество параллельных поисков в ширину, использует в худшем случае такое же количество памяти, что и алгоритм Флойда – Уоршелла для больших величин L.

Таблица 1

Время работы метода L-непрозрачности с разными алгоритмами вычисления всех кратчайших путей графа G(V, E)

Таблица 2

Метрика искажения графа для методов L-непрозрачности с разными алгоритмами вычисления всех кратчайших путей графа G(V, E)

Выводы

В данной работе мы рассмотрели метод анонимизации социальной сети, представленной в виде простого графа. Предложенный метод защищает не только на уровне узлов, но и на уровне связи различных узлов. В работе были описаны проблемы, существующие в современных методах оптимизации, предложен практический алгоритм, реализованный на графическом процессоре, который не увеличивает при этом искажения, нанесенные графу в ходе работы метода. Стоит отметить, что метод позволяет увеличить скорость вычисления не только из-за распараллеливания вычислений, но и из-за более эффективного алгоритма.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-60089.

Библиографическая ссылка