Реализация Федеральных государственных образовательных стандартов высшего образования предполагает модернизацию системы математической подготовки бакалавров. В разделе IV «Характеристика профессиональной деятельности выпускников, освоивших программу бакалавриата» ФГОС ВО по направлениям подготовки 44.03.01 и 44.03.05 «Педагогическое образование» (уровень бакалавриата) определены область, объекты и виды профессиональной деятельности выпускников. Исходя из потребностей рынка труда, научно-исследовательских и материально-технических ресурсов в нашем образовательном учреждении программа бакалавриата ориентирована на педагогический вид деятельности. Решение выпускниками профессиональных задач, таких как осуществление обучения и воспитания в сфере образования, использование технологий, соответствующих возрастным особенностям обучающихся и отражающих специфику предметной области, обеспечение образовательной деятельности с учетом особых образовательных потребностей, формирование образовательной среды для обеспечения качества образования, осуществление профессионального самообразования и личностного роста – обосновывает актуальность использования в вузовском обучении активных и интерактивных форм. И далее: «Удельный вес занятий, проводимых в интерактивных формах, определяется главной целью ООП, особенностью контингента обучающихся и содержанием конкретных дисциплин. В целом в учебном процессе они должны составлять не менее 20 % аудиторных занятий» [4, 5, 6].
В педагогической науке давно применяется термин «активные методы и формы обучения». Он объединяет группу педагогических технологий, достигающих высокого уровня активности учебной деятельности. Активные методы обучения предполагают взаимодействие студентов и преподавателя и направлены на развитие у студентов продуктивного мышления, практических навыков, расширение и углубление знаний, вовлечение обучающихся в процесс решения нестандартных задач [2, 7].
В последнее время в педагогическую науку именно «ворвался» ещё один термин – «интерактивное обучение». В условиях реализации стандартов не просто инновацией, а обязательным требованием стало его распространение и применение в образовательном процессе.
Понятие «интерактивный» происходит от английского «interact» («inter» – «взаимный», «act» – «действовать»). В этой связи под понятием «интерактивные методы» понимают методы, которые позволяют обучающимся взаимодействовать между собой, а под «интерактивным обучением» – «способ познания, осуществляемый в формах совместной деятельности обучающихся» [1, 3].
Интерактивное обучение – это специальная форма организации образовательного процесса, суть которой состоит в совместной деятельности учащихся над освоением учебного материала по решению общих, но значимых для каждого проблем, в обмене знаниями, идеями, способами деятельности. К методам интерактивного обучения относятся те, которые способствуют вовлечению в активный процесс получения и переработки знаний (мини-лекция, работа в группах, контрольный лист или тест, ролевая игра, игровые упражнения, разработка проекта и др.).
В данной статье авторы описали систему математической подготовки студентов-бакалавров по направлению подготовки «Педагогическое образование» (уровень бакалавриата) в Елецком государственном университете имени И.А. Бунина.
В совокупности с другими дисциплинами базовой и вариативной частей ФГОС ВО изучение дисциплины «Математика» направлено на формирование общекультурных, общепрофессиональных и профессиональных компетенций бакалавра педагогического образования.
Современный учитель поставлен перед выбором собственной методики обучения, направленной на всестороннее развитие личности школьника средствами предмета. Учитывая, что в настоящее время в школе используются как традиционные, так и вариативные учебники математики, от учителя требуется не только методическое мастерство, но и глубокое понимание сути математических понятий и фактов. Прежде всего, необходимо знание научных основ курса математики: различных подходов к определению понятия натурального числа, понятия величины и её измерения, понятия функции и функциональной зависимости между величинами, знание алгебры и геометрии.
Высшая школа должна формировать целостную систему универсальных знаний, умений и навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть ключевые компетенции, определяющие качество содержания образования.
В рабочей программе учебной дисциплины «Математика» поставлены конкретные цели и задачи изучения, определено место дисциплины в структуре основной образовательной программы высшего образования, указан перечень планируемых результатов обучения. Содержание дисциплины конкретизировано: выделены основные модули дисциплины, распределение часов курса по темам и видам работ (контактная работа, самостоятельная работа). Раздел «Образовательные технологии» предусматривает планирование активных и интерактивных форм проведения учебных занятий. Особую практическую ценность имеет методический инструментарий, представленный в разделе «Фонд оценочных средств для проведения аттестации обучающихся». В него вошли: перечень форм контроля, матрица формирования компетенций, паспорт фонда оценочных средств по дисциплине «Математика», разнообразные контрольно-измерительные материалы, перечень вопросов к экзаменам и зачетам. Учебно-методическое обеспечение дисциплины предусматривает выполнение требований стандарта. Библиотечный фонд укомплектован печатными и электронными изданиями основной учебной литературы, изданными за последние 10 лет, включает официальные, справочно-библиографические и специализированные периодические издания. В этой связи отметим, что в раздел основной литературы входит учебно-методическое пособие «Математика», разработанное авторами статьи (Елецких И.А. Математика (Часть I, II): Учебник для вузов / И.А. Елецких, Т.М. Сафронова, Н.В. Черноусова – Елец: ЕГУ им. И.А. Бунина, 2014, 2015). Электронно-библиотечная система обеспечивает возможность индивидуального доступа для каждого обучающегося к сети Интернет.
Перечень информационных технологий ориентирует преподавателей и обучающихся на использование в образовательном процессе информационных технологий и информационно-справочных систем. Своеобразным ноу-хау являются довольно емко представленные в программе методические указания и материалы для обучающихся и преподавателей по всем видам учебной деятельности.
Дисциплина «Математика» относится к обязательным дисциплинам вариативной части блока 1. На наш взгляд, процесс изучения дисциплины «Математика» должен быть направлен на формирование следующих компетенций:
а) общекультурных (ОК):
ОК-3: способность использовать естественнонаучные и математические знания для ориентирования в современном информационном пространстве;
ОК-6: способность к самоорганизации и самообразованию
б) профессиональных (ПК):
ПК-1: готовность реализовывать образовательные программы по предмету в соответствии с требованиями образовательных стандартов.
Реализация компетенций ФГОС, обеспечение качества содержания образования явились основанием для создания вышеуказанного учебно-методического пособия для студентов-бакалавров. Структура пособия такова: теоретический материал разбит на 18 тем, темы – на параграфы. Порядок расположения тем не является произвольным, а задан в соответствии с рабочей программой дисциплины. Обратим внимание на отличия пособия от ранее изданных. Они заключаются в учете особенностей преподавания дисциплины в рамках классического университета и вариативности подходов изложения материала в современных учебниках математики для начальной школы. Использование данного пособия в учебном процессе позволит преподавателям осуществлять уровневую дифференциацию, включать студентов в активную учебную деятельность и повышать ее мотивацию, реализовывать интерактивные формы обучения.
Использование интерактивных методов в процессе изучения дисциплины предполагает следующую деятельность преподавателя:
- подготовка темы, вопросов и заданий для обсуждения в группах;
- включение в процесс познания всех студентов группы – организация индивидуальной, парной и групповой работы;
- создание среды образовательного общения (организация взаимодействия всех обучающихся, обмен знаниями, идеями, способами деятельности, накопление совместного знания, возможность взаимной оценки и контроля);
- консультации (помощь в использовании уже имеющегося опыта у студентов, помощь в поиске решения уже поставленных задач и в постановке новых и т.д.);
- контроль выполнения намеченного плана занятия.
Приведем некоторые примеры.
Лекционное занятие по теме «Элементы теории множеств и математической логики» авторы предлагают провести в форме лекции-диалога. Диалог начинается с попытки студентов самостоятельно дать определение понятию «множество». Возникает дискуссия, в ходе которой студенты «открывают» для себя давно известные и сформулированные в науке понятия, определения, законы. Занятие сопровождается использованием презентационного материала.
Практическое занятие по теме «Способы математического доказательства. Правильные и неправильные рассуждения. Простейшие правила вывода» рекомендуется проводить с использованием работы в группах. При рассмотрении способов математических доказательств студенты разбиваются на небольшие группы, каждая из которых получает конкретное задание: подобрать из школьного курса геометрии теоремы, доказательство которых проводится тем или иным (указанным преподавателем) способом.
Важной составляющей образовательного процесса является контроль знаний, умений и навыков обучающихся. Авторы пособия широко применяют в практической деятельности различные виды тестового контроля.
Напомним, что тест для выявления результатов обучения – это совокупность заданий, сориентированных на определение уровня усвоения содержания обучения. Тестовый контроль при изучении математики будущими учителями начальных классов может использоваться на различных этапах обучения. Его можно использовать для проверки усвоения как теоретического, так и практического материала. Естественно, что особую значимость имеет грамотность в составлении тестовых заданий. Только грамотно составленные тесты позволяют определять уровень усвоения знаний и степень формирования навыков в процессе обучения.
Согласно общепризнанным критериям теории и методики преподавания математики правильно составленные тесты должны быть:
- относительно краткосрочными, т.е. не требовать больших затрат времени;
- однозначными, т.е. не допускать произвольного толкования тестового задания;
- правильными, т.е. исключать возможность формулирования многозначных ответов;
- относительно краткими, требующими сжатых ответов;
- информационными, т.е. такими, которые обеспечивают возможность соотнесения количественной оценки за выполнение теста с порядковой или даже интервальной шкалой измерений;
- удобными, т.е. пригодными для быстрой математической обработки результатов;
- стандартными, т.е. пригодными для широкого практического использования.
Следует также отметить, что для оценки качества подготовки студентов на соответствие требованиям государственных образовательных стандартов авторы используют модель, построенную на оценке освоения модулей дисциплины, формирующих вышеуказанные компетенции.
Приведем пример варианта тестового задания по теме «Расширение понятия числа» для будущих бакалавров по направлению подготовки Педагогическое образование (направленность /профиль Начальное образование), который предлагался студентам при проведении промежуточного контроля знаний.
По конструкции тест состоит из трех частей. Первая часть (задания А1–А4) ориентирована на проверку степени усвоения тех понятий, терминов, положений теории, которые изучались на предшествующих этапах обучения. Если информации об этом у преподавателя нет, то он лишен возможности проектирования и управления в учебном процессе, выбора оптимального его варианта.
Вторая часть (задания В1–В4) имеет более традиционный для тестов вид: сформулировано задание и предложены варианты ответов на него. Причем, чтобы выбрать правильный ответ, студент должен выполнить определенный набор операций. Преподаватель может потребовать от студента приложить к выбранным вариантам ответов проделанные расчеты, но можно ограничиться и только выбором ответов.
Третья часть (задания С1–С2) предусматривает представление полного варианта решения.
Время выполнения приведенного теста 90 минут.
В заданиях А1 – А4 вместо точек вставьте пропущенные слова так, чтобы получилось истинное утверждение:
А1. Для того чтобы дроби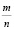 
и 
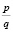были равны ….
А2. Произведением положительных рациональных чисел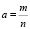 
и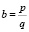 
называется ….
А3. Дробь называется чисто периодической, если ….
А4. Для того чтобы несократимая дробь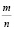 
была равна бесконечной десятичной периодической дроби, необходимо и достаточно, чтобы ….
В заданиях В1 – В4 выберите правильный ответ:
В1. Наименьший общий знаменатель дробей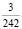 
и 
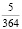равен
1) 44044
2) 1960
3) 588
4) 88088
В2. Число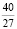 
можно записать следующей десятичной дробью
1) 0,(148)
2) 1,48
3) 1,48(148)
4) 1,(481)
В3. Значение выражения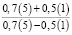 
равно
1) 
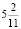
2) 6
3) 
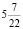
4) 1
В4. Значение выражения в виде несократимой дроби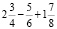 
равно
1) 
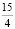
2) 
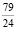
3) 
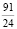
4) 
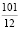
В заданиях С1 – С2 привести полное решение:
С1. Решите задачу арифметическим методом: «В трех гаражах помещается 460 машин. Число машин в первом гараже составляет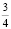 
числа машин, помещающихся во втором, а в третьем гараже в 
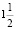раза больше машин, чем в первом. Сколько машин в каждом гараже?»
С2. Доказать, что не существует рационального числа, квадрат которого равнялся бы 7.
Следует отметить, что устный контроль знаний (особенно теоретического материала) способствует выработке быстрой реакции ответов на поставленные вопросы, но письменная проверка позволяет получить более объективные результаты. При письменном контроле студент более сосредоточен, он глубже обдумывает варианты ответа, старается более четко и лаконично сформулировать свою мысль. По нашему мнению, применение тестов при контроле целесообразно и потому, что они задают направление мыслительной деятельности студентов, приучают их варьировать процесс переработки воспринимаемой информации.
В заключение сформулируем основные преимущества активных и интерактивных методов обучения перед пассивными (традиционными) методами и проблемы, возникающие при их использовании.
Реализацию компетентностного подхода, личностно-ориентированное обучение (то есть индивидуальное, учитывающее особенности личности, интересы и потребности каждого студента), возможность для преподавателя емко и сжато представить любой объем учебной информации, улучшение восприятия и упрощение процесса усвоения материала и, наконец, развитие познавательной самостоятельности обучающихся можно отнести к основным преимуществам активных и интерактивных методов обучения. Но даже они не всегда способны преодолеть нежелание студента участвовать в процессе обучения. Для одних студентов активные методы представляются чем-то, что разрушает их привычное представление о процессе обучения, а для других, например, работа в группе является возможностью не участвовать в образовательном процессе. А уж если преподаватель недостаточно владеет методиками применения интерактивных методов, то процесс обучения может превратиться в анархию.
Проблема изучения возможностей и использования активных и интерактивных форм обучения, выявления их преимуществ и недостатков остаётся актуальной.
Библиографическая ссылка
Елецких И.А., Сафронова Т.М., Черноусова Н.В. СИСТЕМА МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ БАКАЛАВРОВ В СВЕТЕ МОДЕРНИЗАЦИИ ВЫСШЕГО ОБРАЗОВАНИЯ // Современные наукоемкие технологии. – 2016. – № 11-1. – С. 105-109;URL: https://top-technologies.ru/ru/article/view?id=36367 (дата обращения: 21.11.2024).