Анализ информативных и метрологических возможностей датчиков информации современных систем активной безопасности транспортных средств показывает, что они не удовлетворяют требованиям обеспечения безопасности движения. Поэтому актуальна разработка таких датчиков, позволяющих создать многофункциональные системы, совмещающие в себе перечень технических характеристик [3] и экономическую целесообразность [2]. Такими качествами обладают системы технического зрения (СТЗ), совмещающие в себе многофункциональность зрения человека и высокие метрологические характеристики технических измерительных систем. Такая измерительная система представляет собой инструмент как для решения задач мониторинга местоположения, так и автоматического управления движением транспортных средств, в различных условиях их применения.
Однако СТЗ, широко используемые в промышленности, для контроля и управления технологическими процессами имеют улучшенные условия применения [5]. Объект контроля, как правило, хорошо освещен и расположен непосредственно перед объективами СТЗ, поэтому вопрос о точности измерений практически не возникал. Применяя СТЗ для обеспечения движения транспортных средств, приходится работать в условиях освещения, меняющегося в широких пределах, значительной скорости и удаленности объектов. Вопрос о погрешностях СТЗ транспортных средств становится чрезвычайно актуальным и требует значительных исследовательских усилий.
СТЗ представляет собой оптико-электронную систему на основе нескольких разнесенных фотокамер, связанных с производительным вычислителем, который обеспечивает обработку изображений с целью нахождения особых точек. Такая система в общем случае «видит» объемно, поскольку декартовы координаты всех особых точек определяются с точностью недоступной для радиолокационных датчиков. Важным улучшением возможностей такой системы является совместное использование как оптического, так и инфракрасного диапазонов спектра. В этом случае система может быть даже эффективней человеческого зрения при плохой видимости вследствие факторов ухудшающих видимость. Система контроля за дорожной (воздушной, водной) ситуацией может быть использована для автоматизации управления транспортными средствами в целях повышения безопасности движения, а также снижения психофизической нагрузки на водителя.
На рисунке представлена СТЗ с двумя разнесенными цифровыми фотокамерами.
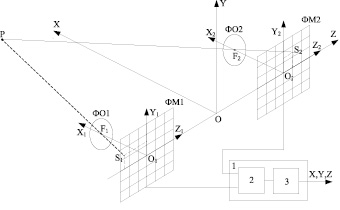
СТЗ с параллельными оптическими осями
Здесь ФМ1, ФМ2 – фоточувствительная матрица первой и второй фотокамеры; ФО1, ФО2 – фотообъектив первой и второй фотокамеры; 1 – вычислитель; 2 – модуль программной обработки изображений; 3 – модуль вычисления координат точки Р (x, y, z).
Цифровой вычислитель (1) обеспечивает программную обработку изображений объекта и вычисление координат объекта по координатам изображений точек S1 и S2 на фотоматрицах первой и второй фотокамер. Программная обработка изображения осуществляется с применением методов использующих оконтуривание изображения и дальнейшее выделение в нем точек излома или срединной точки контура [4].
Для идеальной СТЗ процесс определения координат точечного объекта заключается в расчете по формулам
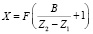 , (1)
, (1)
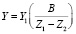 , (2)
, (2)
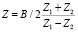 , (3)
, (3)
где Y1 = Y2, Z1, Z2 – координаты изображений точки на первой и второй фотоматрицах; X, Y, Z – координаты точечного объекта в системе OXYZ; F1 = F2 = F – фокусное расстояние объективов фотокамер.
Математическая модель погрешностей СТЗ
Поскольку идеальную систему создать невозможно, возникает вопрос о связи погрешности измерений с технологическим несовершенством СТЗ. Рассмотрим процесс измерения координат объекта посредством двух разнесенных фотокамер, оптические оси которых незначительно отклонены от идеального положения в пространстве, в отличие от СТЗ с параллельными осями [1].
Соотношения, обеспечивающие измерения для СТЗ, имеющей малые линейные и угловые дефекты установки фотокамер, а также некоторое различие в фокусировке их объективов, имеют следующий вид
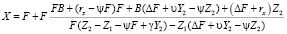 , (4)
, (4)
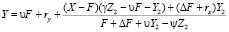 , (5)
, (5)
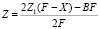 , (6)
, (6)
где 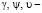 малые углы поворота правой фотокамеры относительно левой вокруг осей X, Y, Z;
малые углы поворота правой фотокамеры относительно левой вокруг осей X, Y, Z; 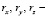 координаты вектора смещения правой камеры от идеального положения с координатами (0, 0, В/2),
координаты вектора смещения правой камеры от идеального положения с координатами (0, 0, В/2), 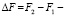 отклонение фокусного расстояния правой фотокамеры от фокусного расстояния левой.
отклонение фокусного расстояния правой фотокамеры от фокусного расстояния левой.
Выражения для определения координат точечного объекта являются функциями координат изображений точки на фотоматрицах Y1, Z1, и Y2, Z2, а также величин, 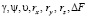 . Разложим в ряд Маклорена [1] по переменным
. Разложим в ряд Маклорена [1] по переменным 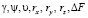 , причем учтем члены не выше первого порядка малости.
, причем учтем члены не выше первого порядка малости.
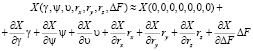 , (7)
, (7)
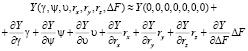 , (8)
, (8)
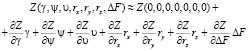 . (9)
. (9)
Перепишем соотношения (7), (8), (9) в более компактной матричной форме
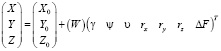 , (10)
, (10)
где 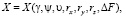
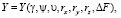
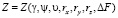 – измеряемые координаты точечного объекта; начальные значения координат для СТЗ без дефектов
– измеряемые координаты точечного объекта; начальные значения координат для СТЗ без дефектов 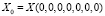 ,
, 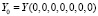 ,
, 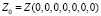 ;
;
 . (11)
. (11)
С учетом выражений, полученных для производных, запишем искомые разложения в ряд.
Первые слагаемые представляют собой координаты X0, Y0, Z0, измеренные идеальной СТЗ. Остальные слагаемые описывают влияние соответствующих дефектов на результат измерения координаты.
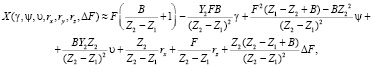 (12)
(12)
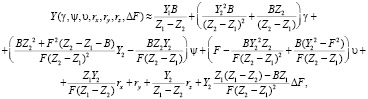 (13)
(13)
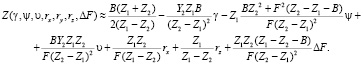 (14)
(14)
Выражения (12), (13), (14) могут быть использованы как для алгоритмической компенсации ошибок измерения, так и для исследования влияния дефектов изготовления СТЗ на ее точностные характеристики.
Погрешности СТЗ, обусловленные асинхронной фотоэкспозицией фотокамер
Пусть выполняется асинхронное фотоэкспонирование точечного объекта, а время между экспозициями левой и правой фотокамер обозначим t. При пространственном перемещении СТЗ за промежуток времени правая камера совершит следующее перемещение
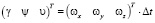 , (15)
, (15)
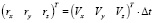 . (16)
. (16)
Тогда к моменту фотоэкспозиции правой камеры вектор, характеризующий несовершенства СТЗ, будет равен
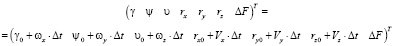 , (17)
, (17)
а вектор измеренных координат будет равен
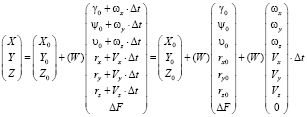 , (18)
, (18)
где второе слагаемое обусловлено статическим несовершенством установки правой камеры относительно левой, а третье слагаемое обусловлено асинхронизмом фотоэкспозиции фотокамер и проявляется при угловом и линейном движении СТЗ.
Погрешности СТЗ, обусловленные дискретностью фотоматрицы
Для получения соотношений, описывающих эти погрешности, воспользуемся выражениями координат без учета несовершенства установки фотокамеры, то есть rx = ry = rz = ψ = γ = υ = D = 0.
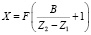 ,
, 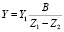 ,
, 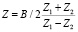 . (19)
. (19)
Получим выражения для полного дифференциала координат X, Y, Z
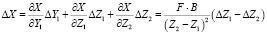 , (20)
, (20)
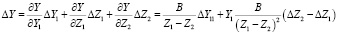 , (21)
, (21)
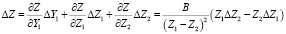 . (22)
. (22)
Вычислим предел абсолютной допускаемой погрешности измерения координат X, Y, Z.
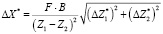 , (23)
, (23)
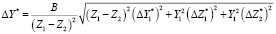 , (24)
, (24)
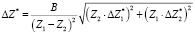 , (25)
, (25)
где пределы абсолютных допускаемых погрешностей измерения координат 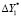 ,
, 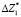 ,
, 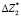 .
.
Погрешности дискретизации измерения координат точечного объекта растут по квадратичному закону с увеличением дальности.
Погрешности СТЗ, обусловленные шумами фотоматриц
Оценка таких погрешностей должна производиться с учетом технологии обработки изображения. Рассмотрим подход к обработке изображений, основанный на нахождении центра «тяжести» области изображения.
Центр яркости изображения особой точки
Найдем границу изображения особой точки, причем в качестве порогового значения выберем величину близкую к половине наибольшего значения яркости Rпор = 130 (≈ 255/2). Пусть средняя часть изображения маяка удовлетворяет условию Rij ≥ Rпор (где i и j – номера пикселов в строке и столбце соответственно для области K).
Координаты центра яркости изображения особой точки вычислим по формулам
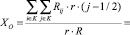
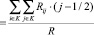 , (26)
, (26)
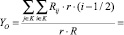
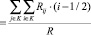 , (27)
, (27)
где r – размер пиксела, Rij – яркость красного пиксела в зависимости от номера строки (i) и столбца (j), К – область изображения, удовлетворяющая условию Rij ≥ Rпор, 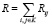 – мощность излучения области K.
– мощность излучения области K.
Оценка математического ожидания случайной величины вычисляется по формуле
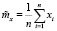 , (28)
, (28)
где n – объем выборки случайной величины.
Так как величина представляет собой сумму n независимых одинаково распределенных случайных величин ξi, а выборка измерений – совокупность реализаций этих случайных величин, то согласно центральной предельной теореме при достаточно большом n ее закон распределения близок к нормальному с математическим ожиданием mx и среднеквадратическим отклонением σх.
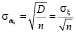 , (29)
, (29)
где σξ – среднеквадратическое отклонение генеральной совокупности.
Последнее соотношение показывает, что «групповая» обработка изображения, основанная на суммировании (26), (27), уменьшает влияние шумов фотоматрицы на результат определения координат особой точки.
Таким образом, СТЗ является хорошим измерительным средством на малой дистанции от измеряемого объекта.
Погрешности измерений, обусловленные дискретизацией изображения, растут пропорционально квадрату расстояния, поэтому для измерений на больших дистанциях необходима субпиксельная обработка изображений. Аналогичный положительный эффект дает «групповая» обработка изображения, основанная на определении центра яркости окрестности особой точки.
Математическая модель погрешностей СТЗ, обусловленных технологическим несовершенством установки фотокамер, позволяет не только оценивать погрешности на этапе конструирования СТЗ, но и реализовать алгоритмическую компенсацию ошибок.
Библиографическая ссылка
Кудаев А.Н., Бондарев В.Г., Бобров В.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОГРЕШНОСТЕЙ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ // Современные наукоемкие технологии. 2016. № 11-1. С. 45-50;URL: https://top-technologies.ru/ru/article/view?id=36355 (дата обращения: 13.02.2026).



