Настроечные параметры пропорционально-интегрально-дифференциального (ПИД) регулятора являются результатом синтеза аналогового регулятора [3, 8]. Но переход к цифровому регулированию с полученными значениями настроечных параметров сопровождается негативными последствиями регулирования: полученные значения параметров не гарантируют требуемую динамику. Необходима корректировка параметров регулятора по факту реализации в конкретной цифровой схеме, что подчас соизмеримо со сложностями начального синтеза регулятора.
С другой стороны, известны упрощённые методики настройки ПИД-регуляторов, например Ziegler–Nichols (1942) [10], Chien–Hrones–Reswick (1952) [6], Cohen–Coon (1953) [7], Wang–Juang–Chan (1995) [9], несравнимые по своей сложности с полноценным процессом синтеза регулятора и уже только поэтому крайне полезные в практическом плане. Но и они при переносе значений настроечных параметров на организуемые процессы прямого цифрового регулирования (Direct Digital Control – DDC) требуют непростой корректировки для обеспечения подходящей динамики регулируемого параметра.
Поэтому потребность решения вопросов настройки цифровых регуляторов, то есть в реальности вопросов формирования подходящей дискретной модели ПИД-регулятора, не ослабевает и до настоящего времени является актуальной.
В работе предлагается система моделирования процессов цифрового регулирования и программные инструментальные средства для использования методики Зиглера – Николса (Ziegler-Nichols) для определения параметров цифрового ПИД-регулятора и улучшения динамики регулируемого параметра.
Оценка рынка средств настройки регуляторов
Анализ программных продуктов последнего пятилетия, зарегистрированных в ФГБУ «Федеральный институт промышленной собственности» [5], показал наличие около полусотни программ настройки регуляторов, среди которых по эффективности, по-видимому, можно выделить следующие: «Нейросетевая надстройка над ПИД-регулятором для адаптации его параметров (Нейросетевой оптимизатор)» (Ю.И. Ерёменко, Д.А. Полещенко, А.И. Глущенко; ФГАОУ ВПО «МИСиС»; Свидетельство о гос. регистрации № 2013614835, 2013), позволяющая подобрать подходящие настроечные параметры ПИД-регулятора на основе пятнадцати параметров о ситуации на объекте регулирования с помощью нейронной сети и базы продукционных правил, существенным ограничением которой являются субъективные экспертные знания, обуславливающие весь процесс вывода; «Программа расчета коэффициентов пропорционально-интегрально-дифференциального регулятора с нечеткой адаптацией с четкими терм-множествами» (А.В. Богданов; ФГБОУ ВПО ОГУ; Свидетельство о гос. регистрации № 2016612060, 2016), настраивающая ПИД-регулятор с нечеткой адаптацией и строящая структуру системы продукционных правил нечеткого регулятора с адаптацией коэффициентов ПИД-регуляторов, использующих четкие терм-множества. Существенным ограничением используемой методики, реализованной в программе, по нашему мнению, также является ориентация на специфические экспертные процедуры; «Исследование свойств пропорционально-интегрально-дифференциального регулятора» (А.А. Павленко; ФГБОУ ВПО «АлтГТУ им. И.И. Ползунова»; Свидетельство о гос. регистрации № 2015617749, 2015), позволяющая рассчитать оптимальные параметры аналогового регулятора по методу Зиглера –Николса и получить динамическую модель поведения объекта управления, что не совсем приемлемо для использования в структурах прямого цифрового управления; «Система регистрации и отображения параметров состояния и формирования команд управления и регулирования объектом» (ООО «Компания СК-Инжиниринг», Свидетельство о гос. регистрации № 2013619409, 2013), направленная на настройку аналоговых ПИД-регуляторов для обеспечения необходимого качества регулирования, что также недостаточно подходит для использования в DDC; «Параметрическая оптимизация системы с ПИД-регулятором по различным критериям качества при помощи генетического алгоритма» (Н.Н. Куцый, Н.Д. Лукьянов; ФГБОУ ВПО ИрГТУ; Свидетельство о гос. регистрации № 2014611433, 2014). Программа реализует параметрическую оптимизации на базе генетического алгоритма за счет предварительного задания границ изменения настраиваемых параметров, критериев качества и параметров генетического алгоритма. Результаты работы программы представлены в текстовом и графическом виде. Существенным ограничением используемой методики, реализованной в программе, по-видимому, является ориентация на настройку аналоговых регуляторов; «Исследование процесса настройки параметров типовых регуляторов с использованием непараметрической модели» (А.В. Банникова, Н.А. Сергеева; ФГАОУ ВПО СФУ; Свидетельство о гос. регистрации № 2014616687, 2014). В программе можно задавать закон регулирования (пропорциональный, пропорционально-интегральный, ПИД), параметры управления, тип задающего воздействия и просматривать результаты моделирования в графической форме для аналоговых регуляторов; «Гибридный нейросетевой ПИД-регулятор системы управления квадрокоптера» (А.А. Евгенов; ФГБОУ ВПО ЮРГПУ (НПИ); Свидетельство о гос. регистрации № 2013661953, 2013). Программное средство позволяет вычислять оптимальные параметры ПИД-регулятора квадрокоптера без привязки к особенностям цифрового ПИД-регулятора; «Digital control system with PID Controller (DPC)» (В.П. Кривошеев, Б.А. Кан; ФГБОУ ВПО ВГУЭС; Свидетельство о гос. регистрации № 2014611772, 2014). Программная система позволяет рассчитать настроечные параметры цифровой одноконтурной системы управления с аналоговым ПИД-регулятором методом Гаусса – Зейделя; «Программный комплекс для автоматизации испытаний синхронных неявнополюсных электрических машин (SMTest.exe)» (Д.А. Исцелемов, Э.В. Любимов; ФГБОУ ВПО ПНИПУ; Свидетельство о гос. регистрации № 2015660820, 2015), позволяющий осуществить поиск оптимальных параметров аналогового ПИД-регулятора с обратной связью по току возбуждения машины; «Программа имитационного моделирования управления центром тяжести крестокрылого снаряда в боковом движении» (О.В. Куприянова, Б.Н. Лелянов; ФГБОУ ВПО ТОГУ; Свидетельство о гос. регистрации № 2015615032, 2015). Программная система позволяет задавать постоянные коэффициенты аналогового ПИД-регулятора и просматривать результаты моделирования системы управления.
Таким образом, оценивая рынок средств настройки регуляторов, можно говорить о том, что в последних отмеченных достижениях программных продуктов, как и ранее, не учитывают два основных качества функционирования цифрового ПИД-регулятора: во-первых, то, что управляющее воздействие вычисляется и формируется в процессоре регулирования по дискретным вариантам континуальной модели регулятора, для каждого варианта из которых могут быть эффективными (подходящими) разные наборы настроечных параметров и, во-вторых, что все параметры дискретных моделей, включая и время дискретизации (время опроса датчиков, задержки реакции объекта регулирования и пр.), участвуют в формировании особенностей динамики регулируемых параметров.
Программный инструментарий интерактивного поиска настроечных параметров цифрового регулятора
Предлагаемая структура программного инструментария обусловлена двумя системными положениями: 1) процесс цифрового регулирования – это единство моделей регулятора и объекта регулирования и 2) каждый компонент цепи регулирования влияет на качество регулируемого параметра. Поэтому в предлагаемой структуре программного инструментария (рис. 1) реализовано: задание моделей цифрового ПИД-регулятора с различным представлением интеграла в континуальной модели (по формулам прямоугольника, трапеции и Симпсона [4]):
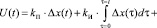
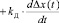, (1)
где U(t) – управляющее воздействие в момент времени t; kП, kИ и kД – настроечные параметры; Δx(t) – рассогласование в момент t (t = n·T, n = 0, 1, 2, …; T – время опроса); задание модели объекта регулирования (ОУ) в виде токового контура двигателя постоянного тока:
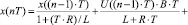
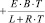, (2)
где R – сопротивление обмотки якоря; L – индуктивность цепи якоря; B – коэффициент передачи датчика тока; E – ЭДС самоиндукции; интерактивный поиск для пропорционального регулятора коэффициента передачи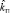 
, при котором система находится на границе устойчивости, и периода установившихся в системе колебаний 
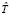для расчета настроечных параметров методом Зиглера – Николса; вычисление настроечных параметров по Зиглеру – Николсу [10]:
, 
, 
;
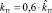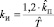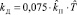одновременное отображение динамики регулируемого параметра выбранных моделей автоматического регулирования с цифровым регулятором для выбора модели с требуемой динамикой регулируемого параметра; ведение истории экспериментов для сохранения моделей цифрового регулирования; изменение и выбор моделей для отображения динамики регулирования; варьирование с шагом настроечными параметрами (kП, kИ, kД) цифрового регулятора.
Интерактивный программный поиск настроечных параметров
Структура предложенного программного инструментария апробирована [1, 2] и показала возможности интерактивного подбора коэффициента передачи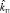 
и дискреты 
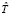для пропорционального регулятора и вычисления настроечных параметров по методике Зиглера – Николса (рис. 2).
Моделирование системы регулирования, например, по формуле прямоугольника с полученными данными (рис. 2) показало неустойчивую динамику регулирования (рис. 3 А), которую можно подкорректировать предложенным инструментарием варьирования настроечных параметров (рис. 3 Б), а использование моделей цифрового ПИД-регулятора по методам трапеции и Симпсона в большинстве случаев дает положительные результаты (рис. 3 B).
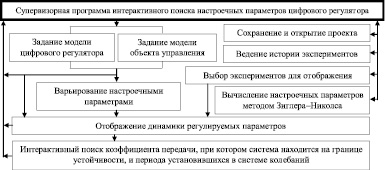
Рис. 1. Структура программного инструментария интерактивного поиска настроечных параметров цифрового ПИД-регулятора
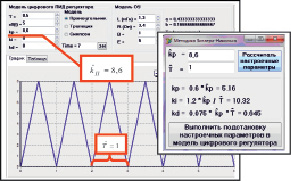
Рис. 2. Интерактивное определение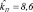 
, 
(для пропорционального регулятора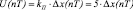 
и модели (2) с параметрами L = 1,3; R = 3,4; B = 1; E = 5) и вычисление настроечных параметров по методике Зиглера – Николса
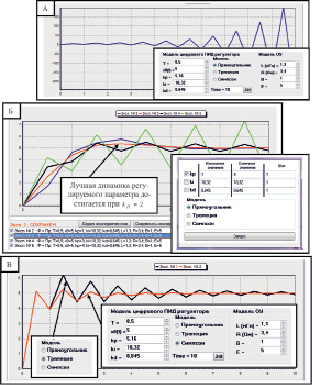
Рис. 3. Пример моделирования динамики регулируемого параметра, где: А) применена цифровая модель регулятора по формуле прямоугольника; Б) варьирование настроечного параметра kП для корректировки модели рис. 3, А; B) применены цифровые модели регулятора по формулам трапеции и Симпсона
Выводы
Предложена структура программных инструментальных средств интерактивного поиска настроечных параметров цифрового ПИД-регулятора, основанная на системном представлении контура регулирования, отличающаяся применением методики Зиглера – Николса для различных дискретных моделей цифрового регулятора по формулам прямоугольника, трапеции и Симпсона.
Исследование выполнено при поддержке «ОГУ имени И.С. Тургенева» по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ № 7-н/26 от 23.10.2013 г.
Библиографическая ссылка
Захарова О.В., Раков В.И. ИНТЕРАКТИВНЫЙ ПРОГРАММНЫЙ ИНСТРУМЕНТАРИЙ ПОИСКА НАСТРОЕЧНЫХ ПАРАМЕТРОВ ЦИФРОВОГО ПИД-РЕГУЛЯТОРА // Современные наукоемкие технологии. – 2016. – № 11-1. – С. 31-35;URL: https://top-technologies.ru/ru/article/view?id=36352 (дата обращения: 18.04.2024).