Математика как наука и методика ее преподавания существуют уже не одну тысячу лет. Информатика как наука и методика ее преподавания существуют только несколько десятков лет. Изначально именно математика была теоретической основой информатики, но затем несколько десятилетий относительно независимого друг от друга существования этих наук породило, на наш взгляд [1, 2, 3], не только новые достижения, но и новые проблемы.
Почему ошибки программирования специализированных математических пакетов прикладных программ (ППП) с большим трудом устраняются десятилетиями в процессе их эксплуатации? Потому, что математик и программист с трудом понимают друг друга. Множества профессиональных терминов того и другого имеют незначительную область пересечения. Хорошо бы при обучении тех и других эту область расширить. Чем объяснить [3, 8] большую популярность статистического ППП SPSS и малую – аналогичного ППП Statistica? Первый был реализован на компьютерах еще в середине XX века и к настоящему времени имеет более двадцати версий, а второй появился лишь в 1984 году. Заметим, что сейчас правообладателем их обоих является IBM, которая выпустила пакет SPSS-Statistica.
В настоящее время в высших учебных заведениях преподаватели математики и информатики в редких случаях могут заменить друг друга. Причины – различное содержание обучения (причем различное даже на уровне парадигм) и различная методика обучения. Простой пример. С точки зрения математика, теорема с ошибкой существовать и использоваться не может, это и не теорема. А программные средства, содержащие ошибки, существуют и используются. Можно ли информатику отнести к точным наукам?
Тестирование программ и выявление в них ошибок – предмет изучения специальной дисциплины [6] в составе информатики. Существуют особые специалисты – программисты-тестеры. Информатика как наука обеспечивает их инструментами, но эти инструменты сами по себе не могут гарантировать выявления ошибки. Выявление ошибок – это искусство!
Термин «следовательно» имеет в математической логике одно значение, а, например, в политологии – несколько иное, но студент от этого защищен. Он знает, что парадигмы этих наук различны. Математика – точная наука, политология – гуманитарная. Но не столь широко декларируется, что парадигмы [3, 5] математики и информатики тоже различны.
Таким образом, при изучении математики и информатики иногда необходимо обращение к другим научным дисциплинам, необходим междисциплинарный подход.
В настоящее время термин «алгоритм», лежащий в основе информатики, и тот же термин из математической теории алгоритмов – это различные термины. Машина Тьюринга имеет мало общего с моделью компьютера фон-Неймана. А современные компьютеры уже вышли за рамки модели фон-Неймана, поскольку выполняют «параллельные алгоритмы». Современная «формалистская» математика, основу которой заложили труды Гильберта [4], признает только формальные аксиоматические теории (ФАТ), которые мало общего имеют и с аксиоматикой Евклида. Каждая аксиома Евклида имеет смысл в окружающем нас мире и должна быть ему адекватной. Аксиомы по Гильберту – это просто последовательности символов из некоторого алфавита, они преобразуются по формальным правилам в другие последовательности символов, какого-либо смысла в окружающем нас мире у них быть не должно, как и адекватности. По Гильберту истинности и ложности «вообще» не существует, они имеют смысл только в рамках конкретной ФАТ.
Машина Тьюринга является ФАТ. Если «алгоритм» – это машина Тьюринга, то и он – это тоже ФАТ. Модель фон-Неймана – это обобщенная модель некоторой технической конструкции, она ФАТ не является, как и «алгоритм», лежащий в основе информатики. «Интуиционистская» математика [1, 7], основу которой заложили Вейль и Брауэр, с легкостью могла бы включить в себя и модель фон-Неймана, и соответствующий «алгоритм». Однако в настоящее время более популярна именно «формалистская» математика.
Таким образом, при изучении математики и информатики иногда необходимо обращение к основаниям математики и к философии науки.
Термин «алгоритм» появился в IX веке [1, 3]. Его источниками явились два трактата великого математика древности Мухаммада ибн Муса аль-Хорезми: «Книга об индийской арифметике» и «Книга о восстановлении и противопоставлении». В первой книге обосновывались преимущества индийской позиционной десятичной системы счисления по сравнению с буквенными греческой и римской системами, а также необходимость нуля для обозначения пустого разряда при записи числа в десятичной системе счисления. Вторая книга содержит описание способов решения алгебраических уравнений первой и второй степени. Термин «алгоритм» использовался для обозначения правил выполнения алгебраических действий (включая извлечение квадратного корня) над числами, записанными в десятичной системе и правил решения алгебраических уравнений первой и второй степени. Таким образом, в IX веке под алгоритмом понимали последовательность некоторых операций, что соответствует современному понятию алгоритма, лежащему в основе информатики. Под операциями понимаются элементарные команды, которые способно выполнять некоторое устройство, в частности, компьютер модели фон-Неймана. Но, например, алгоритм решения квадратного уравнения в действительных числах не является алгоритмом в смысле Тьюринга!
В середине XVII века Паскаль создал механический компьютер. До середины XIX века таблицы, необходимые для артиллерийской стрельбы и других практических применений, рассчитывались с помощью «живых» компьютеров. Такой «компьютер» состоял из 20–30 человек, каждый из которых либо выполнял некоторую элементарную операцию, входящую в состав алгоритма, либо управлял этими людьми, то есть – выполнением алгоритма. Почти все создатели первых электрических компьютеров (например, Д. Атанасофф, Д. Стибиц, К. Цузе, Г. Айкен, Д. Эккерт, Д. Мочли) считали себя математиками. Представление о новой науке, связанной с автоматической обработкой информации [1, 3], появилось лишь во второй половине XX века. В Англии и США ее назвали Computer Science, во Франции и СССР (России) – информатикой.
Если говорить о программировании высокого уровня, то, кроме императивной (процедурной) парадигмы (где программа – это последовательность команд, то есть алгоритм), существуют также неалгоритмические парадигмы (где программа алгоритмом не является). Таковы [6] логическая, функциональная парадигмы, программирование в ограничениях и другие. Программа в логической парадигме – это описание:
1) фактов (их можно считать аксиомами);
2) логических правил вывода;
3) цели (это высказывание, истинность которого нужно проверить).
Программа перебором всех вариантов пытается построить логический вывод цели из имеющихся фактов. Если это удается, то сообщается, что цель истинна. В противном случае – что недостаточно фактов для признания цели истинной. О логическом программировании полезно рассказывать при изучении математической логики и оснований математики. Интерес представляет отсутствие в нем категории ложности цели. Наибольший интерес к таким экстравагантным парадигмам приходился на 60–70-е годы XX века. К 90-м годам XX века предполагался переход на компьютеры с логической архитектурой (компьютеры V поколения) – так называемый «Японский проект». Там даже низкоуровневое программирование предполагалось вести на основе логической парадигмы. В настоящее время интерес к этим экзотическим парадигмам минимален. «Японский проект» кончился ничем. Причина в том, что перебор всех вариантов был «не по зубам» компьютерам конца XX века.
Современное программирование почти всегда императивное. Даже экспертные системы и нейронные сети реализуются с помощью императивных языков [6], например, C++, C#, Java. Объектно ориентированное программирование, как правило, также императивное. В принципе, оно могло бы быть реализовано и не алгоритмически. Объект – это более сложная структура, чем просто число или строка символов. Интересно, что Microsoft в 2010 году разработало язык Visual F#, сочетающий в себе визуальное объектно ориентированное программирование с логической и функциональной парадигмами.
Таким образом, при изучении математики и информатики иногда необходимо обращение к истории развития математики, техники, информатики.
Значительная часть формул, приводимых студентам при изучении математики и информатики, практически не доводится до получения конечного числового результата. Но именно такова цель лабораторных работ, например, по теории вероятностей и математической статистике. Современная вычислительная математика достигает этой цели с помощью компьютера. Поэтому иногда ее относят к информатике. Математическая теория кодирования является фундаментальной основой информатики, и при ее изучении полезно использовать примеры реального кодирования информации.
Международный стандарт IEEE-754 предлагает двоичные форматы действительных чисел. Архитектура современных компьютеров от мэнфреймов до планшетов и смартфонов строится на его основе. Рассказ о нем может быть полезен при изучении программирования, вычислительной математики, теории кодирования, теории вероятностей, математической статистики и других дисциплин.
Согласно IEEE-754 битовое поле действительного числа (табл. 1) длиной w битов состоит из трех полей (S – знака числа, E – двоичного порядка, M – мантиссы) длиной соответственно 1 бит, b битов, n битов. Представленное таким образом действительное число F вычисляется по формуле (1). Отсюда следует, что S = 0 означает знак числа плюс, а S = 1 – минус. E и M – беззнаковые целые двоичные числа. E хранит смещенный на D двоичный порядок, в результате E не может быть отрицательным. Истинный порядок равен E-D. M хранит только дробную часть нормализованной до разряда единиц двоичной мантиссы, разряд единиц является скрытым.
Таблица 1
Битовое поле действительного числа
|
Поле S: 1 бит |
Поле E: b битов |
Поле M: n битов |
|
Всего w битов: w = n + b + 1 |
||
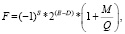 (1)
(1)
где 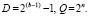
Формула (1) не применяется в следующих 4 исключительных случаях:
1) если S = 0, E = 0, M = 0, то F – это положительный ноль, если S = 1, E = 0, M = 0, то F – это отрицательный ноль;
2) если S = 0, E = 1...1 (заполнена единицами), M = 0, то F – это положительная бесконечность, если S = 1, E = 1...1, M = 0, то F – это отрицательная бесконечность;
3) если E = 1...1, M ≠ 0, тогда F имеет значение NAN (не число, Not A Number);
4) если E = 0, M ≠ 0, то F – это число с денормализованной мантиссой, которое вычисляется по формуле (2).
Стандарт IEEE-754 (табл. 2) предусматривает два обязательных формата действительного числа (Single – число с одинарной точностью, Double – число с двойной точностью) и два не обязательных расширенных формата (Single-extended, Double-extended).
Таблица 2
Форматы действительных чисел
|
Форматы |
w |
b |
n |
|
Single |
32 |
8 |
23 |
|
Single-extended |
≥ 43 |
≥ 8 |
≥ 23 |
|
Double |
64 |
11 |
52 |
|
Double-extended |
≥ 79 |
≥ 11 |
≥ 52 |
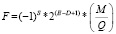 . (2)
. (2)
При изучении данного учебного материала студентам можно дать задание на вычисление по формулам (1) и (2) наименьших и наибольших по абсолютной величине чисел. Студент убеждается в том, что компьютер способен иметь дело только с конечным множеством чисел. Положительные и отрицательные бесконечности и нули (бесконечно малые) вводятся как некоторые значения (это концепция Лейбница XVII–XVIII веков), а не как процессы – последовательности с пределами (это победившая в математике концепция Ньютона). Здесь при обучении студентов следует обратиться к истории математики и рассказать об обеих концепциях и возникновении теории пределов.
Стандарт IEEE-754 требует реализации типов данных Single и Double при фиксированных w, b, n на любом компьютере, чего нельзя сказать про Single-extended и Double-extended. Следовательно, при машинно-независимом программировании для действительных чисел самым широким диапазоном представления чисел обладает тип данных Double. Если при программировании на C, C++, C# мы запишем double X; тогда будет иметь место неравенство 10310 > X > 10-330, это следует из формул (1) и (2). Если наша программа будет вычислять n! при некотором n и результат будет записывать в ячейку X, то, например, при n = 100 в ячейке X верного результата не будет, какой бы не был алгоритм этого вычисления.
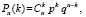 (3)
(3)
где 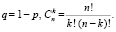
Формула (3) – это формула Бернулли из курса теории вероятностей, Pn(k) – вероятность получить ровно k успехов в n испытаниях Бернулли, p – вероятность успеха в испытании. Почему на практике при больших n эта формула не работает? Почему в этих случаях нужны теоретически более сложные локальная и интегральная формулы Лапласа? Которые, заметим, являются приближенными, а формула Бернулли – точная. Как объяснить это студенту? Потому, что при больших n вычисление n! невозможно при программировании на компьютере с использованием стандартных типов данных. Если методами объектно ориентированного программирования построить нестандартные типы данных для действительных чисел с еще более широким диапазоном представления чисел, тогда будет возможно вычисление n! при еще больших n, но и в этом случае какое-то ограничение на n все равно будет.
Таким образом, при изучении математики и информатики иногда необходимо более подробное рассмотрение ограничений технического характера. В противном случае невозможно полное понимание студентами изучаемого материала. То же самое относится и к другим упомянутым выше методам обучения. А что такое «неполное понимание»? С точки зрения парадигмы математики – это просто непонимание. С более широкой точки зрения, это, по-видимому, восприятие части учебного материала на основе не только логики, но и других принципов, возможно, некоторых эвристических принципов, интуиции.
В заключение заметим, что, помимо математика и информатика, в нашей статье необходимо рассмотреть еще одного фигуранта – педагога. Существует, например, химическая индустрия, и с ней связаны миллионы людей, и существует химия как наука. Химическая индустрия и химия как наука – это не одно и то же, но обществу необходимы и то и другое. Аналогично, существуют образовательная индустрия и педагогика как наука. Аналогично, это не одно и то же, но обществу необходимы и то и другое. Педагогика как наука [1, 3, 8] не может обойтись без эксперимента и статистической обработки его результатов с применением современных информационных технологий (ИТ). Но математик-статистик, специалист в области ИТ и ученый-педагог имеют различные сферы компетенции, если только последний не имел опыта преподавания математической статистики и ИТ. В этом смысле преподаватели математики и информатики имеют значительное преимущество.
Библиографическая ссылка
Фокин Р.Р., Атоян А.А., Абиссова М.А. МЕТОДЫ ОБУЧЕНИЯ В ВЫСШЕЙ ШКОЛЕ, ОБУСЛОВЛЕННЫЕ НЕКОТОРЫМИ КОНЦЕПТУАЛЬНЫМИ И ТЕХНИЧЕСКИМИ ОГРАНИЧЕНИЯМИ ПРИ КОМПЬЮТЕРНОЙ РЕАЛИЗАЦИИ МАТЕМАТИЧЕСКИХ И ИНФОРМАЦИОННЫХ МОДЕЛЕЙ // Современные наукоемкие технологии. 2016. № 10-2. С. 397-401;URL: https://top-technologies.ru/ru/article/view?id=36343 (дата обращения: 07.02.2026).
DOI: https://doi.org/10.17513/snt.36343



