Изучение теории вероятностей в курсе математики высшей школы на технических и экономических направлениях подготовки включает знакомство студентов с законом больших чисел (ЗБЧ). Термин ЗБЧ впервые появился в работах С. Пуассона в 1837 г. [2]. В настоящее время под ЗБЧ «естественно понимать всю совокупность предложений, утверждающих с вероятностью, сколь угодно близкой к единице, что наступит некоторое событие, зависящее от неограниченно увеличивающего числа случайных событий, каждое из которых оказывает на него лишь незначительное влияние» [1, с. 175]. В литературе, предназначенной для организации учебной деятельности студентов вуза, ЗБЧ представлен тремя теоремами (Бернулли, Чебышева, Пуассона) и двумя неравенствами (Маркова и Чебышева) [4, 9].
Изложению теорем Бернулли, Чебышева и Пуассона предшествует знакомство с неравенствами Маркова и Чебышева, понимание закономерностей которых позволяет не только успешно осваивать содержание теорем ЗБЧ, но и более эффективно познавать существенные взаимосвязи вероятностных процессов и явлений. Формирование понятий о соотношениях, отраженных в неравенствах Маркова и Чебышева, начинается с их определения, затем приводится аналитическое доказательство и предлагается для решения система типовых учебных заданий [4, 9]. Такое дидактическое сопровождение с обилием абстрактной символики и отдаленными от реальной действительности задачами не всегда приводит к успешному освоению содержания этих понятий студентами, планирующими получение профессионального образования, ориентированного на прикладное применение математических знаний и умений. В этом случае одним из вариантов достижения желаемых педагогических результатов выступает погружение студентов в выполнение лабораторных заданий.
Современный интернет и программное обеспечение персональных компьютеров, предоставляя огромные возможности в получении и преобразовании числовой и текстовой информации, выступают для преподавателя хорошей технологической основой построения разнообразных видов и форм учебных заданий. Применение имитационного моделирования и вычислительного эксперимента для создания благоприятных условий восприятия вероятностных соотношений при изучении ЗБЧ, предложено в публикациях [5, 6], а использование статистических данных при проведении лабораторного исследования представлено в данной работе.
Результаты исследования и их обсуждение
Построение математических суждений и умозаключений с опорой на моделирование существенных взаимосвязей всегда создают благоприятные условия для познания студентами окружающей действительности, а обобщение результатов учебного исследования выступает основой развития продуктивной мыслительной деятельности.
Идея освоения вероятностных закономерностей. Изучение неравенств Маркова и Чебышева в вузовском курсе математики, проводимое по схеме от определения к доказательству и решению типовых задач, дополняется лабораторно-практическим заданием по иллюстрации вероятностных закономерностей с привлечением статистических данных. Такой подход основывается на взаимосвязи классического и статистического определений вероятности события. Информацию о значениях различных социальных, экономических, технологических, экологических и других показателей можно найти на сайте Федеральной службы государственной статистики (www.gks.ru).
Реализация методической идеи имеет три составляющие:
1) методическая разработка выполнения лабораторно-практического задания;
2) организация исследовательской деятельности студентов на учебных занятиях;
3) анализ продуктивности мыслительной деятельности субъектов образовательного процесса.
Предлагаемое лабораторно-практическое задание «Проверка адекватности математических моделей неравенств ЗБЧ» включает две части: иллюстрация вероятностных закономерностей неравенства Маркова и иллюстрация вероятностных закономерностей неравенства Чебышева. Прохождение каждой части лабораторно-практического задания распределяется на четыре этапа:
1) определение функциональных зависимостей;
2) составление наглядной модели дискретной случайной величины;
3) построение графических моделей функциональных зависимостей;
4) интерпретация полученных результатов.
Иллюстрация вероятностных закономерностей неравенства Маркова. Неравенство Маркова утверждает, что для любого положительного числа а, вероятность P(X ≥a) того, что неотрицательная случайная величина Х превысит или будет равна а, ограничена сверху величиной, равной отношению её математического ожидания MX к числу a.
Первый этап. Запись неравенства Маркова имеет вид [4, 9]
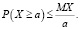 (1)
(1)
Математическое ожидание MX вычисляется по формуле [4, 9]
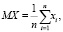 (2)
(2)
где xi – i-е значение дискретной случайной величины Х; n – количество значений дискретной случайной величины Х.
Если положительное число а в неравенстве (1) рассматривать как независимую переменную, то можно ввести две функциональные зависимости f1(a) = P(X ≥ a) и f2(a) = MX / a.
Второй этап. Наглядной моделью дискретной случайной величины Х может служить совокупность статистических данных о каком-либо показателе. Например, выберем Х как выбросы загрязняющих атмосферу веществ, отходящих от стационарных источников, за первое полугодие 2015 г. в различных субъектах Российской Федерации [3] (упорядоченные по возрастанию значения Х представлены в табл. 1).
Количество значений n случайной величины Х равно 83, минимальное и максимальное значения равны соответственно 0,23 и 689,68. Математическое ожидание MX, вычисленное по формуле (2), равно 87,57. Значения выбранного экологического показателя измеряются в тоннах.
Третий этап. Построение графиков функций f1(a) и f2(a) осуществляется через нахождение координат их точек. Область определения функций f1(a) и f2(a) в этой ситуации целесообразно задать интервалом [0,1; 700], так как P(X ≥ 0,1) = 1, а P(X ≥ 700) = 0.
Таблица 1
Значения случайной величины Х
|
0,23 |
8,61 |
13,33 |
20,19 |
39,98 |
63,05 |
95,3 |
149,27 |
494,85 |
|
0,96 |
8,99 |
13,55 |
21,06 |
45,06 |
63,83 |
96,47 |
150,68 |
673,09 |
|
1,1 |
9,37 |
14,08 |
24,22 |
46,26 |
66,57 |
98,08 |
151,7 |
689,68 |
|
1,42 |
9,38 |
15,63 |
26,8 |
48,66 |
67,19 |
100,46 |
214,06 |
|
|
2,87 |
10,34 |
15,89 |
30,03 |
52,32 |
74,8 |
102,76 |
224,74 |
|
|
4,13 |
10,45 |
16,13 |
31,87 |
53,53 |
79,13 |
119,56 |
226,61 |
|
|
5,15 |
11,35 |
16,54 |
33,7 |
55,32 |
79,49 |
125,2 |
304,02 |
|
|
5,45 |
12,38 |
16,84 |
36,38 |
58,3 |
80,1 |
135,38 |
311,19 |
|
|
5,64 |
12,59 |
19 |
36,44 |
61,64 |
80,21 |
140,8 |
323,22 |
|
|
6,77 |
12,96 |
19,52 |
38,82 |
62,7 |
85,64 |
141,51 |
336,02 |
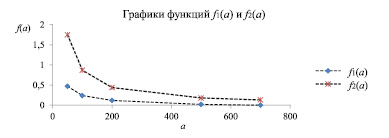
Рис. 1. Графические модели функций f1(a) и f2(a)
Значения функции f1(a) вычисляются по формуле
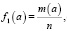 (3)
(3)
где m(a) – количество значений Х ≥ а (устанавливается непосредственным подсчетом).
Зафиксируем значения функций f1(a) и f2(a) в табл. 2, а их изображение представим на рис. 1.
Таблица 2
Значения функции f1(a) и f2(a)
|
№ п/п |
а |
m(a) |
f1(a) |
f 2(a) |
|
1 |
0,1 |
83 |
1 |
875,7 |
|
2 |
50 |
39 |
0,47 |
1,75 |
|
3 |
100 |
20 |
0,24 |
0,87 |
|
4 |
200 |
10 |
0,12 |
0,45 |
|
5 |
500 |
2 |
0,02 |
0,17 |
|
6 |
700 |
0 |
0 |
0,12 |
Четвертый этап. График функции f1(a) располагается ниже графика функции f2(a), следовательно, выполняется неравенство f1(a) ≤ f2(a). Это иллюстрирует тот факт, что вероятность P(X ≥ a) ограничивается сверху отношением МХ / а, согласно неравенству (1).
Иллюстрация вероятностных закономерностей неравенства Чебышева. Неравенство Чебышева утверждает, что, каково бы ни было положительное число а, вероятность P(|X – MX| ≥ a) того, что случайная величина Х абсолютно отклонится от своего математического ожидания не меньше чем на a, ограничена сверху величиной, равной отношению её дисперсии DX к квадрату числа a.
Первый этап. Запись неравенства Чебышева имеет вид [4, 9]
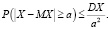 (4)
(4)
Дисперсия DX для дискретной случайной величины вычисляется по формуле [4, 9]
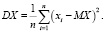 (5)
(5)
Если положительное число a выразить в единицах стандартного отклонения σ 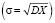 и ввести случайную величину
и ввести случайную величину 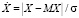 , то неравенство (4) можно записать в виде
, то неравенство (4) можно записать в виде
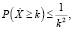 (6)
(6)
где k – кратность σ.
Исследуемые функциональные зависимости принимают вид t1(k) = P(X ≥ k) и t2(k) = 1/k2.
Второй этап. Преобразование совокупности статистических данных (табл. 1) для получения наглядной модели 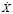 осуществляется через изменение всех значений Х. Дисперсия DX, вычисленная по формуле (5), равна 16780,39. Стандартное отклонение σ = 129,54. Значения случайной величины
осуществляется через изменение всех значений Х. Дисперсия DX, вычисленная по формуле (5), равна 16780,39. Стандартное отклонение σ = 129,54. Значения случайной величины 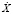 , упорядоченные по возрастанию, представлены в табл. 3.
, упорядоченные по возрастанию, представлены в табл. 3.
Минимальное и максимальное значения случайной величины 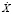 равны соответственно 0,015 и 4,648.
равны соответственно 0,015 и 4,648.
Третий этап. Построение графиков функций t1(k) и t2(k) осуществляется через нахождение координат их точек. Область определения функций задается интервалом [0,01; 5], так как 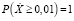 , а
, а 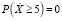 . Значения функции t1(k) вычисляются по формуле
. Значения функции t1(k) вычисляются по формуле
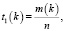 (7)
(7)
где m(k) – количество значений 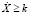 (устанавливается непосредственным подсчетом).
(устанавливается непосредственным подсчетом).
Зафиксируем значения функций t1(k) и t2(k) в табл. 4, а их изображение представим на рис. 2.
Четвертый этап. График функции t1(k) располагается ниже графика функции t2(k), следовательно, выполняется неравенство t1(k) ≤ t2(k). Это иллюстрирует тот факт, что вероятность 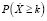 ограничивается сверху отношением 1/k2, согласно неравенству (6).
ограничивается сверху отношением 1/k2, согласно неравенству (6).
Таблица 3
Значения случайной величины 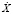
|
0,015 |
0,117 |
0,263 |
0,395 |
0,495 |
0,567 |
0,604 |
0,668 |
3,144 |
|
0,057 |
0,157 |
0,272 |
0,411 |
0,513 |
0,571 |
0,607 |
0,669 |
4,52 |
|
0,058 |
0,162 |
0,29 |
0,416 |
0,52 |
0,573 |
0,61 |
0,674 |
4,648 |
|
0,06 |
0,183 |
0,3 |
0,416 |
0,525 |
0,576 |
0,624 |
0,976 |
|
|
0,062 |
0,189 |
0,319 |
0,43 |
0,529 |
0,579 |
0,632 |
1,059 |
|
|
0,065 |
0,192 |
0,328 |
0,444 |
0,546 |
0,58 |
0,634 |
1,073 |
|
|
0,069 |
0,2 |
0,367 |
0,469 |
0,548 |
0,588 |
0,636 |
1,671 |
|
|
0,081 |
0,226 |
0,369 |
0,476 |
0,551 |
0,595 |
0,644 |
1,726 |
|
|
0,099 |
0,247 |
0,376 |
0,487 |
0,553 |
0,596 |
0,654 |
1,819 |
|
|
0,1 |
0,249 |
0,395 |
0,489 |
0,555 |
0,604 |
0,665 |
1,918 |
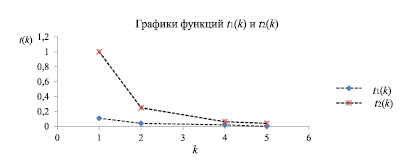
Рис. 2. Графические модели функций t1(k) и t2(k)
Таблица 4
Значения функции t1(k) и t2(k)
|
№ п/п |
k |
m(k) |
t1(k) |
t2(k) |
|
1 |
0,01 |
83 |
1 |
10000 |
|
2 |
1 |
9 |
0,11 |
1 |
|
3 |
2 |
3 |
0,04 |
0,25 |
|
4 |
4 |
2 |
0,02 |
0,0625 |
|
5 |
5 |
0 |
0 |
0,04 |
Выполнение студентами лабораторно-практического задания «Проверка адекватности математических моделей неравенств ЗБЧ» предусматривает активное использование электронных таблиц Excel [8]. Визуализация соотношений левых и правых частей в неравенствах Маркова и Чебышева осуществляется через изображение взаимного расположения графиков функциональных зависимостей. Возможности электронного процессора автоматизируют вычислительные процессы, необходимые для преобразования и упорядочивания статистических данных, нахождения значений характеристик случайных величин, построения графиков. Представленная технология организации учебной деятельности позволяет использовать данные материалы как методическое сопровождение при организации самостоятельной работы студентов.
Изучение неравенств Маркова и Чебышева студентами технических и экономических специальностей и направлений подготовки в вузовском курсе математики может осуществляться в следующей последовательности:
1) символьное и вербальное определение неравенств;
2) аналитическое доказательство для дискретных и непрерывных случайных величин;
3) выполнение представленного лабораторно-практического задания;
4) решение учебных задач.
Прохождение отмеченных этапов при изучении ЗБЧ требует активизации интеллектуальной деятельности студентов, что создает условия для развития их культуры мышления и творческих способностей в учебном процессе [7].
Заключение
Построение аналитико-синтетических рассуждений и умозаключений при доказательстве математических теорем и формул не всегда приводит студентов не математических специальностей и направлений подготовки в вузе к пониманию отображаемых в символьной форме существенных взаимосвязей объективной реальности, поэтому применение наглядных образов понятий и графических моделей расширяет систему дидактического сопровождения для познания окружающей действительности. Предложенное дополнение к методическим материалам по изучению ЗБЧ ставит своей целью включение студентов в исследовательскую деятельность, которая требует освоения теории и практики в диалектическом единстве.
Библиографическая ссылка
Куликова О.В., Куликова И.В. ИЛЛЮСТРАЦИЯ ВЕРОЯТНОСТНЫХ ЗАКОНОМЕРНОСТЕЙ ПРИ ИЗУЧЕНИИ НЕРАВЕНСТВ ЗАКОНА БОЛЬШИХ ЧИСЕЛ В ВУЗОВСКОМ КУРСЕ МАТЕМАТИКИ // Современные наукоемкие технологии. 2016. № 10-2. С. 342-346;URL: https://top-technologies.ru/ru/article/view?id=36332 (дата обращения: 07.02.2026).



