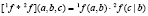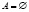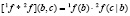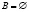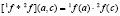Системология возникла для установления параметрически инвариантных характеристик систем и разработки на их базе автоматизированных методов решения системных задач. Крупнейшим специалистом по системологии признан почетный профессор Бингемтонского университета Джордж Клир [1, 6]. Исследования Дж. Клира показали, что методы системологии на основе анализа реконструктивных свойств позволяют установить глубокие внутренние связи между параметрами слабоформализованной системы. Особенно целесообразным видится их применение при исследовании систем, математическое моделирование которых по каким-либо причинам невозможно или затруднено. Кроме того, любая проблема, связанная со сложной системой, может быть представлена в виде общесистемной задачи посредством заложенного механизма абстрагирования/конкретизации. Таким образом, методами системологии могут быть решены задачи, возникающие в любой предметной области.
Одним из методов решения системных задач, предложенных им, является метод структурированных систем, который дополнительно дает возможность упростить исходную систему, а также и получить новые сведения, не содержащиеся в исходной системе.
Однако из-за критически быстрого роста количества реконструктивных гипотез, связанного с увеличением числа переменных n, определяющих состояние системы, основатель системологии не смог распространить разработанную им методику. Количества реконструктивных гипотез Gn для систем различной размерности представлены в табл. 1 (каждая реконструктивная гипотеза представляет собой совокупность структурированных систем).
Таблица 1
Число реконструктивных гипотез
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|
Gn |
1 |
2 |
9 |
114 |
6894 |
7785062 |
Целью исследования является уменьшение вычислительной сложности методов системологии и реализация возможности их применения для решения системных задач.
Для достижения поставленной цели впервые предложена модификация метода структурированных систем Дж. Клира [3, 4].
Модифицированный метод структурирования систем предполагает модификацию алгоритмов решения основных взаимодополняющих задач системологии: задачи реконструкции и задачи идентификации [2, 5].
В общем виде модифицированный метод структурированных систем состоит из следующих этапов:
1. Задать множество целевых переменных 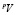 .
.
2. Задать 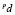 – процент допустимого отклонения информационного расстояния.
– процент допустимого отклонения информационного расстояния.
3. Задать Δ– значение допустимой погрешности согласованности.
4. Выполнить процедуру поиска решеток уточнения.
5. Выполнить базовую процедуру соединения для структурированных систем, соответствующих каждой решетке.
6. Если не найдена несмещенная реконструкция, выполнить итеративную процедуру соединения на основе функции поиска решеток уточнения.
7. Если не найдена несмещенная реконструкция, система не согласована, реконструкции не существует.
8. Выполнить отбраковку несодержательных или неудовлетворяющих условиям исследователя реконструктивных гипотез и соответствующих им решеток уточнения.
9. Если дальнейшее уточнение возможно, перейти на шаг 4.
10. Вывод на основе реконструктивного анализа.
Решение системных задач в модифицированном методе начинается с постановки и решения задачи реконструкции.
Задача реконструкции формулируется следующим образом. Дана система с поведением, рассматриваемая как полная система. Требуется определить, какие наборы ее подсистем (каждый такой набор рассматривается как гипотетическая реконструкция) подходят для реконструкции заданной системы с заданной точностью, причем реконструкция должна производиться только по той информации, которая содержится в этих подсистемах.
Полная система, набор всех ее реконструктивных гипотез с отношением уточнения, образующим решетку, называется решеткой уточнения. Решетка уточнения может быть получена выполнением одной универсальной процедуры уточнения для любой указанной реконструктивной гипотезы. Реконструктивные гипотезы формируются из полной системы в несколько шагов и подразделяются на уровни уточнения, включающие решетки уточнения.
Любая реконструктивная гипотеза полностью описывается:
1) семейством подмножеств входящих в нее переменных;
2) функциями поведения, соответствующими отдельным подмножествам переменных.
Если опустить свойство 2, то свойство 1 определяет класс инвариантности реконструктивных гипотез, отличающихся друг от друга только функциями поведения их элементов. Этот класс инвариантности называется структурой. Так как отдельная реконструктивная гипотеза представляет собой структурированную систему, то структура – это свойство структурированной системы, инвариантное относительно изменения функций поведения ее элементов.
Для множества переменных S множество структур, представляющих все реконструктивные гипотезы любой полной системы, определенной на S, состоит из семейств подмножеств S, удовлетворяющих условиям неизбыточности и покрытия. Обозначим все множества переменных одной мощности n, общим множеством структур Gn, определенным на множестве Nn натуральных чисел. Формально для любого 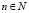 ,
, 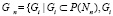 – удовлетворяет условиям неизбыточности и покрытия}, где P(Nn) – множество всех подмножеств множества Nn.
– удовлетворяет условиям неизбыточности и покрытия}, где P(Nn) – множество всех подмножеств множества Nn.
В этом формальном определении через Gi обозначены элементы Gn, являющиеся наиболее общими структурами, рассматриваемыми при решении задачи реконструкции. Индекс i идентифицирует структуры из Gn, и обычно 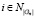 . Структуры из множеств Gn называются G-структурами.
. Структуры из множеств Gn называются G-структурами.
Реконструктивные гипотезы могут изучаться в виде абстрактных структур. Структура из Gn становится конкретной реконструктивной гипотезой, когда интерпретируется в контексте сравнимой с ней определенной полной системы с поведением (т.е. системы с n переменными).
Основным вопросом задачи реконструкции является разработка эффективных вычислительных процедур, допускающих представление, оценку и сравнение реконструктивных гипотез, представленных всеми структурами для заданного множества переменных. Для ее успешного решения требуется использовать соответствующее упорядочение и классификацию структур.
Определим упорядочение структур. Пусть даны две структуры 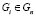 и
и 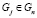 . Будем называть Gi уточнением Gj (Gj укрупнением Gi), тогда и только тогда, когда для любого
. Будем называть Gi уточнением Gj (Gj укрупнением Gi), тогда и только тогда, когда для любого 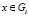 существует
существует 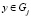 , такое, что
, такое, что 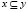 ; пусть
; пусть 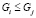 означает, что Gi является уточнением Gj.
означает, что Gi является уточнением Gj.
Gi называется непосредственным уточнением Gj тогда и только тогда, когда не существует 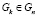 , такого, что
, такого, что 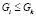 и
и 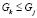 . Для заданной структуры
. Для заданной структуры 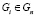 структурное соседство определяется как множество всех непосредственных уточнений и непосредственных укрупнений Gi в Gn. Рассмотренные структуры образуют решетку уточнения G-структур, которая может быть получена в результате неоднократного выполнения процедуры, порождающей все непосредственные уточнения для любой структуры из решетки. Одной из таких процедур является уточняющая процедура для G-структур (RG-процедура).
структурное соседство определяется как множество всех непосредственных уточнений и непосредственных укрупнений Gi в Gn. Рассмотренные структуры образуют решетку уточнения G-структур, которая может быть получена в результате неоднократного выполнения процедуры, порождающей все непосредственные уточнения для любой структуры из решетки. Одной из таких процедур является уточняющая процедура для G-структур (RG-процедура).
При решении задачи реконструкции выполняется три набора процедур:
– процедуры порождения реконструктивных гипотез;
– процедуры оценки и сравнения порожденных реконструктивных гипотез с точки зрения целей задачи реконструкции;
– процедуры, которые на соответствующих этапах принимают решение о том, какие из порожденных реконструктивных гипотез будут включены во множество решений, какие использованы для дальнейшего порождения реконструктивных гипотез и должен ли процесс решения продолжаться или закончиться.
Для реализации указанных наборов процедур, уменьшения вычислительной сложности за счет сокращения количества реконструктивных гипотез с сохранением упорядочения решеток по степени (уровню) уточнения был разработан модифицированный алгоритм RG-процедуры. Рассмотрим описание модифицированного алгоритма RG-процедуры:
1) задать G-структуры
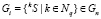 ;
;
2) присвоить k = 0;
3) если 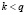 , то
, то 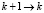 , иначе перейти на шаг 6;
, иначе перейти на шаг 6;
4) если 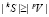 и
и 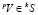 , то
, то
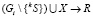 ,
,
где 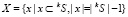 ; иначе перейти на шаг 3;
; иначе перейти на шаг 3;
5) 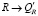 , где
, где 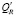 – неизбыточный аналог R, Qf – соответствующее
– неизбыточный аналог R, Qf – соответствующее 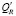 распределение вероятности и
распределение вероятности и
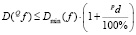 ,
,
записать 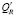 в качестве непосредственного уточнения Gi, перейти на шаг 3;
в качестве непосредственного уточнения Gi, перейти на шаг 3;
6) конец.
Модифицированная процедура поиска решеток уточнения предполагает учет целевых переменных 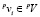 и значения
и значения 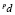 . Учет целевых переменных обеспечивает на каждом уровне уточнения хотя бы один элемент Gi общих структур
. Учет целевых переменных обеспечивает на каждом уровне уточнения хотя бы один элемент Gi общих структур 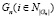 , содержащий идентификаторы из набора
, содержащий идентификаторы из набора 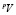 . Если данное требование не выполняется, решетка уточнения Gi исключается и не участвует в дальнейшей процедуре поиска. Данное требование позволяет ощутимо сократить количество реконструктивных гипотез, за счет отбраковки гипотез, не интересующих исследователя.
. Если данное требование не выполняется, решетка уточнения Gi исключается и не участвует в дальнейшей процедуре поиска. Данное требование позволяет ощутимо сократить количество реконструктивных гипотез, за счет отбраковки гипотез, не интересующих исследователя.
Использование ограничения на информационное расстояние функции поведения f структурированной системы, соответствующей решетки уточнения, подразумевает выбор и уточнение тех решеток, информационное расстояние D(f) которых удовлетворяет условию
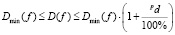 , (1)
, (1)
где D(f) – информационное расстояние для реконструктивной гипотезы на конкретном уровне уточнения;
Dmin(f) – минимальное информационное расстояние на конкретном уровне уточнения;
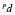 – допустимый исследователем процент отклонения от минимального информационного расстояния.
– допустимый исследователем процент отклонения от минимального информационного расстояния.
Для вероятностных систем информационное расстояние выражается известной формулой:
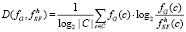 , (2)
, (2)
где 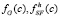 – значение вероятности для состояния
– значение вероятности для состояния 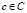 в исходной полной системе G и в реконструкции полной системы SF, соответственно;
в исходной полной системе G и в реконструкции полной системы SF, соответственно;
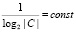 – нормирующий коэффициент, благодаря которому информационное расстояние обладает свойством:
– нормирующий коэффициент, благодаря которому информационное расстояние обладает свойством: 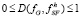 .
.
Для того чтобы проанализировать полученные на каждом этапе решетки уточнения, необходимо вычислить соответствующие им информационные расстояния. Из формулы (2) видно, что информационное расстояние вычисляется для реконструкции полной системы. Решетка уточнения представляет собой набор подсистем (структурированную систему). Чтобы перейти от решетки уточнения к реконструкции полной системы необходимо решить задачу идентификации, то есть задачу нахождения полной системы на основе имеющихся подсистем.
Задача идентификации содержит в себе две подзадачи. Первая связана с нахождением множества всех полных систем, представленных структурированной системой. Вторая – это задача выбора из реконструктивного семейства такой полной системы, которая задает лучшую гипотезу относительно реальной полной системы. Для выбора единственной системы из реконструктивного семейства применяется два подхода:
1. Поиск несмещенной реконструкции – полной системы, которая опирается на всю информацию, содержащуюся в структурированной системе, и не использует никакой дополнительной информации;
2. Поиск реконструкции с наименьшим риском – полной системы, для которой минимизирована наибольшая возможная ошибка, т.е. обобщенное расстояние между распределениями реконструированной и истинной системы.
Несмещенная реконструкция, если она существует, находится с помощью базовой процедуры соединения, комбинирующей функции поведения элементов заданной структурированной системы.
Рассмотрим принцип базовой процедуры соединения. Пусть дана структурированная система с поведением SF. Требуется выполнить операцию соединения для двух ее подсистем, описываемых функциями 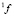 и
и 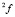 с множеством выборочных переменных
с множеством выборочных переменных 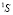 и
и 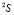 соответственно. Операция соединения обозначается как
соответственно. Операция соединения обозначается как 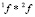 . Все множество выборочных переменных, входящих в состав этих двух подсистем, делится на три подмножества:
. Все множество выборочных переменных, входящих в состав этих двух подсистем, делится на три подмножества:
A – множество выборочных переменных, входящих только в первую подсистему;
B – множество выборочных переменных, общих для обеих подсистем;
C – множество выборочных переменных, входящих только во вторую подсистему.
Обозначая буквами a, b, c отдельные состояния выборочных переменных из множеств A, B, C соответственно, представим результат процедуры базового соединения в виде табл. 2. Для определения несмещенной реконструкции операция базового соединения должна быть выполнена для пар элементов этой системы. При каждом ее выполнении два элемента объединяются в новую структурированную систему. Эта операция называется базовой процедурой соединения.
Таблица 2
Результат базовой процедуры соединения 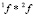
|
Условие |
Вероятностная функция распределения |
|
Общий случай |
|
|
|
|
|
|
|
Алгоритм базовой процедуры соединения. Дана локально согласованная структурированная система с поведением SF (вероятностная) с функциями поведения 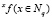 . Для получения соединения
. Для получения соединения 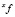 для всех
для всех 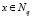 необходимо выполнить следующие шаги:
необходимо выполнить следующие шаги:
1) присвоить 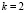 и
и 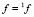 ;
;
2) произвести соответствующую группировку аргументов 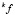 и f, выполнить соответствующий вариант операции соединения
и f, выполнить соответствующий вариант операции соединения 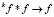 (обычной или вырожденной);
(обычной или вырожденной);
3) если 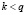 , то
, то 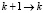 , и перейти на шаг 2;
, и перейти на шаг 2;
4) стоп.
Если результат применения базовой процедуры соединения 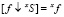 для всех
для всех 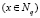 , то это несмещенная реконструкция, в противном случае f не соответствует заданной структурированной системе и должна быть уточнена итеративной процедурой соединения.
, то это несмещенная реконструкция, в противном случае f не соответствует заданной структурированной системе и должна быть уточнена итеративной процедурой соединения.
Итеративная процедура соединения. Дана локально согласованная структурированная система с поведением SF с вероятностными функциями поведения 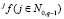 . Также дана функция f, полученная с помощью базовой процедуры соединения, примененной к SF, и число
. Также дана функция f, полученная с помощью базовой процедуры соединения, примененной к SF, и число 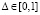 . Требуется с точностью до Δ определить функцию поведения несмещенной реконструкции.
. Требуется с точностью до Δ определить функцию поведения несмещенной реконструкции.
Таблица 3
Матрица данных
|
v1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
v2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
0 |
|
v3 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
v4 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
|
N(c) |
21 |
21 |
28 |
14 |
19 |
37 |
34 |
22 |
36 |
17 |
23 |
40 |
10 |
11 |
36 |
3 |
5 |
23 |
61 |
|
Продолжение табл. 3 |
|||||||||||||||||||
|
v1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
|
v2 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
0 |
0 |
|
v3 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
v4 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
|
N(c) |
23 |
17 |
78 |
46 |
43 |
43 |
35 |
40 |
48 |
45 |
86 |
26 |
18 |
54 |
15 |
25 |
62 |
13 |
9 |
|
Продолжение табл. 3 |
|||||||||||||||||||
|
v1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
|
v2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
0 |
0 |
0 |
|
v3 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
v4 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
|
N(c) |
10 |
20 |
23 |
20 |
8 |
8 |
12 |
10 |
22 |
24 |
6 |
7 |
9 |
7 |
10 |
21 |
18 |
6 |
7 |
|
Окончание табл. 3 |
|||||||||||||||
|
v1 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
v2 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
|
v3 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
v4 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
|
N(c) |
57 |
23 |
13 |
15 |
13 |
13 |
31 |
21 |
13 |
7 |
5 |
11 |
5 |
6 |
13 |
Модифицированный алгоритм итеративной процедуры соединения:
1) присвоить j = 0, i = 1 и f0 = f;
2) сделать соответствующее разбиение аргументов 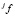 и
и 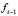 и выполнить операцию соединения
и выполнить операцию соединения 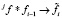 для вырожденного случая;
для вырожденного случая;
3) если 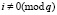 , то
, то 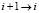 ,
, 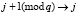 , перейти на шаг 2;
, перейти на шаг 2;
4) если 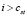 , то перейти на шаг 6;
, то перейти на шаг 6;
5) если 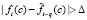 для какого-то
для какого-то 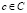 , то
, то 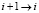 ,
, 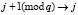 , и перейти на шаг 2;
, и перейти на шаг 2;
6) конец.
Если после выполнения итеративной процедуры соединения сумма 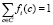 , то
, то 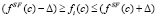 , для всех
, для всех 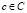 . В противном случае данная структурированная система SF глобально не согласована и реконструкции для нее не существует, а следовательно, SF бессодержательна.
. В противном случае данная структурированная система SF глобально не согласована и реконструкции для нее не существует, а следовательно, SF бессодержательна.
Для оптимизации работы итеративной процедуры соединения значение допустимой погрешности согласованности, Δ задается исследователем, что позволяет, при желании, расширить поиск оптимальной реконструкции. В итеративную процедуру также было введено ограничение на количество шагов итеративной функции поведения – cst, что позволило определить момент завершения процедуры (реконструктивную гипотезу не удается получить – подсистемы не совместимы).
Модифицированный алгоритм решает указанные ранее проблемы, возникающие при использовании алгоритма Дж. Клира. На основе полученного алгоритма был разработан вычислительный алгоритм и его программная реализация, на которую получено свидетельство о государственной регистрации (РФ, номер свидетельства: № 2015618132). Программа работает в операционных системах Windows ХР/Vista/7/8/8.1/10.
Рассмотрим пример, который исследовал Дж. Клир [2]. Пример содержит данные, собранные в процессе изучения мнения о жилищных условиях в Копенгагене. Был опрошен 1881 квартиросъемщик, об их отношении к жилищным условиям, о контактах с другими квартиросъемщиками, мнение об их влиянии на содержание жилья. Одновременно с этим регистрировался тип дома каждого квартиросъемщика. Таким образом, было выделено четыре переменных:
v1 – тип дома (0 – многоквартирный, 1 – меблированный, 2 – отдельный дом, 3 – дом с общими боковыми стенами);
v2 – мнение о влиянии на содержание жилья (0 – низкое, 1 – среднее, 2 – высокое);
v3 – степень контакта с соседями (0 – низкая, 1 – высокая);
v4 – степень удовлетворенности жилищными условиями (0 – низкая, 1 – средняя, 2 – высокая).
В табл. 3 приведены состояния переменных и частоты их встречаемости N(c).
Таблица 4
Информационные расстояния
|
Степень уточнения |
Наборы |
Расстояния |
|
2 |
123 / 124 / 134 / 234 |
0,000390 |
|
3 |
123 / 124 / 134 |
0,000470 |
|
3 |
123 / 124 / 234 |
0,001120 |
|
3 |
123 / 134 / 234 |
0,001880 |
|
3 |
124 / 134 / 234 |
0,000700 |
|
4 |
123 / 124 / 34 |
0,001160 |
|
4 |
123 / 134 / 24 |
0,001970 |
|
4 |
124 / 134 / 23 |
0,000960 |
|
5 |
124 / 134 |
0,002350 |
|
5 |
124 / 13 / 23 / 34 |
0,001660 |
|
5 |
134 / 12 / 23 / 24 |
0,002120 |
|
6 |
124 / 13 / 23 |
0,002710 |
|
6 |
124 / 13 / 34 |
0,002980 |
|
6 |
124 / 23 / 34 |
0,004850 |
|
6 |
12 / 13 / 14 / 23 / 24 / 34 |
0,003130 |
|
7 |
124 / 13 |
0,003810 |
|
7 |
124 / 23 |
0,005420 |
|
7 |
12 / 13 / 14 / 23 / 24 |
0,004960 |
|
7 |
124 / 34 |
0,006080 |
|
7 |
12 / 13 / 14 / 24 / 34 |
0,004580 |
|
8 |
124 / 3 |
0,006610 |
|
8 |
12 / 13 / 14 / 24 |
0,005440 |
|
9 |
12 / 13 / 14 |
0,012430 |
|
9 |
12 / 13 / 24 |
0,009440 |
|
9 |
12 / 14 / 24 / 3 |
0,008320 |
|
9 |
13 / 14 / 24 |
0,006100 |
|
10 |
13 / 14 / 2 |
0,013840 |
|
10 |
13 / 24 |
0,010640 |
|
10 |
14 / 24 / 3 |
0,011240 |
|
11 |
24 / 1 / 3 |
0,013360 |
|
11 |
14 / 2 / 3 |
0,015560 |
|
12 |
1 / 2 / 3 / 4 |
0,020770 |
Цель эксперимента: изучение влияния типа дома, мнения о содержании жилья, степени контакта с соседями на степень удовлетворенности жилищными условиями. Таким образом, целевая переменная 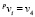 .
.
Установим параметры вычислений, например, 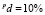 , Δ = 0,00005.
, Δ = 0,00005.
В результате работы программы получен вывод о решетках уточнений и соответствующих информационных расстояниях (табл. 4): полужирным шрифтом выделены минимальные расстояния, курсивом – расстояния, удовлетворяющие параметру 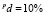 .
.
На основании приведенных данных можно сделать вывод, что основные факторы, влияющие на степень удовлетворенности жилищными условиями, – это тип дома и мнение о содержании жилья. При этом второй фактор влияет сильнее. Фактор «степень контакта с соседями» также влияет на степень удовлетворенности жилищными условиями, но слабее остальных. Каждый полученный набор представляет собой вариант декомпозиции системы с учетом указанных взаимосвязей.
Таблица 5
Сравнение числа реконструктивных гипотез для системы из четырех переменных
|
Метод структурирования систем |
Gn |
|
Метод Дж. Клира |
114 |
|
Метод, модифицированный автором |
32 |
Число реконструктивных гипотез, полученных модифицированным методом, значительно меньше числа реконструктивных гипотез, полученных методом Дж. Клира (табл. 5), что позволяет решать поставленные задачи быстрее и с меньшей вычислительной нагрузкой.
Изложенный модифицированный метод позволил многократно сократить вычислительную сложность оригинального метода, что сделало возможным его программную реализацию и применение для решения системных задач.
Библиографическая ссылка
Синельникова Т.И., Швецова Н.А. МОДИФИКАЦИЯ МЕТОДА СТРУКТУРИРОВАННЫХ СИСТЕМ ДЖ. КЛИРА // Современные наукоемкие технологии. 2016. № 10-2. С. 298-303;URL: https://top-technologies.ru/ru/article/view?id=36323 (дата обращения: 21.02.2026).