Известно, что в современной методологии анализа сложных систем, при рассмотрении динамических моделей и построении общих законов поведения и управления, с целью нахождения новых закономерностей и характеристик сложной системы, предлагается проведение аналогий между процессами, относящимися к различным областям науки. В частности, результаты современных исследований показали, что характеристики физико-механики сердечно-сосудистой системы, близкие к результатам физиологических экспериментов достигаются в приближении, что миокард сердца имеет топологию Мебиуса [1, 7, 8]. Это позволяет, для моделирования электрической активности возбудимых волокон сердца, использовать приближение в виде магнитопровода, выполненного из ферромагнитного материала в виде тора с поверхностью Мебиуса и локальным расположением катушки намагничивания [2, 3, 5]. Для уменьшения затрат на ревизию магнитопроводов с точки зрения развития дефектов как аналогов патологий актуальным представляется исследовать отклик при внешнем электромагнитном воздействии.
Научная новизна
Целью исследований является экспериментальная проверка на образцах-имитаторах возможности оценки отклонения топологии магнитопровода от топологии тора с поверхностью Мебиуса по результатам изменения активного сопротивления и индуктивности катушки намагничивания при внешнем электромагнитном воздействии с частотой 50–15000 Гц различной интенсивности. Полученные результаты можно использовать для моделирования дефектов магнитопровода как аналогов патологий миокарда сердца, а также использовать для формирования эталонных сигналов при различных повреждениях исследуемых образцов.
Материалы и методы исследования
Для оценки влияния неориентированной поверхности выполним, в частотном диапазоне 50–15000 Гц, в соответствии с известной методологией [6] определение сравнительных показателей электромагнитных свойств магнито-мягких ферромагнетиков при использовании их в качестве материалов замкнутых стержневых сердечников, в которых топология замкнутого магнитного контура при одинаковой длине его средней линии и одинаковом квадратном сечении стержней выполнена в двух топологических формах: к – контрольный образец: внешние образующие всех стержней лежат в общих плоскостях (стандартное исполнение, как у обычных сердечников); м – экспериментальный образец: образующие двух замыкающих стержней (двух ярём) перекручены вокруг осей стержня каждая на 90 градусов, образуя, в совокупности друг с другом и с недеформированными стержнями поверхности Мёбиуса правого и левого спинов в системе замкнутого магнитопровода.
Магнитопровод экспериментальных образцов выполнен из ферромагнитного материала типа Magnifer с габаритными размерами: внутренний радиус 40 мм, внешний радиус 50 мм, сечение прямоугольное 10 мм. Ток заданной частоты f и силы тока протекает через катушку с числом витков 100. Расчетная электрическая схема эксперимента представлена на рис. 1.
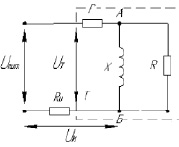
Рис. 1. Расчетная электрическая схема эксперимента
Условные обозначения: r – активное сопротивление намагничивающей обмотки катушки (сопротивление меди); RИ – калиброванное активное сопротивление для измерения тока;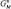 
, 
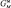– активная проводимость катушки, обусловленная вихревыми токами; 
, 
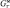– активная проводимость катушки, обусловленная потерями на перемагничивание (магнитным гистерезисом); 
, 
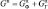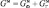– активная проводимость намагничивающей катушки; Bк, Bм – индуктивная проводимость намагничивающей катушки; Lк, Lм – индуктивность намагничивающей катушки. В принятых обозначениях верхний индекс к, м соответствует данным при использовании контрольного (к) и мёбиусного (м) сердечника
Величина относительного изменения составляющей активного сопротивления намагничивающей катушки, обусловленная свойствами мёбиусного сердечника по сравнению с составляющей активного сопротивления намагничивающей катушки, обусловленной свойствами контрольного сердечника:
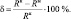(1)
Исходные расчетные соотношения получаются из двух базовых выражений для комплекса электрического импеданса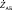 
и для полного электрического импеданса катушки 
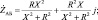(2)
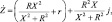(3)
где R – активная составляющая сопротивления участка АБ (рис. 1), обусловленная свойствами сердечника; X – реактивная (индуктивная) составляющая сопротивления участка АБ, обусловленная свойствами сердечника.
Перепишем выражения (2), (3) в виде системы алгебраических уравнений
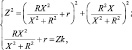(4)
где k = cos(2πfτ) – коэффициент мощности катушки, определяемый через установленный параметр f и измеренное значение временного сдвига τ между величинами UТ и UИ.
Найдем в общем виде решение системы (4):
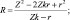
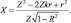(5)
Модуль Z полного электрического импеданса катушки выражается через измеряемые величины UТ, UИ, RИ следующим образом
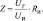(6)
Модуль индуктивного сопротивления катушки намагничивания:
X = 2πfL, (7)
где L – индуктивность катушки намагничивания с сердечником.
Из выражения (4) с учетом (5)–(7) получим:
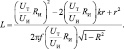(8)
Тогда выражение (4) принимает вид:
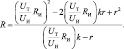(9)
Формулы (8) и (9) являются базовыми расчетными формулами.
Результаты исследования и их обсуждение
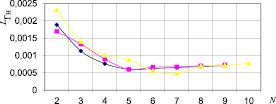
Результаты измерений и расчетов (1)–(9) приведены на рис. 2–4. На рис. 2, 3 приведены зависимости активного сопротивления потерь R и индуктивности L от частоты, форма которых является характерной и не изменяется во всем диапазоне 0,005…0,18 А протекающего через катушку силы тока.
Видно, что с ростом частоты сопротивление R возрастает, а индуктивность L уменьшается. Характер и форма изменения зависимостей, приведенные на рис. 2, при изменении силы остаются аналогичными во всем диапазоне изменения силы тока текущего через катушку (рис. 3).
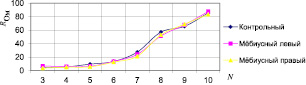
a
б
Рис. 2. Зависимость изменения активной (a) и индуктивной (б) составляющих сопротивления намагничивающей катушки при I = 0,005 А, N – частота равная значениям: 1 – 50 Гц; 2 – 100 Гц; 3 – 250 Гц; 4 – 500 Гц; 5 – 1000 Гц; 6 – 2500 Гц; 7 – 5000 Гц; 8 – 10000 Гц; 9 – 12000 Гц; 10 – 15000 Гц
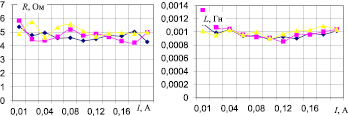
Рис. 3. Зависимость изменения активной (a) и индуктивной (б) составляющих сопротивления намагничивающей катушки при f = 500 Гц
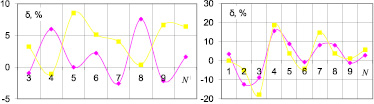
а б
Рис. 4. Относительная разница потерь: а – I = 0,01 А; б – I = 0,17 А
Известно, что активное сопротивление и индуктивность не должны существенно изменяться с изменением частоты [4]. Таким образом, характер зависимости активной и индуктивной составляющих сопротивления катушки от частоты, представленный на рис. 2, 3, свидетельствует о том, что в результате измерений и расчетов, произведенных в соответствии с канонической схемой замещения катушки, по всей видимости, не учтена межвитковая емкость обмотки катушки, обуславливающая уменьшение расчетного значения индуктивности с увеличением частоты, по мере удаления частоты от ее резонансного значения. Это подтверждается характером зависимости, представляющим собою ниспадающую ветвь «резонансного колокола». Однако, поскольку целью методики эксперимента является относительное сравнение свойств магнитопроводов с различной топологией, выявленная проблема верифицируемости расчетной схемы не уменьшает ценности приведенных на графиках экспериментальных данных. Рассмотрим влияние топологии магнитопровода на отклик при внешнем электромагнитным воздействии (рис. 4).
Видно, разница в уровне потерь в базовом и мебиусном варианте магнитопровода зависит от частоты и может достигать 15 %, что превышает погрешность измерений. Это позволяет предположить связь с процессами, связанными с распространением магнитного потока в магнитопроводе. Косвенно это подтверждается тем, что разница в уровне потерь зависит как от спина мебиусного магнитопровода, так и от уровня магнитного потока в магнитопроводе, а также тем, что с увеличением тока намагничивания и, как следствие, магнитного потока, наблюдается рост разницы и унижается чувствительность от спина магнитопровода.
Заключение
Показано по результатам экспериментального исследования на образцах имитаторах влияния топологии магнитопровода на отклик при внешнем электромагнитном воздействии, что разница в уровне потерь в базовом и мебиусном варианте магнитопровода достигает 15 %. Это позволяет предположить, что выполнение оценки функционального резерва деятельности сердца может быть определено экспериментально по результатам существующих методов диагностики в условиях внешнего электромагнитного воздействия путем сравнения соответствия топологии миокарда и топологии Мебиуса.
Библиографическая ссылка
Арутюнов Ю.А., Дробязко А.А., Крылов А.И., Чащин Е.А., Шашок П.А., Шилов И.В. ВЛИЯНИЕ ТОПОЛОГИИ МАГНИТОПРОВОДА НА ОТКЛИК ПРИ ВНЕШНЕМ ЭЛЕКТРОМАГНИТНОМ ВОЗДЕЙСТВИИ // Современные наукоемкие технологии. – 2016. – № 10-1. – С. 29-32;URL: https://top-technologies.ru/ru/article/view?id=36273 (дата обращения: 19.04.2024).