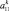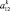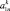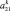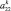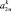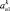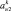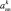Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хачумов М.В. 1

---

1 ФГУ «Федеральный исследовательский центр “Информатика и управление” Российской академии наук»

Настоящая статья посвящена разработке метода сравнения иерархических медицинских технологических процессов (МТП), используемых для персонифицированного лечения пациентов. МТП представлен в виде многоуровневого ориентированного графа, в котором каждый уровень представляет собой отдельный крупный этап лечения. При известных значениях расстояний между отдельными уровнями, записанными в общую матрицу, определение расстояния между двумя МТП сводится к поиску кратчайшего пути, для вычисления которого предлагается воспользоваться методом динамического программирования. Расстояние между двумя иерархическими структурами, в общем случае, является составным и определяется сверткой расстояний по шкалам наименований и времени. Для установления весов свертки привлекаются эксперты, которые оценивают важность каждого критерия. Рассмотрен пример сравнения процессов лечения заболевания бронхиальной астмой трех пациентов.

Статья в формате PDF

0 KB

технологический процесс

метрика

иерархические структуры

динамическое программирование

персонифицированное лечение

1. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. – Новосибирск: Изд-во Ин-та математики, 1999. – 270 с.

2. Молодченков А.И. Автоматический синтез типовых схем лечения на основе медицинских данных // Информационные технологии в медицине: Труды X Ежегодной специализированной конференции и выставки. – М.: Консэф, 2009. – C. 148–156.

3. Молодченков А.И., Хачумов М.В., Яшина Л.П. Подходы к анализу отклонений медицинских технологических процессов // Труды Института Системного Анализа РАН. – 2016. – № 2. – C. 74–84.

4. Назаренко Г.И., Осипов Г.С. Основы теории медицинских технологических процессов. – Ч. 1. – М.: ФИЗМАТЛИТ, 2005. – 144 с.

5. Назаренко Г.И., Осипов Г.С. Основы теории медицинских технологических процессов. – Ч. 2. Исследование медицинских технологических процессов на основе интеллектуального анализа данных. – М.: ФИЗМАТЛИТ, 2006. – 144 с.

6. Саати Т. Принятие решений. Метод анализа иерархий: пер. с англ. – М.: Радио и связь, 1989. – 316 с.

7. Хачумов В.М. Основные принципы моделирования сложных систем и процессов. Учебное пособие. – М.: Изд-во Российского университета дружбы народов, 2013. – 141 с.

8. Хачумов М.В. Метод оценки отклонения медицинского технологического процесса от стандарта лечения // Сборник научных трудов по материалам VII международной научно-практической конференции (Белгород, 31 октября 2015). – 2015. – № 7. – C. 132–137.

9. Яковлев В.Б. Автоматизированное управление технологическими процессами: Учебное пособие. – Л.: Изд-во Ленингр. ун-та, 1988. – 224 с.

10. Ing-Jr Ding, Chih-Ta Yen, Yen-Ming Hsu. Developments of machine learning schemes for dynamic time-wrapping-based speech recognition // Mathematical Problems in Engineering. – 2013.

В настоящее время накоплены большие объемы знаний в области лечения пациентов по различным нозологиям. Знания, хранящиеся в виде последовательностей действий лечащего врача и фиксации исходов, могут быть объединены и формализованы, например, в виде обобщенных графов лечения [2, 4, 5]. Наличие подобных баз знаний и обобщенного графа в конкретной области дает возможность лечащему врачу проводить изучение историй болезней, выполнять сравнение путей лечения пациентов и, соответственно, повышать свое мастерство, а также позволяет избежать грубых ошибок. Необходимость выбора пути лечения возобновляется с каждым новым пациентом, обладающим помимо общих черт, присущих всем пациентам с данной нозологией, еще и индивидуальными специфическими особенностями организма, что может привести к отклонениям от известных путей лечения и, соответственно, пополнить базу знаний новым прецедентом. Здесь важно знать, в какой степени конкретный процесс отличается от уже имеющегося прецедента в базе знаний. Естественно предположить, что с увеличением числа прецедентов базы знаний становится весьма высокой вероятность наличия в базе повторяющихся участков или даже полной технологической цепочки адекватной процессу лечения конкретного пациента. Вопросы построения метрик и измерения расстояний между двумя последовательностями – простейшими медицинскими технологическими процессами (МТП), рассматривались автором, например, в работах [3, 8]. В настоящей работе, являющейся развитием ранее предложенного подхода, проводится обобщение способов и выбор инструментальных средств корректного сопоставления более сложных МТП, представленных в виде иерархических структур специального вида.

Постановка задачи

Положим, что МТП представлен в виде многоуровневого ориентированного графа, в котором каждый уровень представляет собой отдельный крупный этап лечения. Каждый этап детализируется в виде последовательности выполненных операций, т.е. ориентированной веткой графа. Пример подобного ориентированного гиперграфа, отражающего процесс лечения бронхиальной астмы, в обобщенном виде приведен на рисунке.

В табл. 1 приведены названия операций процесса лечения бронхиальной астмы, показанных на рисунке.

Заметим, что различные МТП одной нозологии могут отличаться по числу уровней, по времени и длительности их исполнения [2, 4, 5]. В свою очередь отдельные уровни МТП могут отличаться как по составу и числу операций, так и по порядку выполнения операций. Эта особенность создает предпосылки для выбора адекватных методов сравнения отдельных этапов МТП между собой и иерархических структур в целом. С учетом указанных особенностей расстояние между двумя иерархическими структурами будет являться составным и определяться сверткой расстояний по шкалам наименований и времени. Процесс сравнения и измерения расстояний между МТП носит субъективный характер и зависит от выбора весовых коэффициентов и метрик, определяемых экспертами.

Предлагаемый метод решения

Представим МТП в виде последовательности этапов A = {a1, a2, ..., an}, называемых иначе уровнями иерархии. Каждый k-й уровень характеризуется временем и длительностью выполнения. Будем полагать, что медицинские мероприятия на каждом k-м уровне иерархии образуют технологическую цепочку вида 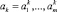, характеризуемую определенным составом операций и удовлетворяющую определенным требованиям и ограничениям следования [1, 6]. Выберем в качестве объектов исследования два МТП A = {a1, a2, ..., an} и B = {b1, b2, ..., bm}, причем в общем случае n ≠ m.

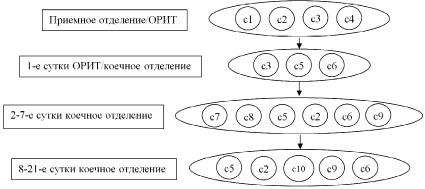
Процесс лечения бронхиальной астмы

Таблица 1

Название операций процесса лечения бронхиальной астмы

Рассмотрим вначале шкалу наименований (scale items), в соответствии с которой элементы отдельной технологической цепочки медицинских мероприятий (операций) выступают в отношениях друг к другу: «равно (совпадает)» и «не равно (не совпадает)», т.е. «=» или «≠». Выберем два уровня k и p, соответственно МТП A и B. Пусть например, 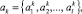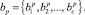Для корректного сравнения количество элементов в ak и bp должно быть одинаково. В этом случае выбирается N = max(1, c), и если 1 < c, то 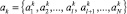. То есть происходит дополнение короткой последовательности некоторыми псевдооперациями 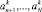. Будем в качестве меры рассогласования между уровнями иерархий k и p двух МТП A и B использовать правило:

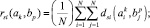
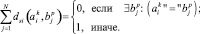
Таким образом, мера близости двух уровней в МТП A и B определяется количеством совпавших (по наименованиям) операций.

Для нахождения минимального расстояния rsi между МТП A и B по шкале наименований можно применить подход к сравнению уровней иерархий, описанный в работе [1], основанный на методе динамического программирования. При известных значениях расстояний между отдельными уровнями, записанными в общую матрицу, он сводится к поиску минимального пути из верхнего левого угла матрицы в нижний правый угол. Значение некоторой функции качества r(i, j) принимается на следующем шаге равным

r(i, j) + min(r(i, j + 1), r(i + 1, j), r(i + 1, j + 1)),

причем движение по горизонтали и вертикали в некоторых случаях «штрафуется» весовым коэффициентом. Заметим, что этот общий принцип нахождения расстояний положен в основу вычисления всех последующих расстояний независимо от выбранной шкалы.

Введем расстояние между двумя МТП с учетом особенностей этапов их выполнения по шкале времени (time scale). Для сравнения по этому принципу можно применить метод DTW, подробно рассмотренный автором в работе [8]. Такой подход позволяет найти минимальное расстояние rst между двумя МТП без конкретизации каждого уровня. Алгоритм DTW вычисляет оптимальную последовательность трансформации (деформации) времени между двумя временными рядами [10]. Пусть заданы две числовые последовательности (a1, a2, ..., an), (b1, b2, ..., bm). Получим матрицу D отклонений, в которой

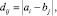i = 1, ..., n; j = 1, ..., m.

На втором этапе строим матрицу деформаций, каждый элемент которой rij определяется при помощи алгоритма динамического программирования и критерия локальной оптимизации:

rij = dij + min(ai–1,j–1, ai–1,j, ai,j–1).

Путь деформации начинается в левом верхнем углу и заканчивается в правом нижнем. Величина деформации rst определяется суммой минимальных локальных отклонений, нормируется путем деления на количество элементов пути и служит оценкой расстояния между последовательностями.

Для получения общей меры сравнения двух МТП в случае применения двух шкал различного типа можно воспользоваться евклидовым расстоянием

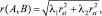
или аддитивной сверткой

r(A, B) = λ₁rsi + λ₂rst,

где λ₁, λ₂ – весовые коэффициенты, определяющие важность составных частей расстояния, причем λ₁ + λ₂ = 1. Рассмотрим, в качестве примера далее подходы к выбору значений коэффициентов для аддитивной свертки.

Выбор весовых коэффициентов в аддитивных мерах расстояний

Для установления весов привлекаются эксперты, которые оценивают важность каждого критерия. Представляют интерес два метода рейтинговой оценки критериев качества с помощью экспертов [7, 9]: метод ранжирования и метод парных сравнений.

Рассмотрим вначале метод ранжирования. Пусть имеются m экспертов, которые оценивают n критериев. Каждый эксперт проводит ранжирование критериев путем присваивания номеров от 1 до n в соответствии с убыванием степени важности этих критериев, при этом заполняется таблица (табл. 2).

Таблица 2

Ранжирование экспертами критериев качества

Здесь xij – номер, который i-й эксперт присвоил j-му критерию. В дальнейшем удобно пересчитать эту таблицу, присваивая более важному критерию большее число yij (i = 1, 2, ..., m; j = 1, 2, ..., n). Введем новые веса yij = n – xij. Теперь наиболее важный критерий имеет оценку n – 1, а наименее важный – нуль. Весовые коэффициенты в аддитивном критерии определяются таким образом:

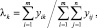k = 1, 2, ..., n.

Степень согласия работы экспертов определяется коэффициентом:

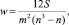
где

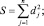
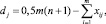
j = 1, 2, ..., n.

Значения w изменяются в пределах w ∈ [0; 1]. Если w = 1, то все эксперты дают одинаковые оценки, если w = 0, то мнения экспертов несогласованные. В зависимости от величины коэффициента w результаты оценки критериев либо принимаются, либо отвергаются. В последнем случае следует сменить состав экспертов и повторить эксперимент. Рассмотрим метод парных сравнений, который применяется в случае, когда эксперты затрудняются в оценке важности критериев в баллах. В этом случае каждый k-й эксперт заполняет следующую таблицу (табл. 3).

Таблица 3

Сравнение критериев качества

Здесь 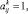(i = 1, 2, ..., n; j = 1, 2, ..., n; k = 1, 2, ..., m, если i-й критерий предпочтительнее j-го критерия, 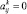, в противном случае.

Таким образом, получают всего m таблиц. Далее происходит объединение таблиц в одну путем суммирования чисел, стоящих в соответствующих клетках:

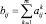
Определим весовые коэффициенты:

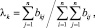(k = 1, 2, ..., n).

Степень согласованности экспертов:

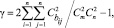
где 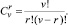Максимальное значение коэффициента согласия γ_max = 1. Минимальное значение: 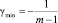для m – четного и 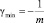– для m нечетного.

Пример построения метрики

Рассмотрим пример применения предложенного подхода для сравнения процессов лечения заболевания бронхиальной астмой, приведенных в табл. 4 (данные представлены Медицинским центром ЦБ РФ). Таблица содержит шаблон процесса лечения пациентов в соответствии со стандартом, который определяет обязательные для выполнения операции и отчеты выполнения реальных процессов лечения трех пациентов.

Таблица 4

Процессы лечения бронхиальной астмы

Таблица 5

Отклонение процессов лечения (шкала наименований)

Таблица 6

Отклонение процессов лечения (шкала времени)

Таблица 7

Отклонение процессов лечения (обобщенное расстояние)

Результаты парного сравнения процессов лечения всех пациентов с применением шкалы наименований приведены в табл. 5.

Результаты парного сравнения процессов лечения всех пациентов с применением шкалы времени приведены в табл. 6.

Используя аддитивную свертку, вычислим общие расстояния между МТП (табл. 7).

Табл. 5–7 демонстрируют возможность измерения отклонений различных процессов лечения от стандарта и между собой, что представляет интерес для лечащих врачей.

Заключение

В статье рассмотрен метод измерения расстояний между двумя иерархическими структурами, который предполагается применить для сравнения различных вариантов медицинских технологических процессов. Метод основан на обобщении расстояний по двум шкалам, учитывающим возможности отклонений по времени и составу выполнения медицинских мероприятий при лечении пациентов одной нозологии. Полностью отойти от субъективной оценки хода лечения в связи с учетом мнения экспертов при определении важности критериев и без знаний исходов лечения не представляется возможным. Тем не менее предполагается, что такой подход позволит лечащему врачу проводить детальный анализ прецедентов лечебного процесса, следить за собственным ходом выполнения обязанностей, избегая грубых отклонений от рекомендаций, и накапливать знания в предметной области.

Работа выполнена при финансовой поддержке проектов РФФИ № 16-29-12839 офи-м «Разработка моделей, методов и инструментальных средств для синтеза оптимизированных технологических цепочек и технологических процессов на основе интегрированных баз знаний и интеллектуальных технологий автоматической генерации и оценки планов», 16-37-00034 мол_а «Исследование и разработка методов анализа отклонений выполненных медицинских технологических процессов от их типовой схемы».

Библиографическая ссылка