Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ланкин А.М. 1

---

1 ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова»

В статье описано применение одного из проекционных методов – метода главных компонент к динамическим характеристикам намагничивания. Метод главных компонент позволяет выявить латентные признаки и одновременно уменьшить размерность исходных данных, пожертвовав малозначимой информацией. С помощью приведенного подхода динамическая характеристика намагничивания преобразуется в точку в пространстве главных компонент, что позволяет ограничиться только значимой информацией и исключить случайные помехи и случайные составляющие погрешности измерений. Рассмотрены полученные экспериментальные результаты по применению метода главных компонент к динамическим характеристикам намагничивания пропорциональных электромагнитов с различными отклонениями, возникшими в ходе их технологического процесса производства. Для исследуемых динамических характеристик намагничивания первые две компоненты позволили описать более 99?% общей дисперсии.

Статья в формате PDF

0 KB

динамическая характеристика намагничивания

проекционные методы

метод главных компонент

1. Антонов В.Г., Петров Л.М., Щелкин А.П. Средства измерений магнитных параметров материалов. – Л.: Энергоатомиздат, 1986. – 216 с.

2. Болч Б., Хуань К.Д. Многомерные статистические методы для экономики – М.: Статистика, 1979. – 317 с.

3. Гордон А.В., Сливинская А.Г. Электромагниты постоянного тока – М.: Государственное энергетическое издательство, 1960. – 447с.

4. Сливинская А.Г. Электромагниты и постоянные магниты. – М.: Энергия, 1972, – 248 с.

5. Ковалев О.Ф. Комбинированные методы моделирования магнитных полей в электромагнитных устройствах. – Ростов н/Д.: Изд-во СКНЦ ВШ, 2001. – 220 с.

6. Эсбенсен К. Анализ многомерных данных. Избранные главы: пер. с англ. С.В. Кучерявского; под ред. О.Е. Родионовой. – Барнаул: Изд-во Алт. ун-та, 2003. 157 с.

Как известно, динамическая характеристика намагничивания (ДХН) пропорционального электромагнита содержит латентную информацию о большинстве его параметров [3, 4, 5], однако она имеет сложный, неоднозначный характер, что затрудняет ее анализ, с целью выявления информации, требуемой для выработки управляющих технологическим процессом сигналов. Поэтому необходимо снижать размерность анализируемой информации с помощью проекционных подходов.

Для снижения размерности анализируемой информации в настоящее время находит применение проекционный подход, использующий метод главных компонент (ГК), для снижения размерности анализируемой информации [1]. Сущность метода главных компонент состоит в переходе от исходных переменных к новым величинам – главным компонентам, которые представляют собой линейные комбинации исходных переменных [2]. При этом первая главная компонента описывает максимальную дисперсию и является нормированной линейной комбинацией всех возможных исходных признаков, а вторая – учитывает максимальное значение оставшейся дисперсии и корреляционно не связана с первой компонентой и так далее до n (n – количество ГК). Обычно учитываются только (n – l) наибольших ГК, сумма значимостей которых лежит в пределах 0,8–0,99 (l – количество незначимых ГК).

Рассмотрим применение метода главных компонент к группе содержащей k ДХН пропорциональных электромагнитных приводов. Координаты точек i(Ф) в силу зависимости их от многих технологических режимов и неучитываемых случайных помех, а также наличия случайной составляющей погрешности измерения можно считать случайными величинами. Исходя из этого, координаты точек каждой ДХН будем рассматривать как вектор.

На исходной кривой выберем n фиксированных значений магнитного потока

Фd = d•ΔФ;

ΔФ = Фmax/n,

где Фmax – максимально возможное значение потока для всех исследуемых характеристик; n – выбранное количество фиксированных значений потока; d – номер точки.

Определяются значения токов i1(Фd), которые и являются элементами формируемого вектора I1.

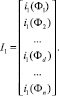
Аналогично формируются векторы для других ДХН, причём значения токов i определяются для тех же фиксированных значений магнитного потока Фd.

Здесь хотелось бы отметить, что применение кусочной аппроксимации к ДХН позволяет вычислить путем интерполяции недостающие значения векторов ij(Фd), в случае если Фjmax меньше, чем Фmax.

Полученные таким образом векторы записываются в одну матрицу I размерности n×k, где n – количество фиксируемых точек, а k – число исследуемых кривых:

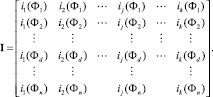
Для нахождения ковариации определим вектор выборочных средних по строкам 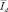. Следующим шагом определим отклонения от среднего для каждого наблюдения и сведём эти отклонения в матрицу F, каждый элемент которой формируется по следующей формуле:

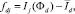d = 1...n, j = 1...k.

Поскольку значение числа наблюдений n ограничено, то можно найти лишь оценку ковариации S:

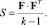
Найдём вектор характеристических чисел L и матрицу характеристических векторов B матрицы S:

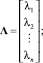
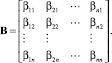
Используя полученные матрицы, найдём ГК. Размерность пространства, в котором распределены точки матрицы I, равна числу строк этой матрицы, т.е. n, тогда

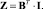
Размерность получаемой матрицы такая же, как и у матрицы I:

Полученные таким образом ГК упорядочиваются в соответствии со значимостью, т.е. по возрастанию соответствующих собственных чисел.

Как указывалось выше, не все ГК являются значимыми, поэтому отбросим незначимые l ГК, оставив только (n – l) компонент. При правильном определении числа l оставшиеся главные компоненты несут в себе всю необходимую информацию об исходном распределении. В то время как отброшенные ГК содержат в себе информацию о случайной помехе или шуме. Отбрасывание l главных компонент означает, что размерность пространства, в которое проецируются точки исходного распределения, сокращается, т.е. сокращается число базисных векторов пространства ГК. Поскольку в рассматриваемом пространстве в качестве базисных векторов выступают характеристические векторы матрицы S, то вместе с уменьшением числа ГК необходимо уменьшить и число характеристических векторов. Таким образом, после описанных преобразований матриц Z и B имеем следующий вид:

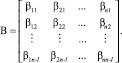
Суммарная размерность получившихся матриц при достаточно большом l будет меньше размерности исходной матрицы I.

Таким образом, по результатам этого шага мы получаем новое пространство главных компонент, каждая точка которого представляет собой ДХН конкретного изделия.

В качестве примера спроецируем ДХН1 – ДХН9 с различными технологическими отклонениями в пространство ГК. Вначале сформируем исходную матрицу токов I. Для этого для каждой ДХН используем следующий подход: задавшись максимальным значением Фmax = 0,17 Вб и количеством фиксируемых точек n = 35, определяем DФ = 0,005 и определяем значения токов ij(Фd).

На рис. 1 представлены ДХН1-ДХН9, а в табл. 1 соответствующие им отклонения параметров. Табл. 2 содержит значения токов матрицы I для ДХН1-ДХН9, а табл. 3 – соответствующие значения вычисленных ГК Z. Существует верхний предел количества возможных ГК, который для центрированных величин равен k, а для нецентрированных k – 1, однако количество ГК не может быть больше n [6]. Таким образом, максимально возможное количество ГК для проводимого эксперимента девять.

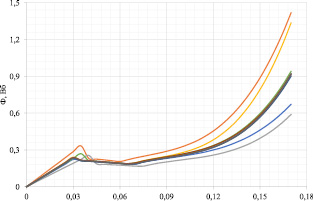
Рис. 1. ДХН пропорциональных электромагнитов с технологическими отступлениями от номинала

Таблица 1

Типы дефектов в исследуемых пропорциональных электромагнитах

Таблица 2

Значения магнитного потока и токов ДХН1–ДХН9

Таблица 3

Значения ГК для ДХН1–ДХН9

Рис. 2. Проекции измеренных ДХН в пространство ГК

В табл. 4 приведены значения описанной дисперсии для разного количества использованных ГК. Из таблицы видно, что достаточно использовать всего две ГК, описывающие более 95 % всей дисперсии, а дальнейшее увеличение их количества практически не повышает описываемую дисперсию.

Таблица 4

Зависимость описанной дисперсии от количества использованных ГК

На рис. 2 показано пространство главных компонент Z1 и Z2, где каждая точка является проекцией одной из исходных ДХН.

Таким образом, применение проекционного подхода позволяет снижать размерность анализируемой измерительной информации, при этом сохраняя значимую составляющую данных и отбрасывая случайные помехи и возможные случайные составляющие погрешности измерений.

Результаты работы получены при поддержке проекта № 1.2690.2014/K «Методы решения обратных задач диагностики сложных систем (в технике и медицине) на основе натурно-модельного эксперимента», выполняемого в рамках проектной части государственного задания с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ (НПИ).

Библиографическая ссылка