Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Артемов М.А. 1 Барановский Е.С. 1 Потапов Н.С. 1

---

1 ФГБОУ ВО «Воронежский государственный университет»

Рассматриваются математические модели жесткопластического и упругопластического тела. Проводится сравнение форм записи условия пластичности Мизеса и Треска для плоского деформированного состояния жесткопластического тела. Обсуждается, когда для условия пластичности Треска в рамках теории пластического течения существует решение задачи об осесимметричном плоско-деформированном состоянии при выполнении режима полной пластичности для жесткопластического тела. Используется корректная форма записи режимов пластичности для кусочно-линейных условий пластичности общего вида. Для модели, учитывающей упругую и пластическую сжимаемость, при выборе кусочно-линейного условия пластичности общего вида предложен алгоритм, позволяющий определять условия, при выполнении которых на границе осесимметричной цилиндрической области зарождается пластическая зона, соответствующая выбранному режиму пластичности. Получены формулы для определения напряжений и деформаций для некоторых режимов пластичности, когда в пластической зоне реализуются один и два режима пластичности.

Статья в формате PDF

0 KB

математическое моделирование

упругопластическое тело

жесткопластическое тело

плоская деформация

кусочно-линейные условия пластичности

теория пластического течения

1. Артемов М.А., Барановский Е.С. Математическое моделирование пластического состояния тел. Плоская деформация // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. – 2015. – № 2 (24). – С. 72–87.

2. Артемов М.А., Барановский Е.С., Якубенко А.П. Альтернативные формы записи кусочно-линейных условий пластичности и их обобщения // Вестник Воронежского государственного университета. Серия: Физика. Математика. – 2015. – № 1. – С. 71–82.

3. Артемов М.А., Бестужева Н.П., Потапов Н.С. О выполнении условия полной пластичности при плоском деформированном состоянии // Вестник Воронежского государственного технического университета. – 2010. – Т. 6, № 7. – С. 88–92.

4. Артемов М.А., Ивлев Д.Д. Об общих соотношениях теории идеальной пластичности при кусочно-линейных условиях текучести // Доклады Академии наук. – 1996. – Т. 350, № 3. – С. 332–334.

5. Артемов М.А., Ларин И.А. Учет сжимаемости материала при определении напряженно-деформированного состояния в упругопластическом теле в случае плоской деформации // Вестник Воронежского государственного технического университета. – 2009. – Т. 5, № 7. – С. 39–42.

6. Артемов М.А., Потапов Н.С., Якубенко А.П. Математическое моделирование равновесного состояния круговой цилиндрической трубы // Вестник Воронежского государственного технического университета. – 2011. – Т. 7, № 5. – С. 126–128.

7. Артемов М.А., Потапов Н.С., Якубенко А.П. О соотношениях, вытекающих из условия пластичности Треска // Вестник Воронежского государственного технического университета. – 2011. – Т. 7, № 3. – 2011. – С. 7–8.

8. Артемов М.А., Потапов Н.С., Якубенко А.П. Условие полной пластичности и ассоциированный закон деформирования // Вестник Воронежского государственного технического университета. – 2009. – Т. 5, № 9. – С. 18–23.

9. Артемов М.А., Потапов Н.С., Якубенко А.П. Следствия нормального закона пластического течения // Вестник Воронежского государственного технического университета. – 2009. – Т. 5, № 9. – С. 145–147.

10. Артемов М.А., Якубенко А.П. К задаче Ламе // Теоретические и прикладные вопросы образования и науки: сборник научных трудов по материалам Международной научно-практической конференции. Часть 9. – Тамбов, 2014. – С. 11–12.

11. Соколовский В.В. Теория пластичности. – М.: Высшая школа, 1969. – 608 с.

12. Gamer U. On the Elastic-plastic Shrink Fit with Supercritical Interference // Acta Mechanica. – 1986. – Vol. 61. – P. 1–14.

Вопросам математического моделирования объектов, проявляющих упругопластические свойства, посвящено большое количество работ. Однако некоторые известные математические модели и алгоритмы решения задач ставят ряд вопросов. Так, осесимметричная задача для плоского деформированного состояния для сжимаемого упругопластического тела вызывает постоянный интерес и ряд дискуссий [12], обусловленных поиском правильного решения при рассмотрении кусочно-линейных условий пластичности. В работах [1, 2] обсуждались альтернативные формы записи кусочно-линейных условий пластичности. Общие соотношения при выполнении условия полной пластичности приведены в [8]. Решение конкретных задач при учете упругой и пластической сжимаемости для кусочно-линейных условий пластичности даны в [3, 5, 6]. В работе [4] обсуждалась статическая и кинематическая определимость для пластического тела. Ошибки, связанные с некорректной формой записи кусочно-линейных условий пластичности, обсуждались в [2, 7].

Модели жесткопластического тела

Для плоского деформированного состояния при выборе математической модели изотропного жесткопластического тела, когда пластический потенциал является четной функцией тензора напряжений, осевое напряжение σ_z является средним арифметическим двух других главных напряжений. Если функция пластичности и пластический потенциал совпадают, то для условия пластичности Треска осевое напряжение остается неопределенным [9]

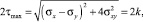
σ_min ≤ σ_z ≤ σ_max.

При этом задача плоской деформации будет локально статически определимой для компонент тензора напряжений σ_x, σ_y, σ_xy. Если выбирается условие пластичности Треска, то определение всех компонент тензора напряжений при плоской деформации возможно, когда вводится некоторое дополнительное предположение. Так, для осесимметричного состояния при выборе режима полной пластичности

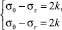(1)

в области a ≤ r ≤ b, на границе которой задано давление 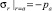, имеет место

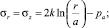σ_θ = 2k + σ_r.

Здесь (r, θ, z) – цилиндрической системы координат.

Если, например, выбирается условие пластичности Мизеса, то в случае плоской деформации имеем [11]

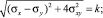
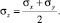
Однако задача не является статически определимой, поскольку равенство 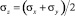является следствием определяющих уравнений, включающих кинематические величины.

Ниже рассматривается плоское деформированное состояние, когда выбирается модель упругопластического тела.

Модель упругопластического тела

Для сжимаемого упругого тела в задаче Ламе осевое напряжение не всегда может быть средним [3]. Такая же особенность может иметь место и для упругопластического тела. Для упругого состояния цилиндрической области a ≤ r ≤ b, нагружаемой внешним давлением pb и внутренним давлением pa [11],

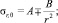
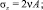
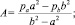
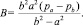(2)

Все функции пластичности вида 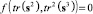(s – девиатор напряжений), для напряженного состояния (2) принимают наибольшее значение на границе r = a, поэтому пластическая зона будет зарождаться на этой границе.

Рассмотрим i-й режим кусочно-линейного условия пластичности общего вида (корректная форма записи для кусочно-линейного условия пластичности)

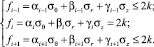(3)

Условия, при выполнении которых на границе r = a при зарождении пластической зоны будет выполняться режим (3), определяются по следующему алгоритму: в соотношениях (3) компоненты напряжений заменяются с учетом формул (2) и r = a. Далее, используя неравенства f _i–1 ≤ k и f _i+1 ≤ k, находятся допустимые границы изменения одного из давлений: pa или pb. Реализуя указанный алгоритм, приходим к следующим формулам:

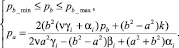
Величины pb_max и pb_min являются наибольшим и наименьшим значениями pb, определяемым из равенств

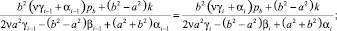
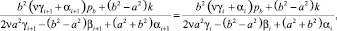
которые получаются из равенств fi = fi–1, fi = fi+1 после подстановки в них (2).

Аналогично определяется диапазон допустимых значений давлений для pa (p _{a_min} ≤ p_a ≤ p _{a_max}). Значения pa_max и pa_min определяются как наибольшее и наименьшее из следующих выражений:

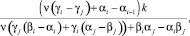
когда j = i – 1 и j = i + 1. В этом случае давление на внешней границе

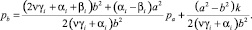
Для кусочно-линейных условий пластичности частного вида эти формулы были получены ранее в [10].

Пример реализации алгоритма определения режима пластичности

Наиболее известное решение задачи об определении напряженного и деформированного состояния для осесимметричной цилиндрической трубы a ≤ r ≤ b, на боковых границах которой заданы давления pa, pb или перемещения ua, ub, относится к режиму пластичности Треска

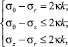(4)

где k = const; κ = sign(σ_θ – σ_r). Из уравнения равновесия

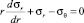
и системы (4), когда σ_r(r = a) = –p_a, решая начальную задачу, находим окружное и радиальное напряжения:

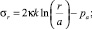
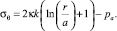(5)

Из ассоциированного с условием (4) закона пластического течения, принимая гипотезу о естественном состоянии, следуют пропорции

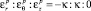
для пластических деформаций. Поскольку для осевой деформации

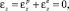
то из закона Гука, учитывая формулы (5), находим, что

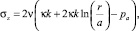(6)

где ν – коэффициент Пуассона.

Из закона Гука, учитывая формулы (5), (6), определяем упругие деформации в пластической зоне

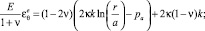
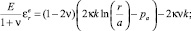
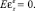(7)

Полные деформации определяются суммой упругих и пластических деформаций. Поэтому из соотношений ассоциированного закона пластического течения, с учетом связи полых деформаций и перемещений, следует уравнение для радиальной компоненты вектора перемещений

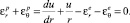(8)

Учитывая формулы (7) и решая уравнение (8), находим перемещения и полные деформации в пластической зоне:

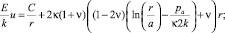
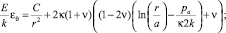
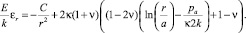(9)

Пластические деформации равны разности полных и упругих деформаций

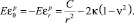(10)

Из того, что на упругопластической границе r = C пластические деформации равны нулю, следует равенство C = 2κ(1 – ν²)c².

Применяя предложенный выше алгоритм, находим, что режим (4) может зарождаться на границе r = a, если

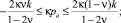
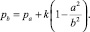
Выполнение одного режима пластичности

Решение (5)–(7), (9), (10) справедливо в области a ≤ r ≤ c пластического состояния, если радиус упругопластической границы

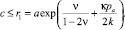
Граница r1 находится из условия σ_r = σ_z. На границе r = r1 для напряжений имеет место равенство

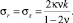
Из этой формулы видно, что безразмерное радиальное напряжение σ_r/k зависит только от значения коэффициента Пуассона и всегда будет положительным (растягивающие усилия).

Если c ≤ r1, то в пластической зоне реализуется только режим (4), когда

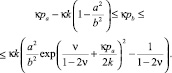
Радиус упругопластической границы определяется из уравнения

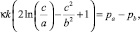
которое для выбранного алгоритма решения задачи, учитывая (5), находится из граничного условия 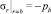. Для режима (4) из формул (5), (6) следует, что для радиуса упругопластической границы условие a ≤ c = r₁ ≤ b выполняется, если

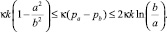
В упругой зоне c ≤ r ≤ b коэффициенты A, B, входящие в формулы (2), можно найти, используя условие непрерывности напряжений на границе r = c. Так что в области c ≤ r ≤ b

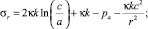
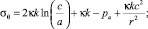
σ_r = ν(σ_r + σ_θ).

Выполнение двух режимов пластичности

Из формул (5), (6) при r > r1 следует, что 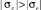, поэтому в области пластического состояния a ≤ r ≤ c (r1 ≤ c) на границе r = r1 произойдет переход к режиму пластичности

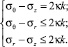(11)

Для этого режима задача статически неопределима. Поэтому определение напряженного состояния требует совместного рассмотрения всех уравнений (основных и определяющих).

Для режима (11) напряжения определяются по формулам [6]

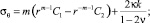
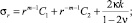
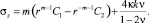(12)

Из условия непрерывности напряжений на границе r = r1 из формул (5) и (12) находим

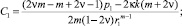
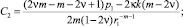
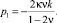
Если радиус упругопластической границы r1 < c, то в пластической зоне реализуются два режима: (4) и (11). В этом случае в упругой зоне c ≤ r ≤ b

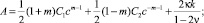
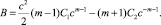
Радиус упругопластической границы, как и раньше, находится из граничного условия

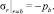
Поскольку сингулярные режимы пластичности для рассматриваемой задачи не реализуются [1], то при переходе от одного режима пластичности (3) к другому соотношения ассоциированного закона пластического течения приводят к разрыву компонент пластических деформаций, что указывает на необходимость указания границ применения математических моделей подобного типа.

Выводы

Для сжимаемого упругопластического тела предложен алгоритм, позволяющий определять диапазоны изменения давлений на стенках круговой трубы, когда переход в пластическое состояние выполняется для любого режима кусочно-линейного условия пластичности. Для жесткопластического тела решение осесимметричной задачи плоской деформации возможно для некоторых режимов кусочно-линейного условия пластичности. При выборе условия пластичности Треска для трубы, находящейся в предельном состоянии, может существовать область, в которой выполняется условие полной пластичности. Предложенный алгоритм определения режима кусочно-линейного условия пластичности позволяет получать корректные решения для осесимметричной задачи плоской деформации.

Библиографическая ссылка