В последние годы заметно снизился диаметр пиловочника и все шире в практике лесопиления и деревянного домостроения стало использоваться тонкомерное сырье. Это отразилось не только на размерных характеристиках пиломатериалов, но и на качественных. При сушке пиломатериалов, полученных при распиловке тонкомера, заметно возросли потери сухой древесины из-за различного вида коробления и других дефектов. Значительное влияние, на наш взгляд, на качество сушки оказывают начальные напряжения, сформировавшиеся в стволе дерева в процессе его роста.
Проблеме повышения качества пиломатериалов, получаемых из тонкомерного сырья, посвящено значительное число работ проф. В.И. Мелехова [1–5], В.Е. Бызова и др.
В процессе роста дерева в его стволе развиваются и формируются начальные напряжения под действием собственного веса кроны, осадков и в значительной мере – ветровой нагрузки.
В ответ на образование напряженно-деформированного состояния от внешних воздействий и соответствующего развития клеток древесины формируется напряженно-деформированное состояние ствола дерева. По данным А.И. Кузнецова [6], максимальные напряжения в стволе достигают предельных значений независимо от значения критической скорости ветра для каждой местности. В соответствии с ветровой нагрузкой формируется ствол дерева, в том числе и его сбег, как стержень равного сопротивления.
По величине относительного размера ядра и заболони можно судить о характере распределения начальных напряжений по радиусу сечения ствола, от чего зависит формирующаяся прочность древесины при растяжении и сжатии вдоль волокон и при изгибе.
Известны две основные гипотезы, объясняющие образование и развитие начальных напряжений. Одна предполагает, что механические напряжения от внешних воздействий являются стимулятором притока питательных веществ в наиболее напряженные части ствола дерева. Клетки древесины увеличивают свое сопротивление растяжению (сжатию) за счет увеличения толщины стенок. Другая гипотеза предполагает появление начальных напряжений из-за наклона фибрилл в стенках древесных клеток, в результате чего волокна приобретают спиралевидную форму. С увеличением влажности наклон фибрилл нарастает и продольный размер клетки уменьшается, а поперечный увеличивается. Этим объясняется появление напряжений растяжения в заболонной и сжатия в ядровой зонах ствола.
В процессе сушки в пиломатериалах должен происходить обратный процесс. При снижении влажности должно появляться продольное коробление, обратное тому, которое наблюдается в практике. При снижении влажности пиломатериалов угол наклона микрофибрилл уменьшается, длина клеток увеличивается и постепенно начальные напряжения уменьшаются. Если учитывать только этот физико-химический фактор, то при выравнивании влажности по сечению пиломатериалов начальные напряжения должны исчезнуть полностью. Однако на практике этого не происходит. Подтверждением этому служит продольная покоробленность высушенных досок, по причине которой до 25–40 % объема высушенных пиломатериалов понижает свою сортность. Поэтому, по нашему мнению, главенствующую роль в образовании все-таки играет механический фактор, не исключая при этом влияния физико-химического фактора.
На основании предположений, подтвержденных результатами исследований А.И. Кузнецова [6], H. Kubler [7], A. Julinen [8], периферийная (заболонная) зона в продольном направлении растянута, а ядровая сжата.
Принимая функцию начального напряжения в виде параболоида 2-го порядка (рис. 1), можно определить размер ядровой зоны:
σн = k(y2 + z2) – σ0, (1)
где 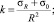 σR, σ0 – значения начального напряжения в направлении вдоль волокон древесины в точках на контуре и в центре сечения соответственно; из уравнения равновесия σR = σ0; R – радиус сечения ствола; R0 – радиус ядровой зоны, определяемый из (1):
σR, σ0 – значения начального напряжения в направлении вдоль волокон древесины в точках на контуре и в центре сечения соответственно; из уравнения равновесия σR = σ0; R – радиус сечения ствола; R0 – радиус ядровой зоны, определяемый из (1):
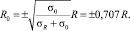 (2)
(2)
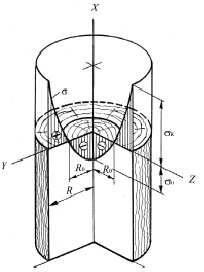
Рис. 1. Эпюра начальных напряжений в стволе дерева в направлении вдоль волокон
Другому размеру ядра сечения будет соответствовать более сложная функция распределения начального напряжения по радиусу сечения.
При ветровой нагрузке к начальным напряжениям добавятся напряжения изгиба ствола, и суммарное напряжение будет таким:
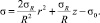 (3)
(3)
Для точек сечения, расположенных в плоскости действия ветровой нагрузки, напряжение можно вычислить по формуле
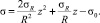 (4)
(4)
Полученная функция (4) при исследовании ее на экстремум принимает максимальное значение в зоне сжатия:
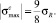 (5)
(5)
Максимальное напряжение в растянутой зоне при использовании формулы (4):
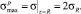 (6)
(6)
В точках на контуре сечения напряжение растяжения в 2 раза больше напряжения в центре. Учитывая характер изменения суммарного напряжения по радиусу сечения, можно предположить, что максимальное напряжение в точке на контуре в зоне растяжения достигает предела прочности при изгибе, а в зоне сжатия – предел прочности при сжатии вдоль волокон. Их отношение при распределении начальных напряжений по закону параболоида 2-й степени составляет
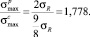 (7)
(7)
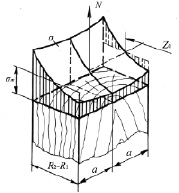
Рис. 2. Распределение начальных напряжений вдоль волокон доски до выпиловки ее из бревна
Равнодействующую начальных напряжений в пиломатериалах в рассматриваемом случае находим решением следующего интеграла (рис. 2):
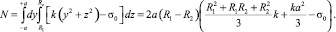 (8)
(8)
Средняя величина начального напряжения в сечении:
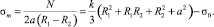 (9)
(9)
Используя (9) и (1), можно определить величину изгибающего момента от усилий, выходящих на торец доски и изгибающих ее по пласти:
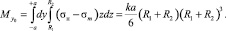 (10)
(10)
Значения 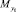 на каждом торце доски будут различными по величине в соответствии со значениями R, R1, R2, a.
на каждом торце доски будут различными по величине в соответствии со значениями R, R1, R2, a.
Начальные напряжения могут способствовать увеличению прогиба доски от действия ее собственного веса, а могут и препятствовать появлению изгиба (рис. 3).
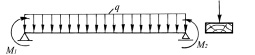
а
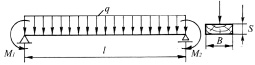
б
Рис. 3. Схема нагружения доски собственным весом моментами от начальных напряжений, выходящих на торцы: а – при верхнем расположении наружной пласти; б – при нижнем расположении наружной пласти
Используя принцип независимости действия сил, можно разделить влияние собственного веса доски и начальных напряжений на деформацию изгиба. Появляется возможность по прогибу доски со стороны одной и другой пластей оценить ее прочность при изгибе и отдельно определить величину начальных напряжений.
По результатам измерения прогибов доски со стороны наружной и внутренней пластей (рис. 3) можно вычислить величину начальных напряжений и модуля упругости при изгибе и по нему установить класс прочности пиломатериалов.
Управление прогибов доски в верхнем положении пласти (рис. 3, а) имеет такой вид:
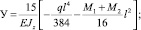 (11)
(11)
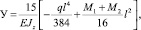 (12)
(12)
где E – модуль упругости древесины при изгибе, МПа [9]; 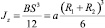 – осевой момент инерции доски, мм4; q – интенсивность распределения собственного веса доски по ее длине; q = 2a(R1 + R2)γ; γ – объемный вес древесины при соответствующей влажности доски [10]; M1, M2 – моменты на торцах доски от действия начальных напряжений, Н•мм; l – длина доски, м.
– осевой момент инерции доски, мм4; q – интенсивность распределения собственного веса доски по ее длине; q = 2a(R1 + R2)γ; γ – объемный вес древесины при соответствующей влажности доски [10]; M1, M2 – моменты на торцах доски от действия начальных напряжений, Н•мм; l – длина доски, м.
В таблице приведены результаты расчетов прогибов пиломатериалов после распиловки бревен при следующих данных (рис. 4).
Ниже приведено решение задачи по определению прогиба пиломатериалов, получаемых при распиловке тонкомерного бревна с диаметром вершинного торца 12 см. Прогиб от действия начальных напряжений значительно превышает прогиб от действия собственного веса пиломатериалов. При этом напряжение изгиба составляет третью часть от предела прочности древесины при статическом изгибе. Расчет показывает, что укладывать такие пиломатериалы в верхние 3–5 рядов сушильного штабеля нецелесообразно из-за продольного коробления по пласти и по кромке.
В примере можно видеть, что при появлении смещения сердцевины относительно геометрического центра сечения начинает увеличиваться продольное коробление (таблица).
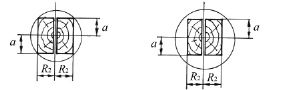
а
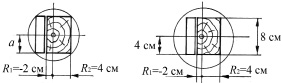
б
Рис. 4. Схема распиловки тонкомерного сырья: а – на две доски без сердцевины; б – на брус с сердцевиной и доску
Начальные напряжения и прогиб сосновых пиломатериалов при следующих данных: W = 40 %; l = 4 м; E = 8900 МПа
|
Радиус сечения бревна R, см |
k1 |
k2 |
R1, см |
R2, см |
a, см |
ум |
уq |
|
|
– в верхнем торце 6 |
1,047·10–2 |
0,465·10–2 |
0 |
4 |
4 |
6,8 |
1,614 |
7,78 |
|
6 |
1,047·10–2 |
0,465·10–2 |
1,5 |
4 |
4 |
9,345 |
4,1354 |
7,958 |
|
6 |
1,047·10–2 |
0,465·10–2 |
–2 |
4 |
4 |
4,893 |
0,718 |
5,69 |
|
6 |
1,047·10–2 |
0,465·10–2 |
–1 |
4 |
4 |
5,097 |
1,489 |
5,67 |
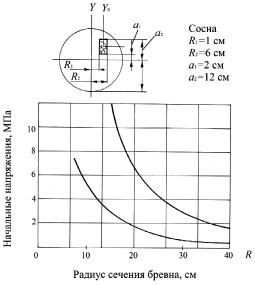
Рис. 5. Влияние радиуса сечения ствола на величину начальных напряжений при изгибе по пласти и по кромке: 1 – при изгибе по кромке; 2 – при изгибе по пласти
На рис. 5 проиллюстрировано влияние диаметра пиловочника на величину изгибающего момента по пласти и по кромке от действия начальных напряжений. С уменьшением диаметра бревен следует ожидать получение пиломатериалов, качество последующей сушки которых прогнозируется невысоким из-за чрезмерного продольного пластевого и кромочного коробления. Для уменьшения потерь из-за дефектов сушки необходимо использовать дополнительные прижимные устройства для оснащения ими сушильных штабелей.
При выпиливании квадратных брусков потребуется более тщательное базирование бревен, чтобы центр сердцевины совпадал с геометрическим центром бруска (рис. 4).
Приведенная методика позволяет вычислить величину начального напряжения в пиломатериалах по величине прогибов доски со стороны ее наружной и внутренней пластей с использованием опытных значений модуля упругости древесины при изгибе. Для этого необходимо представить прогиб доски в виде суммы ее прогибов от действия собственного веса и от действия начальных напряжений (рис. 3), когда направление их совпадает:
y1 = yq + yм. (13)
И в виде разности прогибов от собственного веса и от действия начальных напряжений, когда направления их противоположны:
y2 = yq + yм. (14)
Тогда полусумма двух измерений (13) и (14) будет характеризовать прогиб доски от действия только ее собственного веса:
y1 + y2 = yq + yм + yq – yм = 2yq,
т.е.
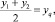 (15)
(15)
а полуразность двух измерений будет характеризовать прогиб от действия начальных напряжений:
y1 – y2 = yq + yм – yq + yм = 2yм;
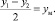 (16)
(16)
С другой стороны, прогиб в середине пролета можно вычислить по формуле
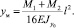 (17)
(17)
Приравнивая левые и правые части (17) и (16), получим формулу, связывающую модуль упругости доски при изгибе с ее прогибами со стороны обеих пластей и моментами от начальных напряжений:
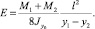 (18)
(18)
Последнюю формулу можно применить для определения моментов от действия начальных напряжений при известном модуле упругости:
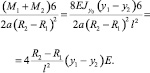 (19)
(19)
Выводы:
– впервые разработана методика определения начальных напряжений в пиломатериалах, сформировавшихся в стволах деревьев в процессе их роста;
– с уменьшением диаметра ствола возрастает начальное напряжение в пиломатериалах и величина продольного коробления;
– пиломатериалы, выпиленные из тонкомерного сырья, в процессе последующей сушки должны быть уложены в сушильном штабеле с механическим прижимом;
– при сушке без прижима в 3–5 верхних рядах штабеля значительная часть досок будет иметь чрезмерное коробление;
– измерение прогиба досок со стороны наружной и внутренней пластей позволяет объективно оценить и величину начальных напряжений, и прочность пиломатериалов при изгибе.
Библиографическая ссылка
Акопян А.Л. ПРОДОЛЬНОЕ КОРОБЛЕНИЕ ПИЛОМАТЕРИАЛОВ, ПОЛУЧЕННЫХ ПРИ РАСПИЛОВКЕ ТОНКОМЕРНОГО СЫРЬЯ // Современные наукоемкие технологии. 2016. № 9-2. С. 185-190;URL: https://top-technologies.ru/ru/article/view?id=36200 (дата обращения: 25.01.2026).




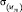 , МПа
, МПа