Теория краевых задач для уравнений смешанного типа в силу теоретической и прикладной важности является одним из интенсивно развивающихся разделов современной теории дифференциальных уравнений с частными производными и привлекает внимание многих исследователей, интересующихся как самой теорией, так и ее приложениями. В частности, многие математические модели тепло- и массообмена в средах, окруженных пористой средой, сводятся к краевым задачам для уравнений смешанного типа.
Необходимость рассмотрения уравнений гиперболо-параболического типа была замечена в 1959 г. И.М. Гельфандом при рассмотрении задачи, связанной с движением газа в канале, окруженном пористой средой. В канале движение описывается волновым уравнением, вне его – уравнением диффузии. Смешанные гиперболо-параболические уравнения лежат в основе математических моделей различных природных явлений. Локальные и нелокальные задачи для таких уравнений встречаются в теории распространения электромагнитных полей, при изучении математических моделей, описывающих влияние растительного покрова на теплообменные процессы в почве и приземном воздухе, при котором возникает необходимость исследования задачи для двух уравнений: уравнения Аллера переноса влаги, предполагающего бесконечную скорость распространения возмущения, и уравнения А.В. Лыкова [6], учитывающего конечную скорость.
Краевые задачи для уравнений нечетного порядка с кратными характеристиками возникают при изучении распространения нелинейных волн в слабодиспергирующих средах.
В настоящее время актуальность исследований нелокальных краевых задач для уравнений смешанного гиперболо-параболического типа второго и более высокого порядков можно обосновать внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, получением новых результатов в теории дробного интегро-дифференцирования, а также их прикладным значением.
Цель исследования – доказать однозначную разрешимость задачи с дробными производными в краевом условии для уравнения смешанного типа третьего порядка с кратными характеристиками, содержащего уравнение А.В. Лыкова в гиперболической части.
Постановка задачи
Рассмотрим уравнение
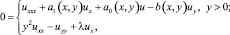 (1)
(1)
где λ – действительная постоянная, причём 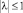 в конечной области Ω ограниченной отрезками AA0, BB0, A0B0 прямых x = 0, x = 1, y = 1, лежащих в полуплоскости y > 0 и характеристиками
в конечной области Ω ограниченной отрезками AA0, BB0, A0B0 прямых x = 0, x = 1, y = 1, лежащих в полуплоскости y > 0 и характеристиками 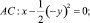
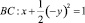 уравнения (1).
уравнения (1).
Пусть 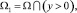

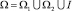 , где I – интервал 0 < x < 1 прямой y = 0.
, где I – интервал 0 < x < 1 прямой y = 0.
Задача.
Требуется найти функцию
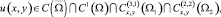
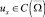
являющуюся решением уравнения (1) при y ≠ 0 и удовлетворяющую условиям
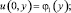
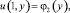 0 ≤ y ≤ 1; (2)
0 ≤ y ≤ 1; (2)
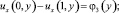 (3)
(3)
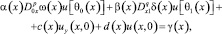 (4)
(4)
где φi(y), i = 1, 2, 3, α(x), β(x), c(x), d(x), γ(x), ω(x), δ(x) – заданные функции, причем 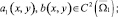
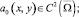
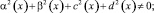
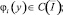
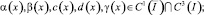 θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) ∈ I с характеристиками AC, BC соответственно,
θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) ∈ I с характеристиками AC, BC соответственно, 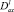 – операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [10].
– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [10].
Задача (1)–(4) относится к классу краевых задач со смещением [7]. Задачи со смещением исследовались в работах [2–4, 7–9].
Теорема. В области Ω не может существовать более одного решения задачи (1)–(4), если
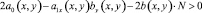 в Ω1, (5)
в Ω1, (5)
где N – постоянная величина, удовлетворяющая условию
 b(x, y) > ρ > 0, b(x, 0) = const ≠ 0; (6)
b(x, y) > ρ > 0, b(x, 0) = const ≠ 0; (6)
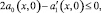 (7)
(7)
а также либо
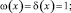
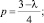
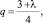 (8)
(8)
и выполняются условия
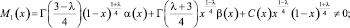 (9)
(9)
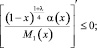
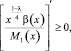 (10)
(10)
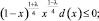 (11)
(11)
либо
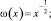
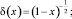
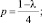
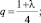 (12)
(12)
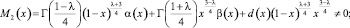 (13)
(13)
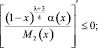
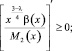
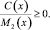 (14)
(14)
Действительно, решение задачи Коши для уравнения (1) в области Ω2 при 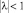 имеет вид [1]
имеет вид [1]
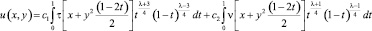 , (15)
, (15)
где 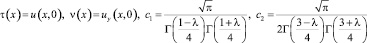 .
.
Удовлетворяя (15) условию (4) при выполнении условий теоремы (12)–(14), получим соотношение между τ(x) и ν(x), принесенное из области Ω2 на I
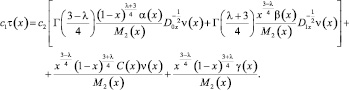 (16)
(16)
Аналогично при выполнении условий (8)–(11)
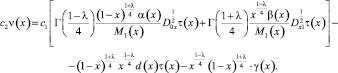 (17)
(17)
Докажем, что решение задачи единственно при выполнении условий (12)–(14). Для этого покажем, что интеграл 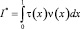 не может быть отрицательным.
не может быть отрицательным.
В самом деле, при γ(x) = 0 из (16) получим соотношение
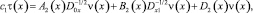
где 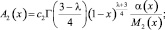
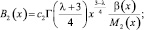
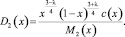
Следовательно,
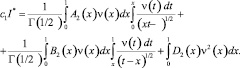
Воспользуемся известной формулой для гамма функции [5]
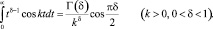
Полагая в ней 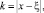
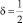 , получим
, получим
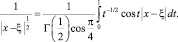
Откуда
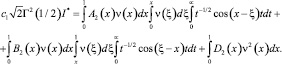
Поменяв порядок интегрирования, а затем интегрируя по частям, в результате несложных вычислений будем иметь
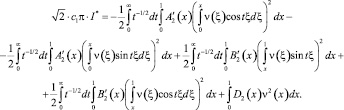 (18)
(18)
При выполнении условий (12)–(14) теоремы единственности I* ≥ 0.
С другой стороны, переходя в уравнении (1) к пределу при y > +0, будем иметь
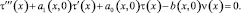 (19)
(19)
Подставляя ν(x) из (19) в 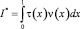 при выполнении условий (5)–(7) теоремы получим
при выполнении условий (5)–(7) теоремы получим
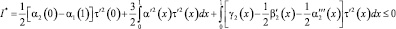 . (20)
. (20)
Отсюда заключаем, что I* = 0. Поскольку слагаемые в правых частях (18) и (20) неотрицательны, то они также равны нулю. В частности, из (18)
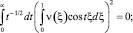
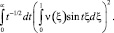
Так как t –1/2 ≥ 0, то 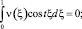
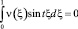 для всех t ∈ (0, ∞) в частности, при t = 2πk, k = 0, 1, 2... При этих значениях t функции sin tξ, cos tξ образуют полную ортогональную систему функций в L2. Следовательно, ν(ξ) = 0 почти всюду, а так как ν(x) непрерывна по условию, то ν(x) = 0 всюду. Отсюда при γ(x) = 0 из (16) получим τ(x) = 0. Таким образом, решение задачи (1)–(4) u(x, y) ≡ 0 в Ω2 как решение Коши (15) с нулевыми данными, а в области Ω1 как решение однородной задачи (1)–(3).
для всех t ∈ (0, ∞) в частности, при t = 2πk, k = 0, 1, 2... При этих значениях t функции sin tξ, cos tξ образуют полную ортогональную систему функций в L2. Следовательно, ν(ξ) = 0 почти всюду, а так как ν(x) непрерывна по условию, то ν(x) = 0 всюду. Отсюда при γ(x) = 0 из (16) получим τ(x) = 0. Таким образом, решение задачи (1)–(4) u(x, y) ≡ 0 в Ω2 как решение Коши (15) с нулевыми данными, а в области Ω1 как решение однородной задачи (1)–(3).
Пусть теперь выполняются условия (9)–(11)теоремы. При γ(x) = 0 из (17) имеем
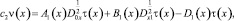
где 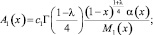
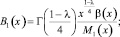
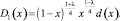
Вводя обозначения 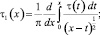
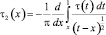 вычислениями, аналогичными предыдущим, получим
вычислениями, аналогичными предыдущим, получим
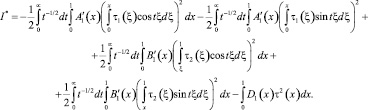
При выполнении условий (9)–(11) теоремы I* ≥ 0 и учитывая (20) можно заключать, что I* = 0. Отсюда следует, что τi(x) = 0, i = 1, 2 и, следовательно τ(x) = 0. Из (17) при γ(x) = 0 имеем ν(x) = 0. Таким образом, как и ранее, u(x, y) ≡ 0 в Ω.
Для доказательства существования решения задачи (1)–(4) проинтегрируем трижды равенство (18). В результате будем иметь
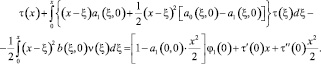 (21)
(21)
При выполнении условий (8)–(9) подставив ν(x) из (18) в (21) получим уравнение
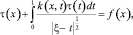 (22)
(22)
где 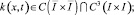
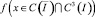
выражаются через известные функции.
Уравнение (22) есть интегральное уравнение Фредгольма второго рода [1], безусловная разрешимость которого в требуемом классе функций следует из единственности решения задачи.
Решение уравнения (22) может быть найдено по формуле
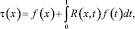
где R(x, t) – резольвента ядра.
При выполнении условий (12)–(13) вопрос разрешимости задачи (1)–(4) также редуцирован к вопросу разрешимости уравнения Фредгольма второго рода относительно ν(x) со слабой особенностью в ядре и гладкой правой частью, безусловная разрешимость которого следует из единственности решения задачи.
Библиографическая ссылка
Кумыков В.К., Водахова В.А., Езаова А.Г. ЗАДАЧА СО СМЕЩЕНИЕМ ДЛЯ УРАВНЕНИЯ СМЕШАННОГО ТИПА ТРЕТЬЕГО ПОРЯДКА С УРАВНЕНИЕМ ВЛАГОПЕРЕНОСА В ГИПЕРБОЛИЧЕСКОЙ ЧАСТИ // Современные наукоемкие технологии. 2016. № 9-1. С. 67-72;URL: https://top-technologies.ru/ru/article/view?id=36179 (дата обращения: 10.03.2026).



