Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Долженкова М.Л. 1 Мельцов В.Ю. 1 Страбыкин Д.А. 1 Чистяков Г.А. 1

---

1 ФГБОУ ВО «Вятский государственный университет»

В работе предложен метод вывода следствий в исчислении предикатов первого порядка на основе исходных правил и фактов базы знаний из новых поступивших фактов. Метод позволяет получать ответ на вопрос: «Какие следствия (выводимые факты) могут быть получены при имеющемся наборе исходных посылок в изменившихся обстоятельствах внешней среды, характеризуемых новыми поступившими фактами?». Практические задачи, сводимые к данной формулировке, возникают в таких областях, как принятие решений, прогнозирование, мониторинг, диагностика, формальная верификация и других. Метод реализует разновидность дедуктивного вывода и базируется на операции деления дизъюнктов. В статье представлены: формальная постановка задачи вывода следствий, описание процедур частичного и полного деления дизъюнктов, процедуры вывода и метода вывода. Работа процедур и метода иллюстрируется на примерах.

Статья в формате PDF

0 KB

вывод следствий

база знаний

поступление новых фактов

исчисление предикатов

дедуктивный вывод

деление дизъюнктов

1. Вагин В.Н. Достоверный и правдоподобный вывод в интеллектуальных системах / В.Н. Вагин, Е.Ю. Головина, А.А. Загорянская, М.В. Фомина. – М.: ФизМатЛит, 2008. – 712 с.

2. Вагин В.Н., Кутепов В.П., Хотимчук К.Ю. Параллельный логический вывода на многоядерном компьютере // Вестник Московского энергетического института. – 2011. – № 3. – C. 82–87.

3. Страбыкин Д.А. Логическое прогнозирование развития ситуаций в интеллектуальных системах на основе дедуктивного вывода. – Киров: Изд-во Вят. гос. ун-та, 2014. – 182 с.

4. Страбыкин Д.А. Логический вывод в системах обработки знаний. – СПб.: Изд-во СПбГЭТУ, 1998. – 164 с.

5. Чери С. Логическое программирование и базы данных / С. Чери, Г. Готлоб, Л. Танка. – М.: Мир, 1992. – 352 с.

6. Элти Дж. Экспертные системы: концепции и примеры / Дж. Элти, М. Кубс. – М.: Финансы и статистика, 1987. – 192 с.

7. Dolgenkova M.L., Chistyakov G.A. Sequences Inference Method out of New Facts by Disjuncts Division in Predicate Calculus (Example) [Электронный ресурс]. – URL: https://zenodo.org/record/57859 (дата обращения 23.08.2007).

8. Meltsov V.Yu. High-Perfomance Systems of Deductive Inference // Yelm, WA. – USA: Science Book Publishing House, 2014. 216 p.

9. Russell S.J. Artificial Intelligence: A Modern Approach / S.J. Russell, P. Norvig // Pearson Education. – 2009. – 1104 p.

Одним из перспективных направлений науки, изучающих методы и алгоритмы искусственного интеллекта, является моделирование рассуждений посредством логики [1]. При этом в качестве формальной системы чаще всего используется исчисление высказываний или исчисление предикатов первого порядка. Логика высказываний позволяет создавать простые для реализации методы логического вывода и, как следствие, разрабатывать программные и программно-аппаратные системы, обладающие высокой производительностью. Однако для описания знания реальной предметной области приходится обращаться к более выразительной формальной системе. Рассуждения, записанные в виде формул исчисления предикатов первого порядка, дают возможность не только задавать всевозможные отношения и причинно-следственные связи между объектами, но и представляются достаточно естественным для человека образом. Все это делает исчисление предикатов удобным средством формализации прикладных задач.

Моделирование рассуждений в интеллектуальных системах осуществляется с помощью аппарата логического вывода [9] – дедуктивного, индуктивного, абдуктивного, нечеткого методов рассуждений на основе аналогий и прецедентов. Данный инструментарий позволяет успешно решать логические задачи. Тем не менее нередко в ходе моделирования сложного, многоступенчатого рассуждения требуется определить следствия, которые могут быть выведены из новых фактов, отражающих обстоятельства изменившейся внешней (окружающей) среды при заданном наборе исходных посылок [3]. Решение поставленной задачи может быть найдено с помощью специализированного вида дедуктивного вывода – параллельного вывода логических следствий.

Вывод следствий

Задачу логического вывода следствий можно сформулировать следующим образом. Имеются исходные непротиворечивые посылки, заданные в виде множества дизъюнктов M = {D1, D2, …, DI}. При этом каждый дизъюнкт содержит один литерал без инверсии. Множество M включает подмножество исходных фактов MF. Кроме того, имеется множество новых фактов mF = {L1, L2, …, Lp, …, LP}. Причем множество M ∪ mF также не противоречиво. Под фактом понимается однолитеральный дизъюнкт без инверсии и аргументов-переменных. Задача вывода логических следствий (литералов без инверсий) формулируется следующим образом.

Требуется определить множество M^S следствий и семейство множеств sH следствий sH = {e0, e1, …, eh, …, eH}. Множество следствий e0 состоит из фактов исходных посылок, совпадающих с новыми фактами: e0 = M^F ∩ m^F. Множество e1 содержит следствия, выводимые за один шаг из множества новых фактов mF на основе множества дизъюнктов посылок M: mF, M ⇒ e1, но не выводимые только из M. Множество следствий eh+1 (h = 1, …, H – 1) включает следствия, выводимые за один шаг из множества следствий eh, новых фактов mF и множества следствий, полученных на предыдущих шагах, на основе множества дизъюнктов посылок M:

eh, mF, ch, M ⇒ e _h+1; ch = c _h–1 ∪ e _h–1, c₀ = ∅.

Семейство множеств следствий s0 = {e0}, а семейство sh (h = 1, …, H) определяется следующим образом:

sh = s ^h–1 ∪ {eh}.

Общее множество следствий MS получается путем объединения множеств семейства sH:

MS = e0 ∪ e1 ∪ … ∪ eH.

Частичное деление дизъюнктов

Частичное деление дизъюнктов выполняется с помощью специальной процедуры образования остатков, которая является одной из основных процедур, используемых в методе логического вывода следствий в исчислении предикатов. Процедура предполагает, что посылки и заключение представлены в виде дизъюнктов. Исходные выражения посылок и заключения в исчислении приводятся к требуемому виду с помощью алгоритмов [4]. Для удобства описания процедуры введем ряд обозначений. w = <b, d, q, n, s> – процедура частичного деления, в которой: b – остаток-делимое (дизъюнкт посылки), используемый для получения остатков; d – остаток-делитель (дизъюнкт заключения), участвующий в образовании остатков; s – множество следствий, полученное в процессе выполнения процедуры; q – частный признак продолжения деления дизъюнктов: «0» – дальнейшее деление возможно; «1» – продолжение деления невозможно; n = {<bt, dt>, t = 1,...,T} – множество пар, состоящих из нового остатка-делимого bt и соответствующего ему остатка-делителя dt, сформированных в результате применения процедуры w. Обозначим также через n^ множество новых остатков-делимых: n^ = {bt, t = 1, ..., T}.

Определим «производную» 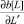дизъюнкта b[L], содержащего литерал L, по литералу L′ дизъюнкта d следующим образом:

а) 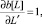если литералы L и LL′ не унифицируются;

б) 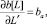если литералы L и LL′ унифицируются. Здесь ba = λb[L]...lL, т.е. представляет собой остаток, получающийся из дизъюнкта b[L] после применения к нему унифицирующей подстановки l и исключения литерала L.

Матрицу «производных» дизъюнкта b по дизъюнкту d определим следующим образом:

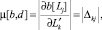
где j = 1, ..., J и k = 1, ..., K, причем J – число литералов в дизъюнкте b, а K – в дизъюнкте d.

Перед выполнением процедуры частичного деления дизъюнктов принимается s = Ø, где s – множество следствий.

В процедуре выполняются следующие действия.

1. Вычисляется матрица «производных» µ[b, d].

Проверяется условие образования остатков. Если все «производные» в матрице µ[b, d] равны единице, то принимается q = 1, n = {<1, 1>}, n^ = {1} и выполняется пункт 5, иначе принимается q = 0 и выполняется следующий пункт.

2. Проверяется наличие следствий. Все элементы матрицы «производных», представляющие собой предикаты без инверсий и аргументов-переменных, являются следствиями и включаются во множество следствий s.

3. Определяется множество n^ новых остатков-делимых. В это множество включаются только различные остатки матрицы µ[b, d], содержащие более одного литерала:

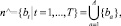
где A – общее число не равных единице, а T – число различных остатков. Если таких остатков нет, то принимается q = 1, n = {<1, 1>}, n^ = {1} и выполняется пункт 5, иначе принимается q = 0 и выполняется следующий пункт.

4. Определяется множество n = {<bt, dt>, t = 1,...,T} пар, состоящих из новых остатков-делимых bt и остатков-делителей dt. Для каждого остатка-делимого bt с помощью подстановки λ_t, использованной при его формировании, вычисляется соответствующий остаток-делитель: dt = λ_t(d...w), где w – вспомогательный дизъюнкт, содержащий исключаемые из остатка d литералы. При вычислении остатка dt из остатка d исключаются литералы 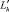, для которых в матрице µ[b, d] выполняется одно из следующих двух условий:

a) 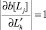для всех j = 1, ..., J; т.е. литералу 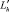в матрице соответствует строка единиц;

б) 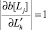для всех j, кроме j = u, такого, что 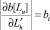; т.е. в строке матрицы, соответствующей литералу 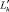все «производные» равны единице, кроме одной, представляющей рассматриваемый остаток bt.

Принимается q = 0 и n = {<bt, dt>, t = 1, ..., T} и выполняется следующий пункт.

5. Фиксируются результаты вычисления процедуры ω.

Пример 1.

Построение матрицы «производных» и формирование остатков рассмотрим на примере вычисления матрицы: µ[b, d], где b = ⌉P(x, y) ∨ O(y, x), d =  ⌉P(b, a).

Для пары дизъюнктов <b, d> выполняется w-процедура.

1. Вычисляется матрица «производных» µ[b, d].

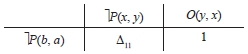
В матрице «производная» Δ₁₁ определяется с помощью унифицирующей подстановки λ₁₁ = {b/x, a/y}:

Δ₁₁= λ₁₁(⌉P(x, y) ∨ O(y, x))...λ₁₁⌉P(b, a) = O(a, b),

а «производная» Δ₁₂ = 1.

Проверяется условие образования остатков. Поскольку в матрице не все «производные» равны единице, то принимается q = 0 и выполняется следующий пункт.

2. Проверяется наличие следствий. Все элементы матрицы «производных», представляющие собой предикаты без инверсий и аргументов-переменных, являются следствиями и включаются во множество следствий s. В рассматриваемом примере Δ₁₁= O(a, b) является следствием: s = {O(a, b)}.

3. Определяется множество n^ новых остатков-делимых. В это множество включаются только различные остатки матрицы, содержащие более одного литерала. Поскольку таких остатков нет, то принимается q = 1, n = {<1, 1>}, n^ = {1} и выполняется пункт 4.

4. Фиксируются результаты вычисления процедуры w. Получено множество следствий s = {O(a, b)}, продолжение частичного деления дизъюнктов невозможно (q = 1).

Полное деление дизъюнктов

Полное деление дизъюнктов направлено на получение всех возможных следствий из множества новых фактов mF на основании исходного дизъюнкта D, множества исходных фактов MF и множества ранее полученных следствий c. Множество следствий вычисляется путем полного деления дизъюнкта D на дизъюнкт d, составленный из инверсий литералов множества mF с помощью рассматриваемой ниже процедуры.

Введем следующие условные обозначения: W = <D, d, MF, c, Q, S> – процедура формирования множества S следствий путем деления дизъюнкта посылки D на дизъюнкт инверсий новых фактов d с учетом множества исходных фактов MF и множества ранее полученных следствий c, в которой Q – признак решения, имеющий два значения: «0» – следствия найдены, «1» – дизъюнкт d не имеет следствий на основании дизъюнкта D.

Формирование множества следствий производится путем многократного применения w-процедур и состоит из ряда шагов. На каждом шаге w-процедуры применяются к имеющимся остаткам-делимым и остаткам-делителям, образуя новые остатки-делимые и новые остатки-делители, которые используются в качестве исходных данных на следующем шаге. Процесс заканчивается, когда на очередном шаге обнаруживается, что во всех w-процедурах данного шага сформированы признаки, свидетельствующие о невозможности продолжения деления дизъюнктов (q = 1).

Описание параллельного выполнения w-процедур осуществляется с помощью специальной индексной функции, обеспечивающей уникальную идентификацию каждой процедуры и ее параметров. Введем индексную функцию i(h) для индекса размером h, которую определим для индексной переменной t индуктивно следующим образом:

i(1) = t, t = 1, ..., T;

i(2) = i(1).ti(1), ti(1) = 1, ..., Ti(1) (t.tt = 1.t1, t1 = 1, …, T1, 2.t2, t2 = 1, …, T2, …, T.tT, tT = 1, …, TT);

i(3) = t.tt.tE (E = t.tt),

i(3) = i(2).ti(2), ti(2) = 1, ..., Ti(2); и т.д.

В общем случае

i(h) = i(h – 1).ti(h-1), ti(h–1) = 1,...,Ti(h–1).

Будем считать, что i(0) означает отсутствие индекса у индексируемой переменной, например Ti(0) = T, а также, что i(1) = i(0).ti(0) = t.

Индексная функция i(h) задает индекс, который (при h > 1) состоит из константы, формируемой на основе значения функции i(h – 1), и соответствующей этой константе переменной ti(h–1). Множество индексов, описываемых с помощью функции i(h), формируется на основе значений функции i(h – 1) и соответствующих им значений переменных ti(h–1) = 1, ..., Ti(h–1). Например, при T = T1 = 3, T2 = 2 получим i(1) = t, t = 1, 2, 3; i(2) = 1.t1, t1 = 1, 2, 3 2.t2, t2 = 1,2. То есть i(2) = 1.1, 1, 2, 1.3, 2.1, 2.2.

1. Подготовительный шаг. На подготовительном шаге процедуры полного деления дизъюнктов к дизъюнкту посылки D и дизъюнкции инверсий новых фактов d применяется процедура образования остатков w = <D, d, q, n, s>, и анализируется частный признак продолжения деления дизъюнктов q. Если q = 1 (продолжение деления невозможно), то принимается S = s, при этом, если s ≠ Ø, то устанавливается Q = 0, иначе Q = 1, и выполняется заключительный шаг (пункт 3). Если же q = 0, то новые пары остатков, сформированные во множестве 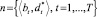выступают в качестве исходных данных для w-процедур на основном шаге. Причем, при первом выполнении основного шага в качестве остатков-делителей вместо дизъюнктов 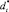используются дизъюнкты dt. Дизъюнкт dt образуется путем дополнения дизъюнкта 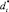инверсиями литералов множества исходных фактов MF и инверсиями литералов множества ранее полученных следствий с. Кроме того, при первом выполнении основного шага принимается S0 = s.

Используя индексную функцию, множество n можно представить следующим образом:

ni(h) = {<bi(h+1), di(h+1)>, i(h + 1) = i(h).ti(h); ti(h) = 1, ..., Ti(h)},

где h = 0.

2. Основной шаг. При k-м выполнении основного шага (k = 1, 2, ..., K) для каждой пары остатков <bi(h+1), di(h+1)> всех множеств ni(h) таких пар (h = k –1), полученных на предыдущем шаге:

ni(h) = {<bi(h+1), di(h+1)>, i(h + 1) = i(h).ti(h); ti(h) = 1, ..., Ti(h)},

выполняется w-процедура:

ω_i(h+1) = <bi(h+1), di(h+1), qi(h+1), ni(h+1), si(h+1)>, i(h + 1) = i(h).ti(h); ti(h) = 1, ..., Ti(h).

Производится пополнение множества следствий:

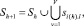
где v = ti(h), V = Ti(h).

Если S _h+1 ≠ Ø, то устанавливается Qh+1 = 0, иначе Qh+1 = 1. Анализируются частные признаки решения qi(h+1). Если нет ни одного qi(h+1) = 0, то принимается Q = Qh+1, S = Sh+1 и выполняется пункт 3. Иначе выделяются новые множества пар остатков, полученные при текущем выполнении основного шага:

ni(h+1) = {<bi(h+2), di(h+2)>, i(h + 2) = i(h + 1).ti(h+1); ti(h+1) = 1, ..., Ti(h+1)},

и осуществляется переход к (k + 1) выполнению основного шага (пункт 2), для которого эти множества выступают в качестве исходных.

3. Заключительный шаг. Фиксируются результаты вычисления процедуры W: признак решения Q и множество следствий S.

Вместо процедуры формирования остатков Ω иногда будем использовать специальную операцию, которую назовем операцией полного деления дизъюнктов для получения следствий. Результат такой операции вычисляется с помощью процедуры формирования остатков и представляет собой конъюнкцию литералов b1, b2, ..., bK, полученных во множестве S. Полное деление дизъюнкта D на дизъюнкт d будем записывать так: DΩd = b1b2...bK. Будем считать, что если в W-процедуре Q = 1 (S = Ø), то DΩd = 1.

Рассмотрим полное деление дизъюнктов на следующем примере.

Пример 2.

Проиллюстрируем полное деление дизъюнктов (выполнение W-процедуры) на примере. Исходными данными являются следующие предложения [6].

1) нравится (Джилл, вино): 1 > P(a, c);

2) нравится (Джон, еда): 1 > P(b, е);

3) нравится (Джон, вино): 1 > P(b, с);

4) нравится (y, вино)&мужчина(x) > провожатый (x, y):

P(y, c)P1(x) > R(x, y)

или

1 → ⌉P(y,c) ∨ ⌉P1(x) ∨ R(x, y);

5) Новый факт: мужчина (Джон): 1 → P1(b).

В процедуре Ω = <D, d, M^F, c, Q, S> полного деления дизъюнктов в качестве дизъюнкта-делимого D будет выступать дизъюнкт посылки (4):

D = ⌉P(y, c) ∨ ⌉P1(y) ∨ R(x, y),

а в качестве дизъюнкта-делителя – отрицание нового факта (5): d = ⌉P1(b). Кроме того

MF = {P(a, c), P(b, е), P(b, с)}, c = Ø.

1. Подготовительный шаг. Для пары дизъюнктов

<b, d>,

где b = ⌉P(y, c) ∨ ⌉P1(x) ∨ R(x, y), d = ⌉P1(b), выполняется w-процедура. Вычисляется матрица «производных»:

В матрице «производные» Δ₁₁ = Δ₁₃= 1, а «производная» Δ₁₂ определяется с помощью унифицирующей подстановки λ₁₂ = {b/x}:

Δ₁₂ = λ₁₂ (⌉P(y, c) ∨ ⌉P1(x) ∨ R(x,y))...λ₁₂P1(b) = ⌉P(y, c) ∨ R(b, y) = b1.

Получен остаток b1 не равный единице, поэтому принимается q = 0 и происходит формирование исходных данных для основного шага: n = { < b1,d1 > }. Дизъюнкт d1 образуется путем дополнения дизъюнкта 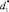инверсиями литералов множества исходных фактов M^F и инверсиями литералов множества ранее полученных следствий с. В данном случае дизъюнкт 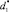получается из дизъюнкта d в результате исключения литерала, которому в матрице соответствует строка, содержащая только одну не равную единице «производную», представляющую остаток b1. Таким образом, получаем: 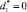, а d1 = ⌉P(a, c) ∨ ⌉P(b, e) ∨ ⌉P(b, c). Поскольку в матрице «производных» однолитеральных остатков с предикатами без инверсий нет, то s = Ø.

2. Основной шаг (первое выполнение, h = 0, S0 = s = Ø). Для пары остатков

<b1, d1>,

где

b1 = ⌉P(b, c) ∨ R(x, b),

d1 = ⌉P(a, c) ∨ ⌉P(b, e) ∨ ⌉P(b, c),

выполняется ω-процедура:

В матрице «производные» Δ₁₂ = Δ₂₁= Δ₂₂= Δ₃₂= 1. А две «производные» отличны от единицы: Δ₁₁= R(b, a) при λ₁₁ = {a/y} и Δ₃₁ = R(b, b) при λ₃₁ = {b/y}. То есть получены «производные», представляющие собой следствия, поэтому данные предикаты включаются во множество следствий s = {R(b, a), R(b, b)}. Производится пополнение множества следствий: S1 = S0 ∪ s = {R(b, a), R(b, b)}. Поскольку S1 ≠ Ø, то устанавливается Q1 = 0. Анализируется частный признак решения q1. Остатков, содержащих более одного литерала, в матрице «производных» нет, поэтому принимается q1 = 1, Q = Q1, S = S1 и выполняется пункт 3.

3. Заключительный шаг. Фиксируются результаты вычисления процедуры W: признак решения Q = 0 и множество следствий S = {R(b, a), R(b, b)}. Таким образом, DΩd = R(b, a)&R(b, b).

Полученные следствия означают, что из нового факта мужчина (Джон) на основе исходных посылок (1–4) следует, что Джон является провожатым Джилл, а также провожатым «самого себя».

Процедура вывода следствий

Процедура вывода следствий является аналогом процедуры деления дизъюнктов, используемой в логике высказываний [3]. Процедура позволяет сделать шаг вывода, преобразуя выводимый дизъюнкт в новый выводимый дизъюнкт, необходимый для продолжения вывода на следующем шаге. Введем следующие условные обозначения.

Для вывода следствий текущего шага используется специальная процедура

v = <M, R, o, p, R1, e>,

в которой: M = {D1, D2, …, Di, …, DI} – множество дизъюнктов исходных секвенций; – дизъюнкт i-й секвенции, состоящий из литералов 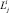; R = ⌉L1 ∨ ⌉L2 ∨ ... ∨ ⌉Lk ∨ ... ∨ ⌉LK – выводимый дизъюнкт, состоящий из инверсий литералов Lk ранее полученных следствий, а на первом шаге – новых фактов; p – признак продолжения вывода: «0» – дальнейший вывод возможен; «1» – вывод завершен; R1 – новый выводимый дизъюнкт; o = <c, C> – пара множеств текущих следствий, состоящая из множеств следствий, образованных до выполнения (c) и после выполнения (C) процедуры; e – множество следствий для выводимого дизъюнкта.

Процедура вывода использует в качестве субпроцедуры ранее рассмотренную Ω-процедуру полного деления дизъюнктов.

Процедура вывода применима, если M ≠ Ø и Ji, K ≥ 1 (i = 1, ..., I), иначе сразу устанавливается признак p = 1, e = Ø, C = c и производится переход к п. 5. В процедуре выполняются следующие действия.

1. Выполняется полное деление дизъюнктов.

1) Дизъюнкты исходных секвенций с помощью Ω-процедур делятся на выводимый дизъюнкт: DiΩR = Bi, i = 1, ..., I. Причем Bi = 1, если признак Qi = 1 и Bi представляет собой конъюнкцию следствий, полученных во множестве Si: Bi = bi1&…&bik&...&biK, – в противном случае.

2) Анализируются признаки решений Qi, выполненных Ω-процедур. Если все признаки решений равны единице, то принимается p = 1, e = Ø, C = c и производится переход к п. 5, иначе выполняется следующее действие.

2. Формируется множество следствий для выводимого дизъюнкта. Множество e образуется путем объединения множеств следствий, полученных при выполнении W-процедур. Если e ≠ Ø, то из полученного множества следствий исключаются поглощаемые следствия. Литерал b поглощается литералом a, тогда и только тогда, когда имеется такая подстановка λ, что b ⊆ λa. При этом в качестве поглощающих литералов используются не только следствия из множества e, но и следствия из множества c, полученные на предыдущем шаге вывода следствий. Если в процессе поглощения литералов из множества e будут исключены все литералы, то принимается e = Ø, C = c, p = 1 и производится переход к п. 5, иначе устанавливается p = 0 и выполняется следующее действие.

3. Формируется новый выводимый дизъюнкт. Выводимый дизъюнкт R1 представляет собой дизъюнкцию инверсий литералов множества следствий e.

4. Формируется новое множество следствий. В паре множеств текущих следствий o = <c, C> множество C образуется в результате объединения множества следствий с, полученного до выполнения процедуры и множества следствий e, полученного после исключения поглощаемых литералов: С = c ∪ e.

5. Фиксируются результаты выполнения процедуры. Если признак p = 1, то дальнейший вывод следствий невозможен, а если p = 0, то вывод может быть продолжен. При непустом множестве следствий e в процессе выполнения процедуры будут сформированы: новый выводимый дизъюнкт R1 и новое множество следствий C.

Следует отметить, что в процедурах вывода деление дизъюнктов исходных посылок на дизъюнкт R может производиться параллельно.

Метод вывода следствий

Метод вывода следствий основан на процедуре вывода следствий и состоит из ряда шагов, на каждом из которых выполняется процедура вывода v, причем результаты выполнения процедуры текущего шага становятся исходными данными для процедуры следующего шага. Процесс заканчивается в случае, если дальнейший вывод следствий невозможен (получено значение признака p = 1).

Обозначим через h номер шага вывода, а через P – общий признак продолжения вывода (P = 0 – продолжение вывода возможно, P = 1 – продолжение вывода невозможно). Тогда описание метода может быть представлено в следующем виде.

1. Определение начальных значений: h = 1, M ≠ Ø, m^F ≠ Ø. Формирование выводимого дизъюнкта R1, состоящего из литералов Lk, представляющих собой инверсии литералов множества mF. Определение множества следствий e0, совпадающих с фактами MF, имеющимися в исходных посылках: e0 = M^F ∩ m^F, s0 = {e0}, c1 = e0. Установка начального значения общего признака продолжения вывода: P0 = 0.

2. Выполнение h-й процедуры вывода

v_h = <M, Rh, oh, ph, R _h+1, e_h>.

3. Формирование семейства следствий и проверка признаков. Производится формирование семейства множеств следствий s^h = s ^h–1 ∪ {eh}. Формирование общего признака продолжения вывода P_h = P _h–1 ∨ p_h. Если Ph = 0, то вывод продолжается: h увеличивается на единицу, принимается сh+1 = Ch и производится переход к п. 2, иначе вывод завершается (h = H). Полученные следствия содержатся во множествах семейства sH, и общее множество следствий вычисляется путем объединения этих множеств:

M^S = e0 ∪ e1 ∪ e2 ∪ … ∪ eH.

Пример 3.

Применение метода вывода следствий рассмотрим на примере о родственных связях, представленном в работе [5]. Исходными данными являются следующие предложения.

Отец (F) – это персона (Per) мужского пола, являющаяся родителем (P). Дед (GF) – это отец родителя. Родные братья или сестры (S) – это две различных (N) персоны, которые имеют общего родителя. Тетя (A) – это персона, которая является родной сестрой родителя. Известно, что Дмитрий (a) является родителем Виктории (b), Владимир (с) является родителем Натальи (d), Дмитрий – мужчина (m), а Виктория – женщина (f). Новыми фактами является то, что Владимир – ребенок Дмитрия, и Владимир и Виктория – разные люди.

Формальная постановка задачи выглядит следующим образом.

1) F(x, y) ∨ ⌉Per(x, m) ∨ ⌉P(x, y);

2) GF(x, y) ∨ ⌉F(x, z) ∨ ⌉P(z, y);

3) S(x, y) ∨ ⌉P(z, x) ∨ ⌉P(z, y) ∨ ⌉N(x, y);

4) A(x, y) ∨ ⌉Per(x, f) ∨ ⌉P(z, y) ∨ ⌉S(x, z);

5) P(a, b); P(c, d);

6) Per(a, m):

7) Per(b, f);

8) P(a, c), N(b, c).

Логический вывод будет состоять из следующих шагов.

Определение начальных значений:

h = 1, M = {D1, D2, D3, D4},

mF = {P(a, c), N(b, c)}.

Формирование выводимого дизъюнкта R1 = ⌉P(a, c) ∨ ⌉N(b, c), состоящего из литералов, представляющих собой инверсии литералов множества mF. Определение множества следствий e0, совпадающих с фактами MF, имеющимися в исходных посылках:

e0 = M^F ∩ m^F = Ø, s⁰ = {e0}, c₁ = e₀ = Ø.

Установка начального значения общего признака продолжения вывода: P₀ = 0.

Результаты выполнения процедур вывода представлены в таблице. Полное описание выполняемых действий содержится в работе [7].

Результаты выполнения процедур вывода

Общее множество следствий получается путем объединения множеств семейства s3: MS = {F(a, c), S(b, c), GF(a, d), A(b, d)}.

Таким образом, в процессе вывода следствий было установлено, что Дмитрий является отцом Владимира (F(a, c)), Владимир и Виктория – единокровные брат и сестра (S(b, c)), у Дмитрия есть внучка Наталья (GF(a, d)), а у Натальи – тетя Виктория (A(b, d)).

Заключение

Предложенный метод логического вывода позволяет находить следствия из вновь появившихся фактов на основе базы знаний, представленной формулами исчисления предикатов первого порядка. Метод имеет две особенности: вывод следствий осуществляется из новых фактов, поступающих дополнительно к используемой базе знаний; следствиями считаются предикаты без инверсии, не содержащие переменных. Особенности метода обусловлены его первоначальной ориентацией на задачи логического прогнозирования развития ситуаций. При формализации таких задач новые факты отражают изменение текущего состояния ситуации, а последовательность множеств следствий, соответствующая глубине логического вывода, используется для прогнозирования развития ситуации.

Метод обладает многоуровневым параллелизмом (параллельная унификация пар литералов, одновременное и независимое формирование остатков и единовременное деление дизъюнктов базы знаний на выводимый дизъюнкт), что позволяет эффективно применять его при реализации интеллектуальных систем на современных высокопроизводительных параллельных вычислительных платформах [2, 8].

Работа выполнена при финансовой поддержке РФФИ (проект № 15-01-02818a).

Библиографическая ссылка