Диагностирование сложных технических объектов выполняется посредством анализа разнообразных параметров, выявляющих электрические и неэлектрические дефекты. По характеру измерения, все параметры могут быть разделены на дискретные, измеряемые в фиксированный момент времени, и непрерывные, представляющие собой изменение некоторого параметра во времени. Наиболее распространенными непрерывными диагностическими параметрами являются шум, вибрация и ток. Оценка текущего состояния объекта и поиск возникших неисправностей осуществляется с применением различных методов анализа сигналов. Одним из наиболее простых и доступных является метод спектрального анализа сигнала с применением Фурье-преобразования [3], которое разлагает произвольный сигнал на элементарные гармонические колебания с различными частотами, а все необходимые свойства и зависимости выражаются с помощью одной базисной функции exp(jωt) (1) или двух действительных функций sin(ωt) и cos(ωt) (2).
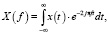 (1)
(1)
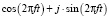 , (2)
, (2)
где t – время, с; x – сигнал во временной области; X – сигнал в частотной области, f – частота полученного сигнала.
Для решения данной проблемы предложено оконное преобразование Фурье, в котором вводится движущаяся вдоль независимой переменной (пространство или время) оконная функция, имеющая компактный носитель [5]. Ширина окна выбирается в несколько раз меньше длительности сигнала. Оконное преобразование Фурье сопоставляет исходному сигналу функцию двух переменных – частоты и положения окна (временное или координатное). При всех своих возможностях оконному преобразованию Фурье присущи проблемы, исходящие из явления, которое называется принципом неопределенности Гейзенберга [4]. Проблема состоит в том, что размер окна выбирается постоянным для анализа всего сигнала, тогда как разные его участки могут требовать применения разных окон. Если сигнал состоит из далеко отстоящих друг от друга частотных компонент, то можно пожертвовать спектральным разрешением в пользу временного разрешения, и наоборот.
Также к числу недостатков Фурье-преобразования относятся:
1. Преобразование Фурье дает частотную информацию, содержащуюся в сигнале, то есть говорит о том, каково содержание каждой частоты в сигнале, но не позволяет определить момент времени возникновения и окончания этой частоты.
2. Ограниченная информативность анализа нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей), т.к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков и т.п.) по всему частотному диапазону спектра. Появляются «паразитные» высокочастотные составляющие, явно отсутствующие в исходном сигнале при наличии в нём скачков и разрывов.
3. Гармонические базисные функции разложения не способны отображать перепады сигналов с бесконечной крутизной типа прямоугольных импульсов, т.к. для этого требуется бесконечно большое число членов ряда. При ограничении числа членов ряда Фурье в окрестностях скачков и разрывов при восстановлении сигнала возникают осцилляции (явление Гиббса).
4. Преобразование Фурье отображает глобальные сведения о частотах исследуемого сигнала и не дает представления о локальных свойствах сигнала при быстрых временных изменениях его спектрального состава. Так, например, преобразование Фурье не различает стационарный сигнал с суммой двух синусоид от нестационарного сигнала с двумя последовательно следующими синусоидами с теми же частотами, т.к. спектральные коэффициенты вычисляются интегрированием по всему интервалу задания сигнала. Преобразование Фурье не имеет возможности анализировать частотные характеристики сигнала в произвольные моменты времени.
5. Используя преобразование Фурье, можно работать с сигналом либо только во временной, либо только в частотной области. Одновременно получить частотно-временное представление, используя классический алгоритм преобразования Фурье, нельзя (отсутствует возможность получения информации о том, какие частоты присутствуют в сигнале в данный момент времени).
6. Анализ частот, полученных в результате Фурье-разложения для целей диагностирования, достаточно сложен и требует привлечения опытного специалиста – диагноста, что влечет дополнительные расходы.
Данных недостатков лишено вейвлет-преобразование. Термин «вейвлет» (wavelet) в переводе с английского означает «маленькая (короткая) волна». Вейвлеты – это обобщенное название семейств математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой, порождающей функции посредством ее сдвигов и растяжений по оси времени. Все вейвлеты конкретного семейства ψab(t) имеют то же число осцилляций, что и материнский вейвлет ψ(t), поскольку получены из него посредством масштабных преобразований (a) и сдвига (b).
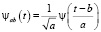 . (3)
. (3)
Вейвлет-преобразование сигнала – это его представление в виде обобщенного ряда или интеграла Фурье по системе базисных функций, сконструированных из материнского (исходного) вейвлета ψ(t), обладающего определенными свойствами, за счет операций сдвига во времени (b) и изменения временного масштаба (a). Множитель 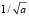 обеспечивает независимость нормы этих функций от масштабирующего числа a [1]. Малые значения а соответствуют мелкому масштабу ψab(t) или высоким частотам – большие параметры a – крупному масштабу ψab(t), т.е. растяжению материнского вейвлета ψ(t) и сжатию его спектра.
обеспечивает независимость нормы этих функций от масштабирующего числа a [1]. Малые значения а соответствуют мелкому масштабу ψab(t) или высоким частотам – большие параметры a – крупному масштабу ψab(t), т.е. растяжению материнского вейвлета ψ(t) и сжатию его спектра.
Возможности вейвлет-преобразования во многом определяются параметрами материнской функции ψ. Существуют три основных семейства вейвлетов. К первой группе относятся вейвлеты, использующие временную локализацию (вейвлеты Гаусса, Морле и др.). Второй тип вейвлетов (вейвлет Мейера) использует локализацию по частоте.
Таблица 1
Характерные неисправности и частоты диагностирования электродвигателя
|
Неисправность двигателя |
Характерные частоты Фурье-анализа |
|
Износ или повреждение щеток |
|
|
Обрыв или износ коллекторной обмотки |
|
|
Наличие переменной составляющей в напряжении питания |
|
|
Небаланс ротора |
|
|
Износ подшипников электродвигателя |
|
|
где k – номер гармоники; kщ – количество щеток электродвигателя; fвр – частота вращения ротора электродвигателя, р – число пар полюсов электродвигателя, fП – частота питающей сети переменного тока; |
|
Таблица 2
Результаты замера виброскорости в трех ортогональных направлениях
|
Определяющий параметр диагностирования |
Без введения неисправностей |
С введенной неисправностью |
||||
|
вертикальная |
горизонтальная |
осевая |
вертикальная |
горизонтальная |
осевая |
|
|
СКЗ виброскорости, мм/с |
1,1 |
1,135 |
1,048 |
5,103 |
2,144 |
4,029 |
Таблица 3
Амплитуды виброскорости на характерных частотах диагностирования
|
Характерные частоты |
Без введения неисправностей |
С искусственно созданной неисправностью |
||||
|
вертикальная, (мм/с) |
горизонтальная, (мм/с) |
осевая, (мм/с) |
вертикальная, (мм/с) |
горизонтальная, (мм/с) |
осевая, (мм/с) |
|
|
Щеточная |
0,2 |
0,2 |
0,17 |
1,25 |
0,3 |
0,4 |
|
Коллекторная |
0,15 |
0,15 |
0,01 |
0,32 |
0,02 |
0,32 |
|
Небаланса ротора |
0,07 |
0 |
0,57 |
0,23 |
1,8 |
1,73 |
|
Подшипниковые |
0,2 |
0,68 |
0,1 |
0,42 |
0,88 |
0,2 |
|
Составляющие сети |
0,17 |
0,1 |
0,35 |
0,7 |
0,1 |
1,37 |
При этом для первого типа вейвлетов характерна потеря информации о частотной составляющей сигнала, а при использовании второго типа вейвлетов не фиксируется локализация сигнала по времени.
Третий тип вейвлетов определяется фильтрами, называемыми квадратурными зеркальными фильтрами (КЗФ), представляющими собой некоторую функцию, с помощью которой рассчитывается преобразование сигнала (прямое и обратное) путем вычисления свертки сигнала в каждой его точке с этой функцией, называемой фильтром. Квадратурные зеркальные фильтры – фильтры с конечной импульсной характеристикой, частотная характеристика которых симметрична относительно половины частоты дискретизации. К таким функциям относятся вейвлеты Добеши, Симлет, вейвлеты Лемарье и другие. Для решения задачи поиска неисправностей путем анализа непрерывных параметров необходимо фиксировать локализацию сигнала и по частоте и по времени, следовательно, применять квадратурные зеркальные фильтры. Из всех существующих вейвлетов данной группы наиболее соответствуют вышеперечисленным условиям вейвлеты Добеши [2], поэтому именно их целесообразно применять в качестве материнского вейвлета для поиска неисправностей.
В настоящее время накоплен значительный объем знаний по поиску неисправностей с применением Фурье-преобразований, рассчитаны характерные частоты для всех основных неисправностей. Для использования этих знаний при вейвлет-анализе сигналов необходимо произвести перерасчет частоты Фурье в масштаб вейвлета [4], анализ которого позволит локализовать неисправность c помощью вейвлет-признаков. Основными из них являются сумма (накопление) и энергия вейвлет-коэффициентов. Если вейвлет-коэффициенты меньше единицы, то их энергия будет меньше суммы вейвлет-коэффициентов. Исходя из этого, для определения неисправности необходимо найти сумму и энергию вейвлет-коэффициентов на характерных масштабах и сравнить с аналогичными для исправного объекта. Для установления взаимосвязи между этими показателями необходимо провести ряд экспериментальных исследований.
Объектом диагностирования является двигатель постоянного тока типа ПЯ 250Ф, применяющийся в качестве исполнительного двигателя роботов, в системах автоматического регулирования плоскошлифовальных, режущих, шприцевых, фрезерных станков, в станках для плазменной резки, в крутильных машинах, мехатронных модулях, автоматических линиях, следящих приводах, в робототехнике и другом высокоточном оборудовании. Основные неисправности и характерные частоты приведены в табл. 1.
Для анализа результатов измерения вибрации необходимо выполнить амплитудный и спектральный анализ полученных результатов. Амплитудный анализ представляет собой оценку измеренных среднеквадратических значений (СКЗ) абсолютной виброскорости. В случае, если замеренные значения СКЗ лежат в пределах нормы, объект диагностирования является исправным или работоспособным и выполнение спектрального анализа не требуется. Если значение СКЗ виброскорости превышает нормируемое, то объект диагностирования неработоспособен.
Согласно ГОСТ ИСО 10816-1-97 двигатель ПЯ250Ф относится к первому классу машин. Результаты измерения СКЗ вибрации исправного эталонно двигателя и с искусственно созданной неисправностью представлены в табл. 2.
Из табл. 2 видно, что эталонный двигатель является пригодным для дальнейшей эксплуатации и согласно ГОСТ ИСО 10816-1-97 относится к классу А, следовательно, может эксплуатироваться без ограничения сроков.
Двигатель с искусственно созданной неисправностью согласно ГОСТ ИСО 10816-1-97 относится к классу В, следовательно, непригоден для длительной эксплуатации.
Найти возникшие неисправности можно с помощью спектрального анализа амплитуд сигнала на характерных частотах (табл. 1). Если на какой-либо частоте амплитуда сигнала в 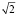 раз превышает аналогичную для заведомо исправного эталонного двигателя, то произошел отказ по причине данной неисправности. При оценке технического состояния диагностируемого электродвигателя учитываются показания датчиков, измеряющих вибрацию в трех взаимно перпендикулярных направлениях. Амплитуды виброскорости на характерных частотах диагностирования приведены в табл. 3.
раз превышает аналогичную для заведомо исправного эталонного двигателя, то произошел отказ по причине данной неисправности. При оценке технического состояния диагностируемого электродвигателя учитываются показания датчиков, измеряющих вибрацию в трех взаимно перпендикулярных направлениях. Амплитуды виброскорости на характерных частотах диагностирования приведены в табл. 3.
Из табл. 3 видно, что происходит резкое увеличение амплитуды виброскорости для щеточной частоты при вертикальном измерении, следовательно, причиной неисправности является неисправность щеток. Из проведенного эксперимента следует, что спектральный анализ частотного сигнала, полученного посредством Фурье-преобразования, позволяет найти неисправность объекта. Однако такой способ весьма трудоемок, требует привлечения специалиста-эксперта и не может быть применен для автоматизации процесса диагностирования.
Альтернативой преобразования Фурье является вейвлет-преобразование. Сопоставление частоты и масштаба вейвлет-преобразования для частоты вращения двигателя представлено в табл. 4. На рисунке представлен результат расчета суммы и энергии вейвлет-коэффициентов исправного и неисправного двигателя.
Из полученных графиков видно, что на масштабах, соответствующих неисправностям щеток, происходит рост энергии и падение суммы вейвлет-коэффициентов. Данная зависимость свидетельствует о наличии данной неисправности.
Таблица 4
Взаимосвязь между частотой Фурье-преобразования и масштабом вейвлета
|
Неисправность электродвигателя |
Частота Фурье-преобразования, Гц |
Масштаб вейвлета |
|
Износ или повреждение щеток |
39,3 43,3 47,3 |
35 32 29 |
|
Обрыв или износ коллекторной обмотки |
141,2 282,42 423,624 |
9 5 3 |
|
Наличие переменной составляющей в напряжении питания |
50 100 150 |
27 14 9 |
|
Небаланс ротора |
17,65 11,767 8,8256 |
77 117 154 |
|
Износ подшипников электродвигателя |
819 1228,5 14,12 |
2 1 97 |
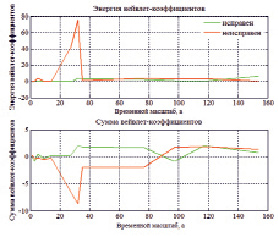
Энергия и сумма вейвлет-коэффициентов виброскорости исправного и диагностируемого электродвигателей
Выводы
Произведено теоретическое и экспериментальное сравнения наиболее популярных методов анализа непрерывных диагностических сигналов: быстрое преобразование Фурье и вейвлет-преобразование. Показано что, оба метода позволяют найти неисправности объекта, но вейвлет-преобразование не требует привлечения специалистов-экспертов, что делает его более эффективным для применения в системах автоматического диагностирования.
Библиографическая ссылка
Круглова Т.Н., Шурыгин Д.Н., Литвин Д.А., Тарковалин С.А., Власов А.С., Рыженков С.И., Арцебашев В.В. ОЦЕНКА ЭФФЕКТИВНОСТИ РАЗЛИЧНЫХ МЕТОДОВ АНАЛИЗА ВРЕМЕННЫХ ДИАГНОСТИЧЕСКИХ СИГНАЛОВ // Современные наукоемкие технологии. 2016. № 8-2. С. 237-241;URL: https://top-technologies.ru/ru/article/view?id=36135 (дата обращения: 27.02.2026).




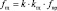
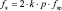
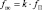
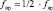 ,
, 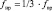 ,
, 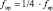
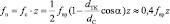
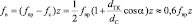
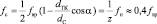
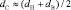 – диаметр сепаратора, dH – наружный диаметр подшипника; dB – внутренний диаметр подшипника; dТK – диаметр тела качения; α – угол контакта тел качения с дорожками качения; z – число тел качения.
– диаметр сепаратора, dH – наружный диаметр подшипника; dB – внутренний диаметр подшипника; dТK – диаметр тела качения; α – угол контакта тел качения с дорожками качения; z – число тел качения.