При решении задач обеспечения навигационной безопасности движения в судопотоках высокой интенсивности и неоднородности возникает необходимость обладания максимально полной информацией о свойствах движения каждого объекта [5, 7]. Существующие системы диспетчеризации движения судов ориентированы на традиционную работу в двумерном навигационном пространстве. Вместе с тем, в условиях регулярного присутствия над оживленной акваторией маловысотных низкоскоростных воздушных объектов (вертолетов) обостряется проблема генерации ложных тревог (воздушные объекты принимаются за морские).
Диспетчерскими службами крупных морских портов отмечается значительное повышение интенсивности воздушного движения, осуществляемого средствами малой авиации и связанного с выполнением лоцманских, таможенных и пограничных функций. Указывается на возрастание психологической нагрузки на диспетчерский персонал, вынужденный принимать решения в условиях неопределённости навигационной обстановки, осложняемой вероятностью присутствия воздушных объектов. В обсуждаемом контексте ошибочное заключение судоводителя или оператора СУДС о воздушной цели как о морской (когда их скорости движения сравнимы) может в корне исказить представления о навигационной обстановке и привести к ошибочным управленческим решениям.
Указанная проблема частично решается применением Автоматической идентификационной системы (АИС) на воздушном объекте: информация АИС позволяет, в том числе, однозначно идентифицировать тип цели [6]. Вместе с тем, транспондерами АИС оснащаются далеко не все воздушные объекты, допускающие полет над акваторией. Рассматриваемый прикладной аспект требует решения задачи селекции воздушных объектов путем расширения навигационных функций систем, образуемых на основе двухкоординатных радаров. Другими словами, актуальна постановка задачи наблюдения трёхмерного навигационного пространства на базе двухкоординатных измерителей.
Проблема трехкоординатного наблюдения воздушных объектов двухкоординатными измерителями неоднократно привлекала внимание исследователей. Так, в работах [8, 9] рассматривается способ определения высоты объекта по измерениям его дальности и азимута несколькими РЛС путем решения геометрической задачи.
В работе [10] была показана принципиальная возможность (хотя и с ограниченным эффектом) решения трехкоординатной задачи при использовании даже одного двухкоординатного радара. Сущность рассмотренной методики состоит в использовании линейного динамического алгоритма оптимального оценивания, обрабатывающего измерения дальности и азимута объекта последовательно, по мере их поступления и основанном на дискретном фильтре Калмана. Если в системе имеется несколько радаров, то после отдельной обработки измерений каждой РЛС производится дополнительная совместная обработка полученных оценок высоты объекта.
В работах [1–4] была показана характерная особенность задачи – нерегулярность оценок высоты наблюдаемого объекта, затрудняющая принятие решения об отнесении объекта к классу «надводный/воздушный». Были предложены различные варианты доопределения исходной модели задачи как задачи селекции воздушных объектов.
В контексте проблемы обеспечения навигационной безопасности движения представляет интерес аналитическое исследование модельных представлений задачи наблюдения воздушных объектов с помощью одного или нескольких двухкоординатных радаров на предмет принципиальной разрешимости (наблюдаемости). Настоящая статья посвящена теоретическому обоснованию корректности постановки задачи на различных классах траекторий движения объектов.
Основные модельные представления задачи. Рассмотрим одно- или многопозиционную систему наблюдения, состоящую из радиолокационных станций, обеспечивающих измерение дальности «объект-станция» и пеленга на объект. Введём правую декартову систему координат xyz с осью z, направленной в зенит, осью y, направленной на Север и осью x, направленной на Восток. Пусть модель движения объекта в выбранной системе координат, отождествляемая далее с моделью движения точки в пространстве, имеет вид:
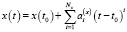 ,
,
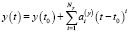 , (1)
, (1)
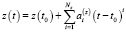 .
.
Здесь Nx, Ny, Nz – порядок полинома, применяемого при описании эволюции координат, 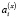 ,
, 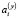 ,
, 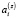 – полиномиальные коэффициенты, отождествляемые со скоростями объекта и приведёнными значениями старших производных.
– полиномиальные коэффициенты, отождествляемые со скоростями объекта и приведёнными значениями старших производных.
Информационная ситуация, обеспечиваемая системой из J РЛС, описывается следующей моделью измерений:
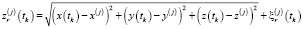 ,
,
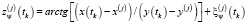 (2)
(2)
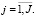
Здесь 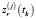 ,
, 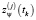 – показания дальности и азимута до объекта на j-й станции в момент времени tk;
– показания дальности и азимута до объекта на j-й станции в момент времени tk; 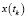 ,
, 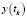 ,
, 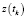 – отнесённые к этому времени координаты объекта;
– отнесённые к этому времени координаты объекта; 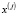 ,
, 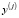 ,
, 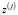 – координаты j-й станции;
– координаты j-й станции; 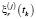 ,
, 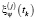 – случайные инструментальные погрешности измерений, причем
– случайные инструментальные погрешности измерений, причем
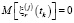 ,
,
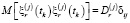 ,
,
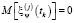 ,
,
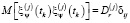 ,
,
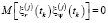 ,
,
δij – символ Кронекера.
В свете модельных представлений (1) и (2) может быть поставлена обратная задача, целью решения которой является определение вектора
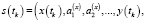
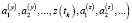
по измерениям параметров 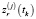 ,
, 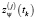 .
.
Допуская наличие опорного решения, характеризующего априорные представления о траектории объекта, будем говорить о сведении исходной задачи к задаче «в малом» с искомым вектором
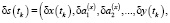
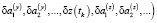 ,
,
характеризующем погрешности априорных представлений. Линеаризация приводит исходную задачу к следующему виду:
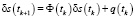 ,
,
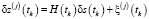 , (3)
, (3)
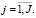
Здесь 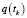 – вектор не моделируемых параметров движения,
– вектор не моделируемых параметров движения, 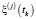 – вектор инструментальных погрешностей измерений,
– вектор инструментальных погрешностей измерений, 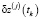 – вектор невязок измерений,
– вектор невязок измерений, 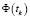 ,
, 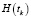 – матричные коэффициенты (матрицы частных производных), формируемые согласно равенствам:
– матричные коэффициенты (матрицы частных производных), формируемые согласно равенствам:
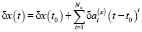 ,
,
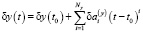 , (4)
, (4)
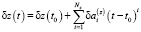
и 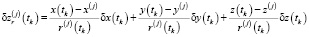
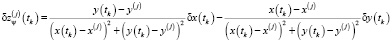 , (5)
, (5)
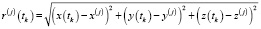 ,
, 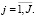
Для исследования принципиальной разрешимости (наблюдаемости) задачи (3) сведём её к конечномерному виду и проанализируем матрицу соответствующей системы алгебраических линейных уравнений на предмет вырожденности. Рассмотрим некоторый временной интервал наблюдения [t1, tm], за который произведены измерения. Запишем систему уравнений (5) с учётом решения уравнений эволюции погрешностей (4) при начальных условиях s(t*), особо отмечая при этом, что момент времени t* может как принадлежать интервалу наблюдения, так и находится вне его. Таким образом, будем иметь следующую систему уравнений измерений:
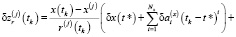
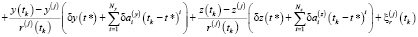
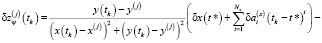
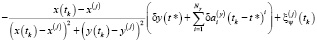 (6)
(6)
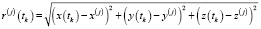 ,
,
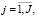
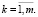
Последняя система может быть записана компактно в виде
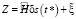 .
.
В общем случае, в силу линейной независимости системы функций, образующих матрицу системы (6), можно говорить о полноте ранга этой матрицы, а значит, и о возможности наблюдения полного вектора 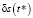 . Вместе с тем, следует особо отметить и существование запрещённых (ненаблюдаемых) решений задачи (1), (2), а следовательно, и опорных решений задачи (4), (5), приводящих соответствующую матрицу
. Вместе с тем, следует особо отметить и существование запрещённых (ненаблюдаемых) решений задачи (1), (2), а следовательно, и опорных решений задачи (4), (5), приводящих соответствующую матрицу 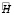 к вырождению. Проводя её аналитическое исследование, можно выделить несколько классов таких ненаблюдаемых решений.
к вырождению. Проводя её аналитическое исследование, можно выделить несколько классов таких ненаблюдаемых решений.
Ненаблюдаемые опорные траектории задачи
Утверждение 1. Если количество станций J = 1, а опорное решение в задаче (4), (5) такое, что 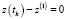 (то есть траектория движения объекта полностью лежит в плоскости вращения антенны РЛС), то соответствующая системе (6) матрица
(то есть траектория движения объекта полностью лежит в плоскости вращения антенны РЛС), то соответствующая системе (6) матрица 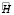 вырождена.
вырождена.
Доказательство. Рассмотрим систему уравнений (6). В условиях однопозиционного наблюдения при 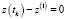 коэффициенты при величинах
коэффициенты при величинах 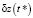 и
и 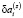 всегда будут равны нулю, что, с учетом вида второго уравнения системы (6), означает наличие нулевых столбцов в матрице
всегда будут равны нулю, что, с учетом вида второго уравнения системы (6), означает наличие нулевых столбцов в матрице 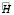 . Такая матрица, очевидно, вырождена.
. Такая матрица, очевидно, вырождена.
Утверждение 2. Если количество станций J = 1, а опорное решение в задаче (4), (5) такое, что 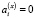 ,
, 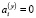 ,
, 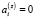 (объект покоится), то соответствующая системе (6) матрица
(объект покоится), то соответствующая системе (6) матрица 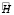 вырождена.
вырождена.
Доказательство. Рассмотрим систему уравнений (6). При 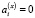 ,
, 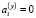 ,
, 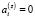 имеют место равенства:
имеют место равенства: 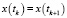 ,
, 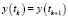 ,
, 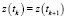 , что в условиях однопозиционного наблюдения означает линейную зависимость строк соответствующей матрицы
, что в условиях однопозиционного наблюдения означает линейную зависимость строк соответствующей матрицы 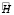 , то есть матрица
, то есть матрица 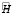 вырождена.
вырождена.
Утверждение 3. Если количество станций J = 1, а опорное решение в задаче (4), (5) такое, что 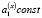 ,
, 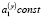 ,
, 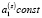 , Nz > 0 (объект движется по прямой, и вертикальная скорость входит в число оцениваемых параметров), то соответствующая системе (6) матрица
, Nz > 0 (объект движется по прямой, и вертикальная скорость входит в число оцениваемых параметров), то соответствующая системе (6) матрица 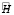 вырождена.
вырождена.
Доказательство. Рассмотрим систему уравнений (6). Не теряя общности, рассмотрим задачу (4), (5) при Nx = 1, Ny = 1, Nz = 1. При таком составе искомых переменных в случае однопозиционного наблюдения система уравнений (6) имеет вид:
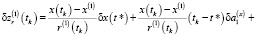
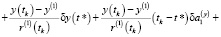
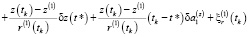 ,
,
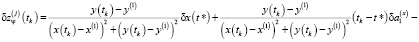
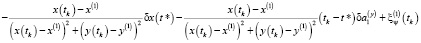 ,
,
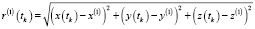 ,
, 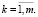
С учётом изучаемых свойств движения имеют место дополнительные условия:
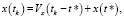
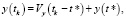
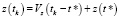
при константных значениях скоростей Vx, Vy, Vz.
Для того, чтобы показать вырожденность соответствующей матрицы  , докажем линейную зависимость её столбцов в указанных условиях (их количество – 6 в данном случае).
, докажем линейную зависимость её столбцов в указанных условиях (их количество – 6 в данном случае).
Если столбцы матрицы 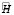 линейно зависимые, то существуют такие 6 чисел A, B, C, D, E, F не равные одновременно нулю, что имеют место равенства (не теряя общности, для простоты будем считать, что x(1) = 0, y(1) = 0, z(1) = 0, t* = 0):
линейно зависимые, то существуют такие 6 чисел A, B, C, D, E, F не равные одновременно нулю, что имеют место равенства (не теряя общности, для простоты будем считать, что x(1) = 0, y(1) = 0, z(1) = 0, t* = 0):
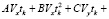
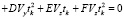 , (7)
, (7)
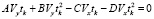 .
.
Чтобы эти два равенства были верны для любых tk, необходимо и достаточно одновременное выполнение следующих условий:
BVx + DVy + FVz = 0,
AVx + CVy + EVz = 0,
BVy – DVx = 0,
AVy – CVx = 0.
Очевидно, что этим условиям могут удовлетворить бесконечное множество значений A, B, C, D, E, F. Таким образом, при заданных свойствах наблюдения и движения существует континуальное множество шестёрок чисел A, B, C, D, E, F, обращающих (7) в верное равенство (то есть линейная комбинация столбцов соответствующей матрицы 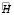 обращается в 0), а значит, соответствующая матрица
обращается в 0), а значит, соответствующая матрица 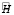 вырождена.
вырождена.
Аналогичным путём (правда, несколько усложнив выражения) можно показать вырожденность 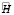 и при x(1) ≠ 0, y(1) ≠ 0, z(1) ≠ 0, t* ≠ 0. При более высоких размерностях задачи
и при x(1) ≠ 0, y(1) ≠ 0, z(1) ≠ 0, t* ≠ 0. При более высоких размерностях задачи 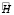 будет также, очевидно, вырождена, так как у неё будут линейно зависимы уже рассмотренные 6 столбцов.
будет также, очевидно, вырождена, так как у неё будут линейно зависимы уже рассмотренные 6 столбцов.
Утверждение 4. Если количество станций J = 1, а опорное решение в задаче (4), (5) такое, что 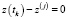 для всех j (все станции расположены на одной высоте и траектория объекта полностью лежит в плоскости вращения их антенн), то соответствующая системе (6) матрица
для всех j (все станции расположены на одной высоте и траектория объекта полностью лежит в плоскости вращения их антенн), то соответствующая системе (6) матрица 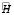 – вырождена.
– вырождена.
Доказательство. Рассмотрим систему уравнений (6). При указанной конфигурации системы при 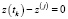 коэффициенты при величинах
коэффициенты при величинах 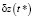 и
и 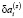 всегда будут равны нулю, что, с учётом вида второго уравнения системы (6), означает наличие нулевых столбцов в соответствующей матрице
всегда будут равны нулю, что, с учётом вида второго уравнения системы (6), означает наличие нулевых столбцов в соответствующей матрице 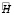 . Такая матрица, очевидно, вырождена.
. Такая матрица, очевидно, вырождена.
Несмотря на рассмотренные ограничения, система (6) остаётся невырожденной для достаточно широкого класса решений (траекторий), характерных для реальных ситуаций (например, при движениях объекта в рамках модели (1) вне плоскости вращения антенн). Исходя из этого, можно сделать вывод, что постановка задачи наблюдения в виде (1), (2) правомерна с точки зрения её принципиальной разрешимости.
Отмеченная сингулярность построенной модели вблизи точки 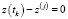 , приводящая к обнулению соответствующего коэффициента в первом уравнении системы (6), отвечающего за определение координаты z наблюдаемого объекта, способна существенно ограничить эффективность моделей такого типа, особенно в области малых отношений «высота/дальность». Определённые перспективы в этом направлении может дать переход в модели (1), (2) от прямоугольных координат к сферическим.
, приводящая к обнулению соответствующего коэффициента в первом уравнении системы (6), отвечающего за определение координаты z наблюдаемого объекта, способна существенно ограничить эффективность моделей такого типа, особенно в области малых отношений «высота/дальность». Определённые перспективы в этом направлении может дать переход в модели (1), (2) от прямоугольных координат к сферическим.
В целом приведённое исследование даёт возможность выбора того или иного типа модели решения пространственной задачи навигации в различных реальных ситуациях.
Библиографическая ссылка
Гриняк В.М., Герасименко Л.В. АНАЛИЗ РАЗРЕШИМОСТИ ЗАДАЧИ НАБЛЮДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ ДВУХКООРДИНАТНЫМИ ИЗМЕРИТЕЛЯМИ // Современные наукоемкие технологии. 2016. № 8-2. С. 214-219;URL: https://top-technologies.ru/ru/article/view?id=36131 (дата обращения: 22.02.2026).



