Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Вашкевич Н.П. 1 Сибиряков М.А. 2

---

1 Пензенский государственный университет

2 Поволжский государственный технологический университет

Правильная организация алгоритмического управления в любой вычислительной системе значительно влияет на ее производительность, эффективность управления процессами и ресурсами. При разработке таких систем актуальна задача формализации алгоритмов обработки и управления. Особое внимание в данной статье уделяется математическому аппарату, связанному с формальным представлением алгоритмов в виде модели конечных автоматов. В качестве основной модели конечного автомата принята система рекуррентных канонических уравнений (СКУ), описывающих все реализуемые в системе частные события, принят язык граф-схем алгоритмов. Основной целью статьи является формализация рассматриваемых алгоритмов обработки кэшируемых данных в системах хранения данных с помощью СКУ. В статье представлены граф-схемы алгоритмов, на основе которых составлены системы канонических уравнений. Полученное математическое представление является, по существу, исполнимой формализованной спецификацией, которая позволяет осуществить непосредственный переход от СКУ к программной или аппаратной реализации данных алгоритмов.

Статья в формате PDF

0 KB

системы хранения данных

обработка и хранение данных

кэширование

формализация алгоритмов

конечные автоматы

система канонических уравнений

1. Вашкевич Н.П. Выразительные возможности и эффективность формального языка, построенного на основе использования моделей недетерминированных автоматов // Известия высших учебных заведений. Поволжский регион. Технические науки. – 2006. – № 6. – С. 67–77.

2. Вашкевич Н.П., Зубков В.А. Алгоритм синтеза цифровых автоматов Мура с использованием языка исчисления предикатов // Вычислительная техника: Учебные записки. – Вып. 3. Пенза: Пенз. политехн. ин-т, 1969 – С. 25–36.

3. Вашкевич Н.П. Об одном способе синтеза цифровых автоматов по граф-схеме алгоритма с параллельными ветвями // Вычислительная техника: Межвуз. сб. науч. тр., Вып. 1, 2. – Пенза: Пенз. политехн. ин-т, 1973.

4. Вашкевич Н.П., Бикташев Р.А. Достоинство формального языка, основанного на концепции недетерминизма, при структурной реализации параллельных систем логического управления процессами и ресурсами // Известия высших учебных заведений. Поволжский регион. Технические науки. – 2011. – № 1 (7). – С. 3–11.

5. Sibiryakov M.A., Vasyaeva E.S., Koshpaev A.A. Analysis and comparison of cache memory control methods in storage systems // In the World Scientific. Ser.: Natural Technical Sciences. – Krasnoyarsk, 2014. – № 10 (58). – P. 276–280.

Для обеспечения обработки и хранения большого объема информации в современных сетевых инфраструктурах применяются системы хранения данных (СХД). Одним из способов повышения производительности СХД является использование кэширования. Производительность применяемой в таких системах кэш-памяти во многом определяется эффективностью реализуемых алгоритмов обработки кэшируемых данных. При разработке таких алгоритмов актуальной задачей является их формальное представление. Одним из способов формального описания алгоритмов является применение математического аппарата, связанного с их представлением на основе модели конечных автоматов с использованием рекуррентных бескванторных предикатных уравнений или систем канонических уравнений, предложенных Н.П. Вашкевичем для последовательных [1, 2] и параллельных [3, 4] алгоритмов.

Системы канонических уравнений для алгоритмов обработки кэшируемых данных

Формализуем граф-схемы алгоритмов обработки кэшируемых данных (обработки команды чтения и вытеснения данных в кэш-памяти) с помощью систем канонических уравнений. СКУ позволяет формировать компактные представления алгоритмов с описанием функций переходов в терминах частных событий. Данные события реализуются в частичных детерминированных автоматах Мура, в которых соблюдаются условия однозначности переходов, то есть под воздействием одного частичного входного сигнала или комбинации таких сигналов возможен переход от некоторого исходного события только к одному событию.

На рис. 1 и 2 представлены блок-схемы алгоритмов обработки кэшируемых данных, разработанных в рамках модификации метода обработки кэшируемых данных с использованием индексных таблиц [5]. Для них разработаны укрупненные граф-схемы алгоритмов (ГСА, рис. 3 и 4), на основе которых построены СКУ. Результаты укрупнения представлены в табл. 1 и 2. В данных ГСА следующие подряд условные вершины разделены операторными вершинами – разделительными событиями, которые подразумевают ожидание. Они введены для упрощения и корректной реализации СКУ. Операторы ГСА требуют различных времен выполнения, поэтому каждое уравнение СКУ построено не только при учете условий зарождения, но и при учете условия сохранения события.

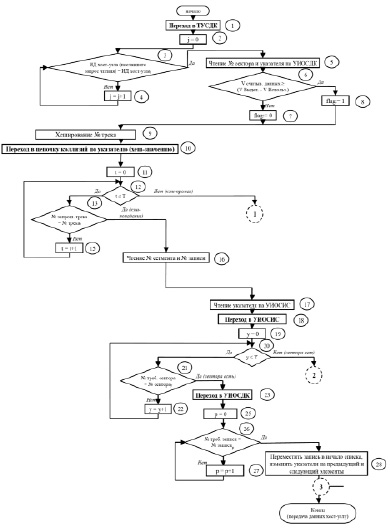
Рис. 1. Блок-схема модифицированного алгоритма обработки команды чтения данных

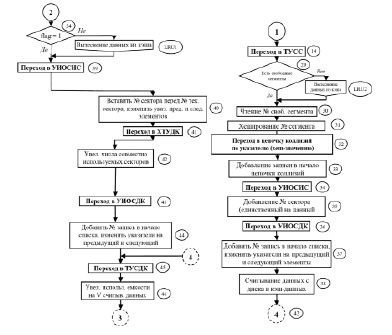
Продолжение рис. 1

Таблица 1

Вершины модифицированного алгоритма вытеснения данных, составляющие операторы укрупненных ГСА

Примечание. События S3, S4 – разделительные.

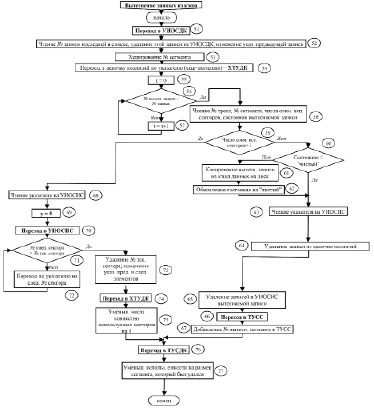
Рис. 2. Блок-схема модифицированного алгоритма вытеснения чтения

СКУ1 для ГСА1:

S0(t + 1) = S0(t)&¬x0(t) ∨ xbegin(t);

S1(t + 1) = S0(t)& x0(t) ∨ S1(t)&¬z1(t);

S2(t + 1) = S1(t)&z1(t)&x1(t) ∨ S2(t)&z2(t)&x1(t) ∨ S2(t)&¬z2(t);

S3(t + 1) = S1(t)&z1(t)&¬x1(t) ∨ S2(t)&z2 (t)&¬x1(t) ∨ S3(t)&¬z3(t);

S4(t + 1) = S3(t)&z3(t)&x2(t) ∨ S4(t)&¬z4(t);

S5(t + 1) = S4(t)&z4(t)&x3(t) ∨ S5(t)&¬z5(t);

S6(t + 1) = S4(t)&z4(t)&¬x3(t) ∨ S6(t)&¬z6(t);

S7(t + 1) = S5(t)&z5(t) ∨ S6(t)&z6(t) ∨ S7(t)&¬z7(t);

S8(t + 1) = S3(t)&z3(t)¬x2(t) ∨ S8(t)&¬z8(t);

S9(t + 1) = S8(t)&z8(t)&x4(t) ∨ S9(t)&z9(t)&x4(t) ∨ S9(t)&¬z9(t);

S10(t + 1) = S8(t)&z8(t)&¬x4(t) ∨ S9(t)&z9(t)&¬x4(t) ∨ S10(t)&¬z10(t);

S11(t + 1) = S10(t)&z10(t) ∨ S7(t)&z7(t) ∨ S11(t)&¬z11(t);

Sk(t + 1) = S11(t)&z11(t) ∨ Sk(t)&¬zk(t),

где Si(t) – унарный предикат, определенный на множестве значений дискретного времени t. Истинность Si(t) означает, что автомат находится в состоянии Si в момент времени t, или в автомате реализуется частное событие Si в момент времени t. Входные сигналы xj(t) – частичные, т.е. на переход влияет сам сигнал, а не комбинация всех сигналов, как в случае полного автомата; xbegin(t) – сигнал установки автомата в начальное состояние. Входные сигналы xj(t) представлены унарными предикатами.

Исходя из того, что времена работы операторов различные, необходимо учесть условия окончания работы операторов, то есть каждый оператор по окончании своей работы должен выдать сигнал окончания. Тогда примем, что zi(t) – условие сохранения события Si при zi(t) = 0 («false»); при zi(t) = 1 («true») событие Si не сохраняется и происходит переход к следующему событию. Сигнал, или условие zi(t), формируется при выполнении события Si (условие zi(t) может быть истинным только после выполнения события Si). Использование условия сохранения позволяет событию Si выполняться за необходимое количество тактов.

Используемый в работе алгоритмов индекс включает в себя шесть базовых индексных таблиц [4]: ХТУДК – хеш-таблица управления; ТУСС – таблица управления свободными сегментами; УИОСДК – таблица, хранящая управляющую информацию о секторах дискового кэша; УИОСИС – таблица, содержащая управляющую информацию о совместно используемых сегментах; ТУСДК – таблица управления секторами дискового кэша.

Таблица 2

Вершины модифицированного алгоритма обработки команды чтения данных, составляющие операторы укрупненных ГСА

Примечание. События S4, S5, S8, S9 – разделительные.

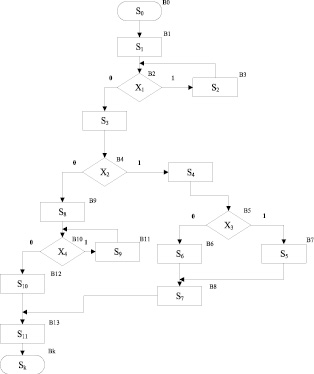
Рис. 3. Граф-схема модифицированного алгоритма вытеснения данных (ГСА1)

СКУ2 для ГСА2:

S0(t + 1) = S0(t)&¬x0(t) ∨ xbegin(t);

S1(t + 1) = S0(t)&x0(t) ∨ S1(t)&¬z1(t);

S2(t + 1) = S1(t)&z1(t)&x1(t) ∨ S2(t)&z2(t)&x1(t) ∨ S2(t)&¬z2(t);

S3(t + 1) = S1(t)&z1(t)&¬x1(t) ∨ S2(t)&z2(t)&¬x1(t) ∨ S3(t)&¬z3(t);

S4(t + 1) = S3(t)&z3(t)&x2(t) ∨ S6(t)&z6(t)&x2(t) ∨ S4(t)&¬z4(t);

S5(t + 1) = S3(t)&z3(t)&¬x2(t) ∨ S6(t)&z6(t)&¬x2(t) ∨ S5(t)&¬z5(t);

S6(t + 1) = S5(t)&z5(t)&x5(t) ∨ S6(t)&¬z6(t);

S7(t + 1) = S5(t)&z5(t)&¬x5(t) ∨ S7(t)&¬z7(t);

S8(t + 1) = S7(t)&z7(t)&x6(t) ∨ S10(t)&z10(t)&x6(t) ∨ S8(t)&¬z8(t);

S9(t + 1) = S7(t)&z7(t)&¬x6(t) ∨ S10(t)&z10(t)&¬x6(t) ∨ S9(t)&¬z9(t);

S10(t + 1) = S9(t)&z9(t)&x7(t) ∨ S10(t)&¬z10(t);

S11(t + 1) = S9(t)&z9(t)&¬x7(t) ∨ S11(t)&¬z11(t);

S12(t + 1) = S11(t)&z11(t)&x8(t) ∨ S12(t)&z12(t)&x8(t) ∨ S12(t)&¬z12(t);

S13(t + 1) = S11(t)&z11(t)&¬x8(t) ∨ S12(t)&z12(t)&¬x8(t) ∨ S13(t)&¬z13(t);

S14(t + 1) = S4(t)&z4(t)&x3(t) ∨ S14(t)&¬z14(t);

S15(t + 1) = S4(t)&z4(t)&¬x3(t) ∨ S14(t)&z14(t) ∨ S15(t)&¬z15(t);

S16(t + 1) = S15(t)&z15(t) ∨ S16(t)&¬z16(t);

S17(t + 1) = S8(t)&z8(t)&x4(t) ∨ S17(t)&¬z17(t);

S18(t + 1) = S17(t)&z17(t) ∨ S8(t)&z8(t)&¬x4(t) ∨ S18(t)&¬z18(t);

S19(t + 1) = S16(t)&z16(t) ∨ S18(t)&z18(t) ∨ S19(t)&¬z19(t);

Sk(t + 1) = S13(t)&z13(t) ∨ S19(t)&z19(t) ∨ Sk(t)&¬zk(t).

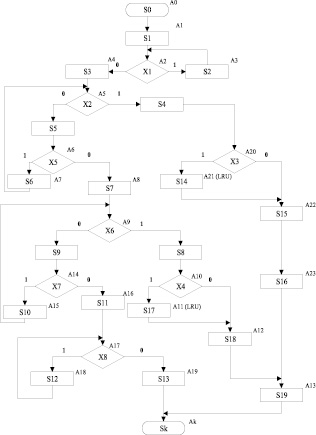
Рис. 4. Граф-схема алгоритма обработки команды чтения данных (ГСА2)

Система канонических уравнений для параллельного алгоритма обращения к индексным таблицам

Аналогичным образом представлена граф-схема разработанного параллельного алгоритма обращения к индексным таблицам (рис. 5), применяемого в рамках выполнения алгоритмов обработки кэшируемых данных. Приведена ее формализация с помощью СКУ.

СКУ3 для ГСА3:

S0(t + 1) = S0(t)&¬x0(t) ∨ xbegin(t);

S1(t + 1) = S0(t)&x0(t) ∨ S1(t)&¬z1(t);

S2(t + 1) = S0(t)&x0(t) ∨ S2(t)&¬z2(t);

S’1(t + 1) = S1(t)&z1(t) ∨ S’1(t)&¬(S3(t) ∨ S17(t));

S’2(t + 1) = S2(t)&z2(t) ∨ S’2(t)&¬( S3(t) ∨ S17(t));

S3(t + 1) = S’1(t)&S’2(t)&x1(t) ∨ S3(t)&¬z3(t);

S 4(t + 1) = S3(t)&z3(t)&x2(t)∨ S4(t)&¬z4(t);

S5(t + 1) = S3(t)&z3(t)&¬x2(t) ∨ S5(t)&¬z5(t);

S6(t + 1) = S5(t)&z5(t)&¬x3(t) ∨ S6(t)&¬z6(t);

S 7(t + 1) = S6(t)&z6(t)∨ S7(t)&¬z7(t);

S8(t + 1) = S7(t)&z7(t)&¬x4(t) ∨ S8(t)&¬z8(t);

S9(t + 1) = S7(t)&z7(t)&¬x4(t) ∨ S9(t)&¬z9(t);

S10(t + 1) = S7(t)&z7(t)&x4(t) ∨ S10(t)&¬z10(t);

S11(t + 1) = S7(t)&z7(t)&x4(t) ∨ S11(t)&¬z11(t);

S’8(t + 1) = S8(t)&z8(t) ∨ S’8(t)&¬S12(t);

S’9(t + 1) = S9(t)&z9(t) ∨ S’9(t)&¬S12(t);

S’10(t + 1) = S10(t)&z10(t) ∨ S’10(t)&¬S12(t);

S’11(t + 1) = S11(t)&z11(t) ∨ S’11(t)&¬S12(t);

S12(t + 1) = S’8(t)&S’9(t)&S’10(t)&S’11(t) ∨ S12(t)&¬z12(t);

S13(t + 1) = S12(t)&z12(t)∨S5(t)&x3∨ S13(t)&¬z13(t);

S14(t + 1) = S12(t)&z12(t)∨S5(t)&x3∨ S14(t)&¬z14(t);

S15(t + 1) = S12(t)&z12(t)∨S5(t)&x3∨ S15(t)&¬z15(t);

S16(t + 1) = S12(t)&z12(t)∨S5(t)&x3∨ S16(t)&¬z16(t);

S’13(t + 1) = S13(t)&z13(t)∨ S’13(t)&¬Sk(t);

S’14(t + 1) = S14(t)&z14(t)∨ S’14(t)&¬Sk(t);

S’15(t + 1) = S15(t)&z15(t)∨ S’15(t)&¬Sk(t);

S’16(t + 1) = S16(t)&z16(t)∨ S’16(t)&¬Sk(t);

S17(t + 1) = S’1(t)&S’2(t)&¬x1(t) ∨ S17(t)&¬z17(t);

S18(t + 1) = S17(t)&z17(t)&¬x5(t) ∨ S18(t)&¬z18(t);

S19(t + 1) = S18(t)&z18(t)& ∨ S19(t)&¬z19(t);

S20(t + 1) = S18(t)&z18(t)& ∨ S20(t)&¬z20(t);

S21(t + 1) = S18(t)&z18(t)&∨ S21(t)&¬z21(t);

S’19(t + 1) = S19(t)&z19(t) ∨ S’19(t)&¬S22(t);

S’20(t + 1) = S20(t)&z20(t) ∨ S’20(t)&¬S22(t);

S’21(t + 1) = S21(t)&z21(t) ∨ S’21(t)&¬S22(t);

S22(t + 1) = S’19(t)&S’20(t)&S’21(t)∨ S17(t)&x5∨ S’22(t)¬z22(t);

S23(t + 1) = S22(t)&z22(t)∨ S23(t)&¬z23(t);

S24(t + 1) = S23(t)&z23(t)∨ S24(t)&¬z24(t);

S25(t + 1) = S23(t)&z23(t)∨ S25(t)&¬z25(t);

S26(t + 1) = S23(t)&z23(t)∨ S26(t)&¬z26(t);

S27(t + 1) = S23(t)&z23(t)∨ S27(t)&¬z27(t);

S’24(t + 1) = S24(t)&z24(t) ∨ S’24(t)&¬Sk(t);

S’25(t + 1) = S25(t)&z25(t) ∨ S’25(t)&¬Sk(t);

S’26(t + 1) = S26(t)&z26(t) ∨ S’26(t)&¬Sk(t);

S’27(t + 1) = S27(t)&z27(t) ∨ S’27(t)&¬Sk(t);

Sk(t + 1) = S4(t)&z4(t) ∨ S’13(t)&S’14(t)&S’15(t)&S’16(t)∨ S’24(t)&S’25(t)&S’26(t)&S’27(t)∨ Sk(t)&¬zk(t).

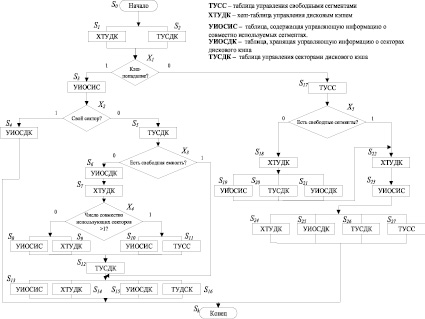
Рис. 5. Граф-схема параллельного алгоритма обращения к индексным таблицам (ГСА3)

Аналогично предыдущим случаям в СКУ3 учтены условия сохранения событий. Для параллельных событий (S8, S9; S10, S11; S13 – S16; S19 – S21; S24 – S27) принято, что факт завершения каждого Si-го события отмечается последующим появлением события Si’. Например, для подтверждения фактов завершения событий S1 и S2 определены события S1’ и S2’. С того момента t, как только высказывания S1’(t) и S2’(t) одновременно станут истинными («true»), в зависимости от значения входного символа x1 появится одно из событий S3 или S17, которое в следующем такте «прекратит» выполнение событий S1’ и S2’.

Выводы

Таким образом, построены системы канонических уравнений для алгоритмов обработки кэшируемых данных в системе хранения данных. Такая математическая модель является, по существу, исполнимой формализованной спецификацией. Она позволяет осуществить непосредственный переход от СКУ к программной или аппаратной реализации данных алгоритмов.

Библиографическая ссылка