Расчет валов на жесткость необходим для оценки работоспособности самых различных механизмов. Например, кинематическая точность приводов следящих систем существенно зависит от крутильной жесткости основных элементов [10]. От жесткости вала и точности расчета угла закручивания зависит эффективность работы делительных механизмов [2]. Расчет валов на жесткость необходим для предотвращения резонансных колебаний [3]. Так, широко известно, что по причине колебаний произошло крушение «Цеппелина» при попытке перелета через Атлантический океан [1].
Традиционный расчет вала на жесткость при кручении сводится к следующей процедуре. Вал разбивается на грузовые участки, строится эпюра крутящих моментов, определяются углы закручивания, строится эпюра углов закручивания, указывается положение образующей [11]. Расчет этих валов на жесткость обычно сопровождается построением эпюры углов поворота поперечных сечений, при этом если имеется жесткая заделка, то именно она и является началом отсчета. Если вал расположен в подшипниках, то в литературе отсутствует определенность: рекомендуется выбор различных точек начала отсчета. Так, одни авторы в качестве начала координат рекомендуют использовать крайнее левое сечение и правило внешней нормали как правило знаков [11]. Другие за начало отсчета рекомендуют принимать сечение, проходящее через ведущий шкив, и при построении эпюры углов поворота двигаться к этому сечению с двух разных концов [9]. Вместе с тем, от выбора точки отсчета зависит расчетная длина участка вала, влияющая на значение угла закручивания и, соответственно, на расчетное значение крутильной жесткости вала.
Точность определения фактической жесткости вала, при условии, что допускаемый угол закручивания на метр длины измеряется в минутах и секундах, может привести к нарушению работоспособности агрегата, поскольку, например, при его пуске или остановке, при больших моментах инерции и скоростях вращения, вероятно возникновение недопустимых динамических нагрузок. Варьирование крутильной жесткости валов позволяет снизить динамические нагрузки на 20–30 % [8]. Учет сил инерции требует сложных методов расчета [5], поэтому в их основе должны быть соответствующие исходные данные. Таким образом, расчет валов при кручении является актуальной задачей.
При расчете крутильных колебаний валов в качестве узлов колебаний принимаются неподвижные сечения, и длина грузового участка определяется расстоянием между этими узлами. Мерой инертности отдельного звена является момент инерции, а период собственных колебаний определяется длиной участка, жесткостью вала и моментом инерции маховика.
Ниже также предлагается в качестве границ грузовых участков принимать неподвижные сечения. Аналогом неподвижных сечений при растяжении-сжатии может служить срединное сечение эспандера (рис. 1). Жесткость вала на отдельных участках следует оценивать по углу закручивания. Это актуально, в частности, при расчете коэффициента концентрации нагрузки валов-шестерен, шлицевых соединений и в других случаях. Например, если при расчете шестерни за начало отсчета принимать край и середину, то очевидно, что в одном случае ввиду ограниченной точности изготовления нагрузка сконцентрируется по одному краю (рис. 2), а в другом будет распределена более равномерно. Для оценки коэффициента распределения нагрузки существуют различные методы расчета [6], однако ряд авторов при расчете и шлицевых [7] и шпоночных [4] соединений стремится к упрощенным решениям.
Рис. 1. Растяжение эспандера
На рис. 3, а представлена расчетная схема вала, расположенного на двух подшипниках. На валу жесткостью GIP имеются ведущий и два ведомых шкива, передающих крутящие моменты Т0, Т1, Т2.
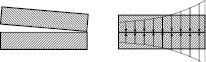
Рис. 2. Характер распределения нагрузки
Требуется определить положение непо-движных сечений, построить эпюры углов поворота и указать положение образующей.
Для определения положения неподвижных сечений предлагается разбить вал на участки, расположенные между крутящими моментами и определить угол закручивания, а следовательно, и положение образующей на каждом отдельном участке.
На рис. 3, б представлена эпюра крутящих моментов, позволяющая разделить вал на левую и правую части (рис. 3, в г). Очевидно, что в силу симметрии неподвижными сечениями этих частей будут сечения 3 и 4. При этом образующие этих частей примут положения, изображенные на рисунках 3в и 3г. Эпюры углов поворота сечений левой и правой частей представлены сплошными линиями на рисунке 3д. Поскольку вал представляет собой единое целое, левая и правая части должны повернуться навстречу друг другу вместе с сечениями 3 и 4 таким образом, чтобы эпюра углов поворота была непрерывна. Уместно предположить, что для участков вала постоянной жесткости и равной длины мерой деформационной инертности является крутящий момент, поэтому с учетом эпюры крутящих моментов угол поворота левой части вдвое превысит правый, и окончательная эпюра углов поворота примет вид штриховой линии на рис. 3, д. Далее легко графически определить положение неподвижных сечений 5 и 6 (рис. 3, д) и показать окончательное положение образующей (рис. 3, е). При оценке углов поворота поперечных сечений принимается следующая нумерация (рис. 3, в, г):
0 – центральное сечение вала;
1 и 2 – крайние левое и правое сечение вала;
3 и 4 – центральное сечение отдельно рассматриваемых левой и правой частей;
5 и 6 – неподвижные сечения левой и правой части при рассмотрении вала как единого целого.
С учетом симметрии углы поворота сечений будут иметь следующие значения:
;
,
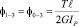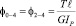a
,
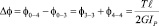где первый подстрочный индекс указывает номер сечения, которое поворачивается, а второй – номер сечения, относительно которого отсчитывается угол поворота.
В соответствии с предложенной гипотезой левая половина вала повернется навстречу правой на угол:
,
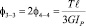следовательно, центральное сечение (сечение 0) всего вала повернется на угол 3-3 вместе с левой половиной и на угол 0-3 относительно середины левой части, т.е. на угол:
.
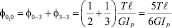Из подобия треугольников 5001, и 3002 следует, что отрезок 5 – 0 составляет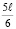 
, а величина 
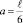(рис. 3, д). Аналогично из подобия треугольников 0340, и 0160 следует, что отрезок 0 – 6 составляет 
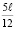, а величина 
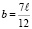(рис. 3, д). Окончательные положения неподвижных сечений 5 и 6, а также положение образующей представлены на рис. 1, е.
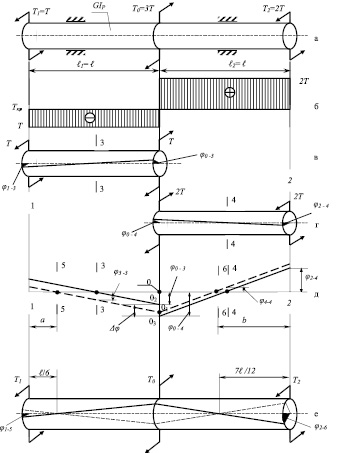
Рис. 3. К расчету на жесткость вала, закрепленного в двух подшипниках
Все представленные расчеты основаны на предложенной выше гипотезе, которая требует доказательств. Для доказательства предложенной гипотезы используется принцип минимума потенциальной энергии. Очевидно, что, так как под действием приложенных моментов Т0, Т1, Т2 вал находится в равновесии, вся энергия действующих крутящих моментов уходит в упругую деформацию. Поскольку при расчете валов действующие крутящие моменты известны, длины грузовых участков (расстояния между неподвижными сечениями) также определены, не составляет труда вычислить энергию, стремящуюся повернуть вал по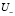 
и против 
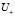часовой стрелки:
,
.
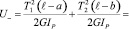
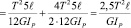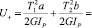
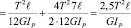Условие равновесия выполняется, поэтому выдвинутое предположение считаем обоснованным, а сечения 5 и 6 неподвижными.
Очевидно, что в состоянии покоя (до приложения нагрузки) образующая имеет вид горизонтальной штрих-пунктирной линии (рис. 3, е). В рабочем режиме образующая принимает вид сплошной линии (рис. 3, е), а при торможении, что неизбежно, например, в случае реверса, образующая примет вид пунктирной линии, являющейся зеркальным отражением сплошной (рис. 3, е). При этом угол, на который повернется по инерции шкив Т2, составит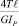 
, если за начало отсчета принять сечение 0. Если за начало отсчета принять сечение 6, то этот угол составит значительно меньшую величину 
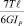. Для других шкивов углы поворота, а следовательно, и величины сил инерции, возникающие при пуске и остановке, также будут существенно зависеть от выбора начала отсчета.
Основным результатом выполненной работы является методика определения неподвижных сечений вала постоянной жесткости. Это позволяет уточнить расчет вала на крутильную жесткость, возникающие динамические нагрузки, возможные концентрации напряжений. При расчете ступенчатых валов или валов переменной жесткости расчеты несколько усложняются, но принципиально ничего не изменяется. Следует также отметить, что прослеживается некоторая аналогия между неподвижными сечениями при кручении и нейтральной осью при изгибе.
Библиографическая ссылка
Кузьмин А.А., Павлова Э.А. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ НА ОСНОВЕ МЕТОДИКИ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЙ НЕПОДВИЖНЫХ СЕЧЕНИЙ // Современные наукоемкие технологии. – 2016. – № 8-1. – С. 64-67;URL: https://top-technologies.ru/ru/article/view?id=36103 (дата обращения: 21.11.2024).