Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кобрунов А.И. 1 Мотрюк Е.Н. 1 Кунцев В.Е. 1

---

1 ФГБОУ ВО «Ухтинский государственный технический университет»

Разработан алгоритм расчета траектории движения особой точки восстановления давления как кратчайшего пути между парами скважин. На его основе рассчитываются интервальные времена наступления реакции в каждой из принимающих скважин на изменение режима давления в остальных, рассматриваемых по отдельности. Этим обеспечивается решение прямой задачи расчета траекторий движения особой точки для заданного распределения пьезопроводности для реализации алгоритма гидродинамической томографии. Траектория движения рассматривается как обеспечивающая минимальное время движения особой точки со скоростью, зависящей от длины пройденного пути. Решение основано на принципе оптимальности Беллмана. Создана программная реализация алгоритма, и выполнены тестовые эксперименты, характеризующие качественную работу алгоритма. Алгоритм расчёта интервальных времен составляет компоненту вычислительной технологии гидродинамической томографии для нахождения пространственного распределения коэффициента пьезопроводности и фильтрационного сопротивления, характеризующего продуктивную способность проницаемого пласта.

Статья в формате PDF

0 KB

траектория особой точки

минимизация времени движения

принцип Беллмана

скважина

кратчайший путь

интервальные времена

гидродинамическая томография

коэффициент пьезопроводности

1. Вентцель Е.С. Исследование операций: задачи, принципы, методология. 2-е изд. – М.: Наука, 1988. – 208 с.

2. Ипатов А.И., Кременецкий М.И. Геофизический и гидродинамический контроль разработки месторождений углеводородов. – М.: Ижевск, 2010. – 780 с.

3. Кобрунов А.И. Математическая модель томографии на давлениях при контроле за разработкой нефтяных месторождений // Известия Коми научного центра Уро РАН. – 2012. – Выпуск 4(12). – С. 82-86.

4. Кобрунов А.И. Теоретические основы гидродинамической томографии // Геофизический журнал. – 2015. – № 2. – С. 29-38.

5. Токарев В.В. Методы оптимальных решений. Том 2. Многокритериальность. Динамика. Неопределенность. 2-е изд., испр. – М.: ФИЗМАТЛИТ, 2011. – 420 с., – ISBN 978-5-9221-1258-1.

При разработке, мониторинге и планировании эксплуатации месторождения возникает задача определения пространственного распределения коэффициента фильтрационного сопротивления (пьезопроводности) движению флюида, характеризующего пропускную способность продуктивного пласта [2]. Ее решение обеспечивает технология веерной гидродинамической томографии, которая состоит в обработке и анализе веерных измерений интервалов времени наступления реакции в скважинах-приемниках на изменение режима давления в скважинах-источниках [4]. Практическая реализация технологии гидродинамической томографии может быть основана на косвенных измерениях интервальных времен распространения характерных точек кривых восстановления давления по анализу истории разработки месторождения. Прогноз томографических данных реализуется вычислительным экспериментом над построенной математической моделью месторождения в рамках гипотезы о характере ее основных компонентов [3].

В данной работе представлен алгоритм решения прямой задачи гидродинамической томографии поиска кратчайшего пути между парами скважин модели месторождения на основе принципа Беллмана [1, 5]. Что обеспечивает решение обратной задачи, основанной на итеративной схеме последовательного уточнения [3].

Рассматривается область S, в пределах которой выполняются построения. Координата точки из этой области обозначается ξ. Область S покрыта сеткой, которой соответствуют пары индексов 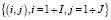так, что каждая точка области в сеточном представлении однозначно представима своими индексами 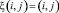. В области S задано стартовое распределение коэффициента пьезопроводности 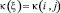. На сетке (рис. 1) расположены пары скважин 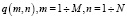, где m – номер скважины-источника возмущения и n – номер скважины-приемника возмущения. Всего пар скважин Q = M*N.

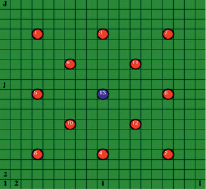
Рис. 1. Исходные данные для расчета оптимального пути

Распространение возмущения для каждой пары происходит по траекториям 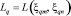, имеющим начало в точке 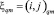и заканчивающимся в точке 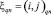. Траектории нумерованы индексом 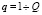, время движения возмущения по Lq есть q. Количество пройденных точек сетки в каждой траектории есть 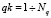. Текущая координата вдоль траектории Lq характеризуется переменной 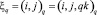. Время распространения движения волны q по Lq рассчитывается по формуле в дискретной форме:

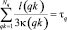, (1)

где l(qk) – длина части траектории Lq до ячейки qk. Наличие этого члена проявляется в снижении скорости по мере увеличения длины пути:

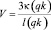. (2)

Траектория Lq, соединяющая точки ξm и ξn есть линия, служащая решением задачи:

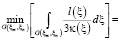
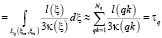, (3)

где G(ξm, ξn) – возможные траектории между парами скважин q(m, n).

В результате более длинный путь, обходящий зоны повышенных значений κ(qk), за счет снижения скорости по гиперболическому закону может оказаться проигрышным в сравнении с более коротким, проходящим через локальные максимумы κ(qk). Это специфика динамики распространения особой точки коэффициента пьезопроводности.

Алгоритм построения траектории Lq(m, n), вдоль которой будут определены значения l(qk), основан на последовательном нахождении окончания траектории начиная с текущего индекса zkq для траектории q до qn вместе с «остатком траектории» 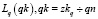в предположении, что 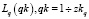, и, следовательно, l(qk) заданы своими нулевыми приближениями:

.

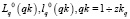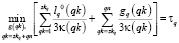, (4)

где gq(qk) – подобранные длины второй половины траектории для .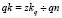

Алгоритм расчета основан на последовательном решении и сравнении результатов решения задачи, начиная от 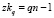до 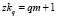. При этом для каждого qk сохраняются для последующего сравнения все значения конца траектории gq(zkq), служащие именем завершающего участка .

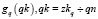После завершения счета найденная траектория Gq(qk), характеризующаяся длинами gq(qk), принимается за 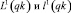соответственно.

Рассмотрим скважины с координатами (im, jm) и (in, jn). Согласно принципу Беллмана, движение при расчете траекторий начинается с принимающей скважины, т.е. с точки ξn = ξ(in, jn) и заканчивается в ξm = ξ(im, jm)

Шаг 1 (рис. 2, А). На первом шаге zkq = qn – 1 ищем J путей 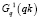из ξn = ξ(in, jn) в ячейки 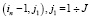и столько же путей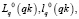 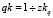из (im, jm) в (in – 1, j1).

Получаем пути для первого шага:

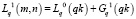(5)

и соответствующие им длины:

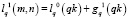. (6)

Шаг 2 (рис. 2, Б). На этом шаге zkq = qn – 2. Далее из ξn = ξ(in, jn) ищем пути 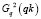в ячейки (in – 2, j2), через ячейки, для которых были найдены пути на шаге 1 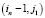, 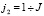. И столько же путей из (im, jm) в (in – 2, j2). На рис. 2, Б показан путь для одной из J ячеек.

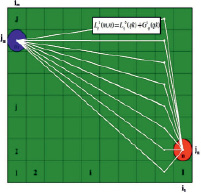
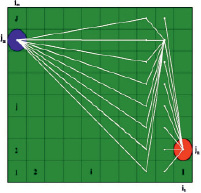
А Б

Рис. 2. А – Шаг 1; Б – Шаг 2

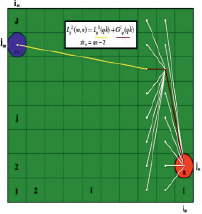
Шаг 3 (рис. 3, А). Получаем оптимальные траектории 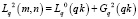и длины 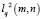, рассчитанные согласно условию, представленному в формуле (4). На рис. 3, А показан найденный путь, проходящий через ячейку (in – 2, j2), из ячейки ξn = ξ(in, jn) в ячейку (im, jm). Пути 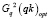запоминаем, далее работаем с ними.

Шаг 4. Если in – 2 im и j2 / jm, перейти к шагу 5. В противном случае перейти к шагу 8.

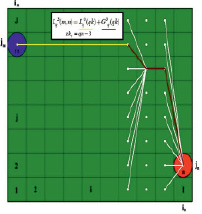
Шаг 5 (рис. 3, Б). Допустим, мы уже на итерации zkq = qn – z. Далее из n = (in, jn) ищем пути 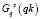в ячейки 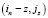, через ячейки, для которых были найдены пути на z – 1 шаге 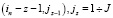. И столько же путей из (im, jm) в (in – z, jz).

Шаг 6 (рис. 3, Б). C учетом формулы (4), как условия оптимальности пути, находим 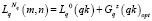и длины 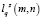. На рис. 3, Б показан путь для одной из J ячеек при z = 3.

Шаг 7. Если in – z / im и jz / jm, перейти к шагу 5. В противном случае перейти к шагу 8.

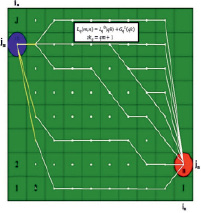
Шаг 8 (рис. 3, В). На последней итерации zkq = qm + 1 рассчитываем J значений 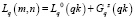. Далее находим минимальное по jz значение интервального времени распространения возмущения между скважинами, расположенными в точках n = (in, jn) и m = (im, jm), соответствующее значению индекса jz.

А Б

В

Рис. 3. А – Шаг 3; Б – Шаг 5 для z – 3; В – Шаг 8

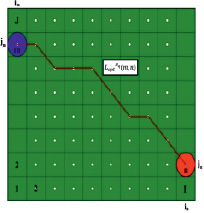
Оптимальная траектория, удовлетворяющая (4) и соединяющая точки (in, jn) и (im, jm), есть

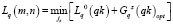. (7)

Программная реализация данного алгоритма была выполнена на языке Си#.

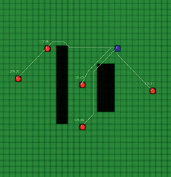
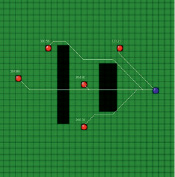
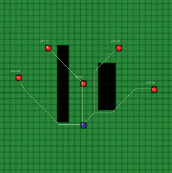
Тестовый пример. Рассмотрим модель, состоящую из 6 скважин (30 пар скважин), расположенных на однородной сети с двумя зонами повышенного фильтрационного сопротивления. На рис. 4 показаны кратчайшие пути из одной скважины к остальным, а также соответствующие этим путям интервальные времена.

А Б

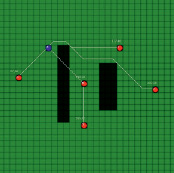
В Г

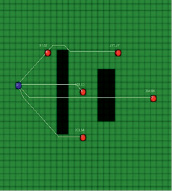
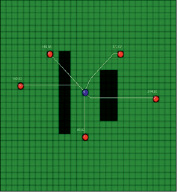
Д Е

Рис. 4. Результаты работы алгоритма: А – скважина-источник № 1; Б – скважина-источник № 2; В – скважина-источник № 3, Г – скважина-источник № 4, Д – скважина-источник № 5, Е – скважина-источник № 6

Получены ожидаемые результаты (пути и времена), что свидетельствует о корректной и эффективной работе алгоритма.

Таким образом, разработанный алгоритм и программа могут быть использованы для получения интервальных времен, обеспечивающих алгоритм технологии гидродинамической томографии. Синтезированные интервальные времена сопоставляются с реальными, а их разность составляет входные данные в итерационном алгоритме восстановления пространственного распределения фильтрационного сопротивления. Эта технология позволяет контролировать возникающие в процессе разработки месторождения зоны потери проницаемости пласта, ведущие к нарушению штатного режима работы месторождения. В результате локализации аномальных зон будут существенно снижены экономические затраты их ликвидации.

Библиографическая ссылка