Как известно, многие материалы, используемые на практике, при определенных условиях проявляют текучесть, для которой характерно отклонение от закона трения Ньютона [1]. Для решения задач о течении неньютоновских жидкостей успешно применяется метод математического моделирования, который предполагает построение адекватной математической модели течения и изучение её, например, с помощью реализуемых на компьютерах вычислительных алгоритмов. При этом требуется тщательное обоснование используемых алгоритмов. Такое обоснование тесно связано с изучением качественных свойств модели, в том числе c рассмотрением вопросов о существовании, единственности и регулярности решений соответствующей гидродинамической задачи.
В настоящей статье исследуется одна математическая модель, описывающая движение вязкоупругой жидкости типа Олдройда [11] в трёхмерной ограниченной области с непроницаемыми стенками. В уравнении состояния Олдройда используется полная производная. Важной особенностью рассматриваемой модели является то, что на границе области течения вместо классического условия прилипания задано условие проскальзывания Навье (обзор основных краевых условий, которые используются в механике жидкостей, приводится в [5]). Это условие определяет связь между скоростью скольжения жидкости и силой, действующей на жидкость со стороны межфазной границы «жидкость – твердое тело».
Следуя подходу Ж. Лерэ, мы вводим понятие обобщенного решения для соответствующей эволюционной задачи в классе подходящих функциональных пространств. Переход от классической постановки задачи к обобщенной постановке обусловлен тем, что при естественных ограничениях на данные модели, когда обобщенные решения могут быть сравнительно легко получены, классическое решение может и не существовать. В работе обсуждается алгоритм нахождения решений по методу Фаэдо– Галеркина.
Основной результат работы представлен в разделе 3, где сформулирована и доказана теорема о единственности, регулярности и энергетической оценке глобального, т.е. заданного на заранее выбранном промежутке времени [0, T], обобщенного решения. Эта теорема обобщает известные результаты Дж. Сэзера и Дж. Серрина [12] для трёхмерных эволюционных уравнений Навье–Стокса. Как и в случае системы Навье–Стокса, единственность решения начально-краевой задачи для модели Олдройда удается установить в классе, более узком, чем пространство, для которого известно существование решений. Тем не менее, полученные результаты демонстрируют связь между регулярностью и единственностью, а также дают возможность определить энергетические оценки решений.
Модель движения вязкоупругой жидкости в ограниченной области
Рассматривается математическая модель, описывающая движение несжимаемой вязкоупругой среды типа Олдройда в ограниченной трёхмерной области Ω с неподвижной непроницаемой границей Г класса С2 при краевом условии проскальзывания Навье:
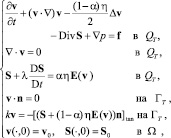(A)
где QT = Ω× (0, T) – пространственно-временной цилиндр c T > 0, ГT = Гт(0, T), v = v(x, t) – скорость, S = S(x, t) – упругая часть избыточных напряжений, p = p(x, t) – давление, E = E(v) – тензор скоростей деформации, E(v) = (∇v + (∇v)T)/2, f = f(x, t) – плотность внешних сил, D/Dt – полная (субстанциональная) производная,
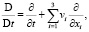
η, λ и α – положительные постоянные (η – вязкость, λ – время релаксации, α = 1 – λ-1κ – – параметр ретардации, где κ – время запаздывания, 0 < κ < λ), n = n(x) – единичный вектор внешней нормали к Г, k = k(x) – коэффициент проскальзывания, k(x) > 0, [·]tan – касательная составляющая вектора. Символы v0 и S0 обозначают соответственно поле скоростей и упругую часть избыточных напряжений при t = 0. Более подробное описание указанных физических величин приводится в [1].
Рассмотренную в этом разделе начально-краевую задачу для краткости будем называть задачей (A). Неизвестными в системе (A) являются вектор-функции v, S и функция p, а все остальные величины считаются заданными.
Обобщённая постановка задачи
Ниже мы будем использовать пространства Лебега и Соболева. Определения и свойства этих пространств систематически изложены в [8]. Скалярное произведение в L2(Ω) и L2(Г)) будем обозначать через (·, ·) и (·, ·)Г соответственно. Положим,
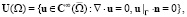
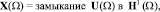
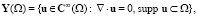
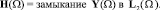
Предполагая, что функция k принадлежит пространству L∞(Г) и k(x) > k0 > 0, введем скалярное произведение в X(Ω) по следующей формуле:
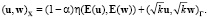
Из неравенства Корна следует, что норма, соответствующая этому скалярному произведению, эквивалентна норме, наследованной из пространства H1(Ω)
Следуя [6], будем отождествлять пространство H(Ω) c его сопряженным: H*(Ω) ≡ H(Ω). Поэтому имеем цепочку вложений: X(Ω)⊂H(Ω) ≡ H*(Ω)⊂X*(Ω).
Наконец, обозначим через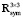 
пространство симметрических 3/3-матриц.
Теперь мы можем сформулировать определение обобщенного решения задачи (A). Пусть
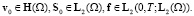
Определение. Обобщенным решением задачи (A) назовем пару вектор-функций
,
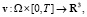
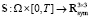такую, что
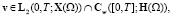
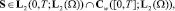
выполнены начальные условия: v(·,0) = v0 и S(·,0) = S0, а также следующие равенства
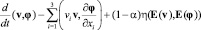
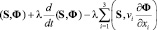
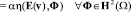
в смысле распределений на (0, T).
Замечание 1. Определение обобщенного решения задачи (А) в целом соответствует восходящей к работам Ж. Лерэ концепции слабых, или турбулентных, решений уравнений Навье–Стокса, которые с предельной тщательностью обсуждаются в фундаментальных трактатах О.А. Ладыженской [4] и Р. Темама [6].
Замечание 2. Как обычно, при рассмотрении обобщенных решений гидродинамических уравнений из определения решения «выпадает» давление p, которое после нахождения остальных неизвестных определяется с помощью результатов де Рама (см., например, [6, гл. I]).
Замечание 3. Для построения обобщенного решения может быть использован метод Фаэдо–Галеркина. Приведем основную идею данного метода. В подходящем функциональном пространстве выбирается базис. Затем вводится приближенное решение, которое записывается в виде суммы первых m базисных функций с коэффициентами, зависящими от t. Использование приближенных решений позволяет свести исходную начально-краевую задачу к задаче Коши для системы обыкновенных дифференциальных уравнений, решение которой не представляет существенных сложностей. Используя энергетические оценки и теоремы о компактности, можно выделить из последовательности приближенных решений подпоследовательность, которая сходится при m> к решению исходной задачи. На основе приведенной выше схемы в [7, 9] строятся решения различных типов начально-краевых задач для модели Олдройда; ряд стационарных задач о течении жидкости Олдройда рассмотрен в работах [2, 3, 10].
Основной результат работы
Введем обозначения:
M1 = L8(0, T; L4(Ω)),
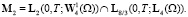
Теорема. Пусть пара вектор-функций (v, S) – обобщенное решение задачи (A), принадлежащее классу M = M1/M2. Тогда это решение (если оно существует) единственно в классе M, удовлетворяет включениям
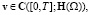
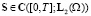
и энергетической оценке
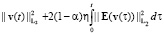
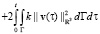
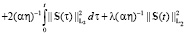
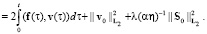
Доказательство. Пусть (v1, S1) и (v2, S2) – обобщенные решения из класса M. Покажем, что v1 = v2 и S1 = S2.
Проверим сначала, что
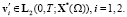(1)
Введем операторы:
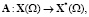
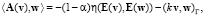
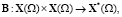
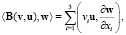
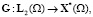
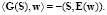
Из определения обобщенного решения следует, что
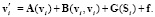
Очевидно, что имеют место включения:
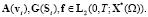(2)
Покажем, что
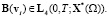(3)
Используя неравенство Гёльдера, находим, что
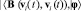
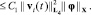
Здесь и ниже через Сi, i = 1, 2,…, обозначаются константы. Из полученной оценки и условий теоремы следует включение (3), которое вместе с (2) влечет (1).
Докажем теперь, что
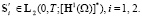(4)
Введем операторы:
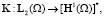
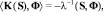
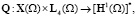
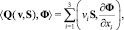
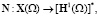
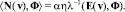
Из определения обобщенного решения следует, что
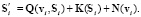
Очевидно, что
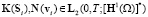. (5)
Используя неравенство Гёльдера, получаем, что
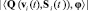
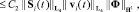
откуда, с учетом условий теоремы, вытекает, что
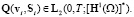
Это включение вместе с (5) влечет выполнение (4).
Принимая во внимание (1), (4) и применяя лемму 1.2 из [6, гл. III], получаем, что
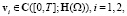
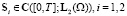
и п.в. на [0,T] выполнены равенства:
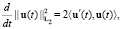(6)
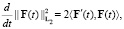(7)
где u = v1 – v2 и F = S1 – S2. Так как (v1, S1) и (v2, S2) – обобщенные решения задачи (A), то нетрудно вывести равенства:
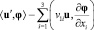
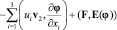
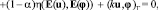
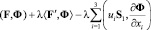
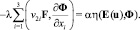
Полагая φ = u(t), Ф = (αη)-1F(t) и складывая полученные равенства, с учетом (6), (7) находим
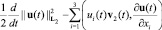
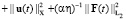
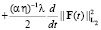
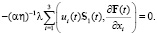(8)
Применяя неравенства Гёльдера, Юнга и теоремы о вложении пространств Соболева, находим, что
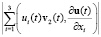
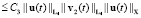
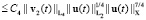
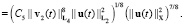
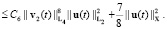(9)
Нам потребуется также следующая оценка:
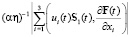
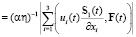
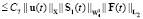
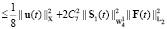. (10)
С учетом (9) и (10), мы выводим из равенства (8) следующую оценку:
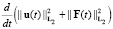
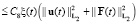
c функцией
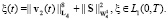
Поскольку u(0) = 0 и S(0) = 0, то, применяя лемму Гронуолла–Беллмана, получаем, что u = 0 и S = 0. Таким образом, мы установили, что в классе M не может быть более одного обобщенного решения задачи (A). Из приведенного выше доказательства видно, что если такое обобщенное решение существует, то оно принадлежит пространству C([0, T]; H(Ω))×C([0, T]; L2(Ω)). Энергетическая оценка обобщенного решения выводится аналогично оценке (8) с последующим интегрированием в пределах от 0 до t.
Работа выполнена при финансовой поддержке РФФИ, грант № 16-31-00182 мол_а.
Библиографическая ссылка
Барановский Е.С., Артемов М.А. ОБ ОДНОЙ МОДЕЛИ ДВИЖЕНИЯ ВЯЗКОУПРУГОЙ ЖИДКОСТИ С ПРИСТЕННЫМ СКОЛЬЖЕНИЕМ // Современные наукоемкие технологии. – 2016. – № 8-1. – С. 27-31;URL: https://top-technologies.ru/ru/article/view?id=36096 (дата обращения: 21.11.2024).