Рациональная структура ремонтно-обслуживающей базы эксплуатирующих технику предприятий, а также предприятий технического сервиса и ремонта определяется, в первую очередь, перечнем и производственной мощностью специализированных участков по ремонту и замене деталей и сборочных единиц, отличающихся друг от друга по назначению и устройству различных систем, из которых состоит любая лесная, в первую очередь, лесозаготовительная машина [1, 9]. Рациональная организация работы предприятий технического сервиса и ремонта любой техники определяет их собственную эффективность, а также эффективность технической и общей технологической эксплуатации обслуживаемой и ремонтируемой техники [2, 10].
Особенно эти вопросы важны и наукоемки для сервисных и ремонтных предприятий как объектов массового обслуживания открытого типа, для которых важны результаты исследования интенсивности потока отказов обслуживаемой техники, определяющие поток заявок, его интенсивность, распределение времени между заявками и, если поток заявок простейший, то его стационарность, ординарность, отсутствие последействия [6, 11].
Последовательность следующих во времени друг за другом отказов деталей и сборочных единиц образуют поток отказов, как поток случайных событий. Для решения задач технической эксплуатации и технического сервиса машин и оборудования необходимы характеристики потока отказов каждого из элементов машин в парке восстанавливаемой и ремонтируемой техники одной марки.
Вид потока отказов, изучение суперпозиции потоков отказов одноименных деталей нескольких машин, вычисление характеристик потока отказов конкретных деталей парка восстанавливаемых машин одной марки с оценкой интенсивности отказов, распределения промежутка времени между отказами являются исходной информацией для проектирования и расчета специализированных участков предприятий по техническому обслуживанию и ремонту техники [2, 4, 9].
В теории вероятностей различают следующие основные случайные потоки событий: пуассоновский, винеровский, Пальма. Случайные потоки характеризуются свойствами, важнейшими из которых являются: последействие, ординарность, стационарность. Если поток событий – отказов, не имеет последействия, ординарен и стационарен, он называется простейшим или стационарным пуассоновским процессом [3, 9].
Подтверждение гипотезы о простейшем потоке упрощает решение задач технической эксплуатации и технического сервиса, позволяет определять интенсивность технических воздействий.
При определении показателей безотказности и долговечности объектов используют различные планы испытаний [9]. Согласно плану [NUN] контролируется N объектов, испытания заканчиваются после достижения предельного состояния всеми объектами без их восстановления или замены. По результатам испытаний оцениваются закон распределения до первого отказа и статистические характеристики безотказности и долговечности деталей.
В случае реальной рядовой эксплуатации объект после его отказа восстанавливают или заменяют новым. После истечения первых n интервалов эксплуатации восстанавливаемого парка машин, процесс возникновения отказов стабилизируется в соответствии с законом распределения Пуассона. Вероятность появления k отказов объекта за наработку от нуля до t, то есть F(k, t), равна [8, 9].
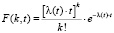 , (1)
, (1)
где λ(t) – интенсивность отказов.
Интенсивность отказов λ(t) связана с вероятностью отказа F(t) на интервале (t, t + dt) зависимостью [9]:
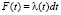 . (2)
. (2)
Можно считать, что интенсивность отказов в законе Пуассона есть не что иное, как вероятность отказа в единицу наработки. Проверка гипотезы о стационарности идентична проверке гипотезы о равномерном законе распределения. После стабилизации процесса возникновения потока отказов в пределах каждого интервала n интенсивность отказов является постоянной и равной λ.
Вероятность появления k отказов объекта Fn(k) на интервале n равна [9]:
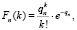 (3)
(3)
где qn – вероятность возникновения отказа объекта на n-м интервале с учетом наличия отказов на предыдущих интервалах. Методика вычисления значения qn изложена в работе [9]. В частном случае при k = 1 имеем:
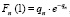 . (4)
. (4)
Необходимым условием применимости распределения Пуассона и, следовательно, формулы (7) является достаточно малое значение вероятности отказа qn. При 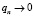
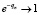 . Полагая, что длительность процесса восстановления мала по сравнению с длительностью работы объекта, отказы независимы друг от друга, интенсивность отказов постоянна, т.е. поток отказов носит стационарный характер.
. Полагая, что длительность процесса восстановления мала по сравнению с длительностью работы объекта, отказы независимы друг от друга, интенсивность отказов постоянна, т.е. поток отказов носит стационарный характер.
Для экспериментального исследования и подтверждения гипотез о соответствии простейшему потоку характера потока отказов деталей лесных машин необходимо определить характеристики законов распределения ресурсов деталей с проведением статистической обработки экспериментальных данных потоков отказов деталей машин.
Алгоритм методики проверки соответствия потока отказов деталей машин простейшему потоку
А. Проверка на отсутствие последействия
Аналитическое условие принадлежности к классу потоков без последействия записывается согласно работе [3, 9] в следующем виде:
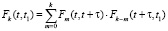
при
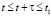 , (5)
, (5)
где 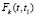 – вероятность возникновения k отказов в течение времени t1 – t.
– вероятность возникновения k отказов в течение времени t1 – t.
Отсутствие последействия определяется условием, при котором отказы являются событиями случайными, независимыми, и если объект проработал до момента τ и промежуток времени на отказ распределен по показательному закону, то вероятностные характеристики безотказной работы объекта сохраняются в дальнейшем, независимо от времени протекания этого промежутка.
Для проверки гипотезы осуществляется построение эмпирических законов распределения и определение числовых параметров. В качестве критерия используется критерий согласия Пирсона или Колмогорова.
Б. Проверка на ординарность
Условие принадлежности к классу ординарных потоков записывается в виде [3, 9]:
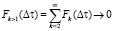 при
при 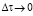 . (6)
. (6)
Условие ординарности означает, что вероятность появления в малом интервале Δτ двух и большего числа событий есть величина высшего порядка малости по сравнению с вероятностью появления в этом интервале одного события.
Для проверки гипотезы об ординарности потока отказов элементов машин определяется частота отказов за некоторый малый промежуток времени нескольких (двух и более) элементов. Продолжительность контрольного отрезка может быть принята равной одной рабочей смене.
В. Проверка на стационарность
Поток отказов принадлежит классу стационарных потоков, если вероятность возникновения фиксированного числа отказов на заданном интервале времени зависит только от длины интервала, а не от того, где на оси времени расположен этот интервал. Условие стационарности потока имеет вид [3, 9]:
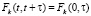 . (7)
. (7)
Стационарность потока событий подтверждается малой изменчивостью интенсивности отказов, отсутствием тренда, т.е. отсутствием изменения интенсивности потока отказов. Теоретически это объясняется стабилизацией интенсивности и частоты отказов с течением времени, т.е. стремлением к некоторой постоянной величине.
В теории массового обслуживания доказывается, что каждый ординарный поток без последействия и с ограниченным последействием через некоторое время становится близким к стационарному [3, 4, 5].
Проверка гипотезы стационарности потока отказов элементов машин может быть осуществлена при двух возможных условиях:
a) когда отклонение параметра потока отказов не имеет ярко выраженного уменьшения (или увеличения) с течением времени;
б) когда параметр потока отказов имеет тенденцию к уменьшению (или увеличению) с течением времени.
В первом случае, если статистических данных достаточно и в каждом интервале Δt имеется не менее 5–8 наблюдений, то проверка гипотезы о стационарности идентична проверке гипотезы о равномерном законе распределения с использованием обычных критериев, применяющихся для проверки гипотезы о сходимости теоретического и статистического распределений. Например, можно использовать критерий χ2:
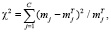 (8)
(8)
где mj – число отказов в i-м интервале;
mjT – теоретическое количество отказов в j-м интервале;
C – количество интервалов, на которые разбивается размах наработки на отказ.
Если статистическое значение критерия, найденное по формуле, меньше табличного (критического) значения, то гипотеза о стационарности потока не отвергается, и наоборот. 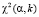 определяется при уровне значимости «a» и числе степеней свободы k = c – 2, так как рассматривается закон равномерной плотности однопараметрический.
определяется при уровне значимости «a» и числе степеней свободы k = c – 2, так как рассматривается закон равномерной плотности однопараметрический.
При проверке убывающего характера параметра потока (как и вообще при любой проверке статистической гипотезы) выдвигаются две гипотезы: нулевая – об отсутствии тенденции к уменьшению параметра потока и альтернативная – о наличии тенденции.
Апробация методики и результаты проверки на стационарность
Проверим гипотезу стационарности потока отказов по данным наблюдений за девятью лесными машинами на примере штока гидроцилиндра привода сучкорезной головки. Исходные данные, полученные авторами о наработке между отказами, возникшими в условиях рядовой эксплуатации, приведены в табл. 1. Методика изложена в работе [9].
Обозначим через Lj – число отказов, когда более ранняя наработка j – го объекта является меньшей из более поздних. Это число является величиной случайной, оценка математического ожидания M[Lj], дисперсии D[Lj] и среднеквадратического отклонения σ[Lj] которой определены по известным формулам нормальной функции распределения [7] и приведены в табл. 2.
Величину Lj следует центрировать и нормировать, то есть ввести в рассмотрение величину Zj, которая вычисляется по формуле [7]:
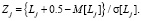 (9)
(9)
Таблица 1
Наработка между отказами штока гидроцилиндра лесной машины
|
Номер отказа |
Номер машины |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Наработка машины, моточас. |
|||||||||
|
1 |
1439 |
212 |
331 |
226 |
863 |
1500 |
248 |
250 |
700 |
|
2 |
1110 |
1632 |
1036 |
352 |
334 |
||||
|
3 |
1362 |
713 |
234 |
1312 |
314 |
||||
|
4 |
403 |
286 |
|||||||
|
5 |
283 |
||||||||
|
6 |
324 |
||||||||
Таблица 2
Оценка математического ожидания, дисперсии и среднеквадратического отклонения величины Lj
|
Номер машины |
mj |
Lj |
M[Lj] |
D[Lj] |
σ[Lj] |
Zj |
|
1 |
1 |
0 |
0,25 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0,25 |
0 |
0 |
0 |
|
3 |
4 |
4 |
3,0 |
2,17 |
1,47 |
1,019 |
|
4 |
3 |
2 |
1,5 |
0,92 |
0,96 |
1,044 |
|
5 |
1 |
0 |
0,25 |
0 |
0 |
0 |
|
6 |
1 |
0 |
0,25 |
0 |
0 |
0 |
|
7 |
3 |
1 |
1,5 |
0,92 |
0,96 |
0 |
|
8 |
3 |
3 |
1,5 |
0,92 |
0,96 |
9,088 |
|
9 |
6 |
3 |
7,5 |
7,08 |
2,66 |
– 1,503 |
|
Итого |
23 |
2,648 |
Для вычисления статистического значения критерия по совокупности наблюдений за N объектами используется выражение [9]:
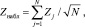 (10)
(10)
где N – количество объектов, за которыми велось наблюдение. Эта величина может меняться в зависимости от длительности наблюдений за каждым объектом.
Тогда условие проверки гипотезы примет вид
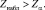 (11)
(11)
По данным табл. 1 подсчитаем число случаев Lj, когда более ранняя наработка меньше одной из блока поздних, затем определим и сравним значения Zнабл и Z0,1, согласно данным табл. 2.
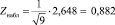 ;
;
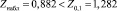 .
.
При уровне значимости a = 0,1 квантиль нормального распределения Z0,1 = 1,282 [7], а условие стационарности Zнабл < Z0,1 = 1,282.
Гипотеза о стационарности потока отказов рассматриваемой детали – штока гидроцилиндров лесной машины – не отвергается, поскольку выполняется условие Zнабл < Zα (при α = 0,1). Экспериментальными исследованиями авторов [9] установлено, что сходимость к простейшему потоку суммарного потока отказов элементов технологического оборудования отечественных лесозаготовительных машин при Вейбулловском и нормальном законе распределения ресурса деталей зависит от величины ресурса, коэффициента его вариации, числа суммируемых потоков и наблюдается при суммировании 5–7 и более потоков.
Выводы
1. В работе представлена и апробирована методика исследования потока отказов деталей лесных машин с целью проверки их на соответствие простейшему потоку.
2. Выявленные характеристики простейшего потока отказов деталей и элементов восстанавливаемого парка машин позволяют определить интенсивность и объем заявок на ремонтные работы и спланировать их выполнение на специализированных участках предприятий технического сервиса, в том числе на станциях обслуживания и ремонта машин, как на объектах массового обслуживания открытого типа.
3. Результаты проведенных исследований показали положительную сходимость к простейшему потоку суммарных потоков одноименных элементов технологического оборудования отечественных лесозаготовительных машин при суммировании 5–7 и более единичных потоков.
4. Методика исследований может быть распространена на определение характеристик потоков отказов элементов конструкций других, в том числе зарубежных, машин.
Библиографическая ссылка
Шиловский В.Н., Питухин А.В., Костюкевич В.М. ИССЛЕДОВАНИЕ ПОТОКА ОТКАЗОВ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ЛЕСНЫХ МАШИН // Современные наукоемкие технологии. 2016. № 7-1. С. 94-98;URL: https://top-technologies.ru/ru/article/view?id=36067 (дата обращения: 05.03.2026).



