Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шабанова В.Г. 1 Мамедова Т.Ф. 1 Каледин О.Е. 1 Шабанов Г.И. 1

---

1 ФГБОУ ВПО «Мордовский государственный университет им. Н.П. Огарёва» (национальный исследовательский университет)

Настоящая статья посвящена исследованию экономико-математических моделей, позволяющих найти варианты оптимального развития экономики отрасли. Представлено теоретическое исследование управления произвольным объектом. Рассмотрена задача оптимального управления на примере многоотраслевой экономики. В качестве практического примера применения достаточных условий оптимальности рассмотрена однопродуктовая экономическая система. Данная модель позволяет изучить свойства и тенденции изменения взаимосвязанных агрегированных показателей. В качестве управления в данной задаче выбрана функция, характеризующая долю непроизводственного потребления. Для решения задачи необходимо определить максимальное среднедушевое потребление на исследуемом интервале времени, представленное критерием качества. Уравнение движения в относительных переменных принимает вид дифференциального уравнения роста капиталовооружённости. Введены ограничения на управление: производительность труда и основные производственные фонды отрасли. Построенная задача – линейная по управлению. В качестве состояния системы выступает капиталовооружённость а управления – доля потребления. Первый показатель входит в уравнение движения под знаком производной и самостоятельно, второй – только самостоятельно.

Статья в формате PDF

0 KB

математическая модель

межотраслевой баланс

оптимальное управление

дифференциальные уравнения

отраслевые экономические показатели

критерии качества управления

динамические объекты

1. Лагоша Б.А. Оптимальное управление в экономике: Учебное пособие. / Московский государственный университет экономики, статистики и информатики – М., 2004. – С. 35–36.

2. Мамедова Т.Ф. Математическая модель стабилизации производства. – Математическое моделирование и краевые задачи. Труды тринадцатой межвузовской конференции. – 2003. – С. 67–69.

3. Мамедова Т.Ф. Математическое моделирование экономических процессов: учебное пособие. – Саранск: Изд-во СВМО, 2009. – С. 34–37.

4. Шабанова В.Г., Мамедова Т.Ф., Шабанов Г.И. Модель управления финансово-экономической деятельностью производственного предприятия агропромышленного комплекса. – Научный журнал «Фундаментальные исследования». – 2016. – № 3–1. – С. 67–71.

5. Шабанова В.Г. Анализ методов представления знаний в модели управления экономическими показателями предприятия. – Научный альманах: международный сборник научных трудов – Тамбов: Изд-во UCOM, 2015. – С. 539–542.

Современные автоматизированные системы оперативного мониторинга текущего состояния управления экономикой группы отраслевых предприятий помогают руководителям повысить эффективность принятия стратегических финансово-хозяйственных решений. Однако имеющееся математическое обеспечение таких систем требует дальнейших исследований экономико-математических моделей (ЭММ) позволяющих найти варианты оптимального развития экономики отрасли [5].

Межотраслевой баланс производства и распределения общественного продукта представляет собой систему показателей, отражающих производство и распределение общественного продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода [2]. По периоду анализа модели межотраслевого баланса подразделяются на два типа. Если процесс производства в межотраслевом балансе рассматривается в течение нескольких лет, причем результаты первого года определяют условия производства во втором году, то система является динамической. Особенностью динамических межотраслевых балансов является то, что в них из состава конечного использования исключаются капиталовложения, являющиеся функцией выпусков отраслей в последующие годы. Динамические межотраслевые балансы значительно точнее описывают развитие экономики, чем любые другие экономико-математические методы [3].

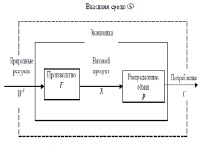
Рис. 1. Взаимосвязь элементов производства

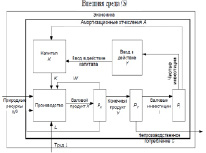
Рис. 2. Взаимодействие факторов производства

Другим типом межотраслевого баланса являются статические балансы, в которых капиталовложения включены в состав конечного использования. Таким образом, статические межотраслевые балансы составляются для одного года, а динамические – за несколько лет.

Основной составляющей производственно-технологической модели экономики является взаимосвязь элементов производства вне общественной формы реализации продукции (рис. 1). Синергетическое взаимодействие трудовых факторов L, средств труда (основные производственные фонды, капитал K) и предметов труда (WS) является производственными ресурсами (рис. 2). И как следствие, результатом производственной деятельности является валовой продукт (X), распределяемый в блоке PХ на производственное потребление (W) и конечный продукт (Y). В свою очередь, конечный продукт (Y) делится в блоке распределения PY на валовые капитальные вложения (I) и на непроизводственное потребление (C) [1].

Математическое моделирование компонентов системы экономики отрасли часто приводит к необходимости решения распределительных задач смешанного дискретно-непрерывного типа с нелинейными производственными функциями. Данный тип задач занимает значительное место среди приложений математического программирования [4].

При изучении нелинейных ЭММ целесообразно использовать методы оптимального управления. Решение задач данными методами характеризуется наличием некоторого динамического объекта, т.е. объекта, состояние которого изменяется во времени. Для примера проведём исследование управления произвольным объектом. Предположим, что по условию его положение в каждый момент времени t полностью характеризуется набором параметров x1(t), … xn(t). Вектор x(t) = (x1(t), … xn(t)) является фазовым вектором объекта, движением которого можно управлять. В этом случае, в каждый момент времени t, управление будет характеризоваться определённым набором параметров u1(t),...um(t). При этом вектор u(t) = u1(t),...um(t) является управляющим параметром объекта или просто управлением. Необходимо отметить, что состояние объекта в данный момент времени t зависит от того, какие значения принимает управление u(t) и не зависит от будущего поведения управления.

Зависимость вектора фазового состояния x(t) от управления u(t) может описываться системой дифференциальных уравнений 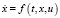. В этом случае, зная значения управления u(t) в каждый момент времени t, можно определить траекторию объекта x(t), как решение дифференциального уравнения .

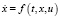Предположим, что задан начальный момент времени t0 и множество M0 допустимых начальных состояний объекта. Желательно управлять объектом так, чтобы в конечный момент времени t1 объект перешел на некоторое множество M1 допустимых конечных состояний.

Может случиться, что управляемый объект можно перевести из множества M0 на M1 несколькими способами. На практике желательно среди всех таких способов выбрать наилучший в определенном смысле. Для этого каждому допустимому управлению u(t), заданному на отрезке [t0, t1], и соответствующей ему траектории объекта x(t) сопоставлено некоторое число J, оценивающее качество пары u(t), x(t), то есть, задан функционал или критерий качества.

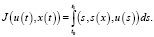
Таким образом, задача оптимального управления заключается в нахождении такого допустимого управления u*(t) и соответствующей ему траектории x*(t), переводящей объект из множества начальных состояний M0 на множество конечных состояний M1, что при этом функционал качества J(u(t), x(t)) принимает минимальное значение, то есть:

.

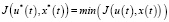Введение нелинейных производственных функций в межотраслевой баланс позволяет учесть возможность взаимного замещения труда и фондов в отраслях и зависимость производительности труда от фондовооруженности [3].

Теперь рассмотрим задачу оптимального управления на примере многоотраслевой экономики. В качестве практического примера применения достаточных условий оптимальности рассмотрим однопродуктовую экономическую систему, характеризующуюся в каждый момент времени t (время непрерывное) следующими переменными:

X – интенсивность выпуска валового продукта отрасли в рассматриваемый период;

Y – интенсивность конечного продукта отрасли, идущего на непроизводственное потребление (продажу);

C – величина непроизводственного потребления (спрос);

K – капитал (объем основных производственных фондов отрасли – ОПФ);

L – трудовые ресурсы отрасли (живая сила);

I – инвестиции (валовые капитальные вложения отрасли).

С помощью этой модели изучают свойства и тенденции изменения взаимосвязан-ных агрегированных показателей, таких как валовой и конечный продукты, трудовые ресурсы, производственные фонды (капитал), инвестиции, потребление и т.д. Каждая отрасль в данной межотраслевой экономической модели идентифицируется отраслевым уровнем воспроизводства основных фондов:

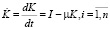
или

(1)

где µ – коэффициент амортизации.

Данное соотношение показывает, что валовые инвестиции расходуются на прирост капитала и восстановление ОФП за счет амортизационных отчислений.

Открытая система межотраслевых связей представлена балансовым соотношением:

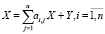. (2)

В свою очередь, конечный продукт разделятся на валовые инвестиции и непроизводственное потребление:

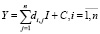. (3)

Здесь матрица коэффициентов ai,j (технология производства) – матрица коэффициентов прямых затрат, которая показывает, какое количество продукции i-й отрасли расходуется на производство одной единицы продукции отрасли j. Экономический смысл матрицы коэффициентов di,j следующий: они показывают, какое количество продукции i-й отрасли должно быть вложено в j-ю отрасль для увеличения выпуска ее продукции на единицу в рассматриваемых единицах измерения. Коэффициенты di,j называются коэффициентами капитальных вложений или коэффициентами приростной фондоемкости.

В качестве управления в данной задаче целесообразно выбрать функцию , характеризующую долю непроизводственного потребления.

Тогда для одной отрасли экономики уравнение (1) с учетом (2) и (3) примет вид

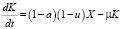, (4)

где 0 ≤u ≤ 1, поскольку доля непроизводственного потребления может приближаться к нулю в случае, когда непроизводственное потребление минимально и весь конечный продукт используется для дальнейшего производства, и приближаться к единице, в случае, когда весь конечный продукт используется только для получения дохода от реализации.

Так как размеры валового продукта определяются заданной функцией, которая ограничивает производственный потенциал отраслей и характеризует возможности производства в зависимости от величины объема основных производственных фондов отрасли K, трудовых ресурсов L, изменяющихся во времени t:

0 ≤ X ≤ F(t, K, L), (5)

В данной задаче будем рассматривать непрерывную и дважды дифференцируемую производственную функцию F(t, K, L) с учетом автономного научно-технического прогресса. При рассмотрении производства на макроуровне, будем учитывать, что факторы производства меняются непрерывно, а выпуск продукции изменяется достаточно гладко при изменении факторов.

Решение будем искать при условии K ≥ P, где P – заданный уровень ОПФ. Пусть заданы основные производственные фонды в начальный и конечный момент времени:

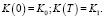(6)

Тогда искомый процесс представлен совокупностью функций ν = (K(t), X(t), u(t)), удовлетворяющих уравнению (4) и условиям (5) – (6). Здесь X – состояние экономической системы в момент времени t, u – выбранное управление. Очевидно, что такой процесс не единственный.

Далее осуществим поиск процесса v, который характеризует оптимальный путь развития экономики на отрезке времени [0, T] и максимизирует дисконтированное суммарное среднедушевое потребление. Уравнение движения имеет вид

.

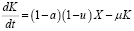С начальными данными K(0) = K0; K(T) = K1 и ограничениями 0 ≤ u ≤ 1, 0 < a < 1. Необходимо определить максимальное среднедушевое потребление на исследуемом интервале времени [0, T] с учетом дисконтированного (приведенного к начальному моменту) потребления:

, (7)

где δ – коэффициент дисконтирования.

Задача нахождения оптимального пути развития экономики на интервале времени [0, T] формулируется следующим образом: при заданном уравнении движения

,

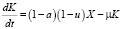ограничении на управление 0 ≤ u ≤ 1, фазовых ограничениях 0 ≤ a ≤ , краевых условиях K(0) = K0; K(T) = K1 и критерии оптимальности

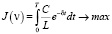
определить управление, при котором заданный критерий принимает максимальное значение.

Далее необходимо сопоставить однородные показатели экономической системы. Это позволит сделать замена переменных, которая приводит их к удельным показателям на душу населения. Далее определяем следующие относительные переменные:

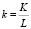– капиталовооруженность;

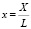– производительность труда;

– среднедушевое потребление.

Согласно правилу дифференцирования получаем:

.

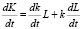Тогда уравнение движения (4) примет следующий вид:

Будем считать выбранный отрезок времени непродолжительным, тогда прирост трудовых ресурсов осуществляется с постоянным темпом:

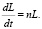
Отсюда получим

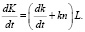
Тогда уравнение движения в относительных переменных примет окончательный вид:

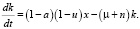(8)

Уравнение (8) назовем дифференциальным уравнением роста капиталовооруженности. При этом ограничение на управление остается следующим:

0 ≤ u ≤ 1, (9)

а ограничение на производительность труда x примет следующий вид:

0 ≤ x = f(t, k), (10)

где 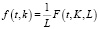– функция производительности одного работника.

Ограничения на основные производственные фонды отрасли можно заменить ограничениями на капиталовооруженность:

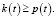(11)

Из краевых условий (6) получим начальное и конечное значения капиталовооруженности:

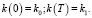(12)

В результате преобразования функционала (7) к относительным переменным получим выражение вида

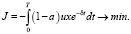(13)

Итак, задача сводится к определению процесса ν = (k(t), x(t), u(t)), который обращает в минимум функционал (13) при условиях (9)–(12).

Таким образом, построенная задача – линейная по управлению u c ограничением на управление (9). Здесь в качестве состояния системы выступает капиталовооруженность k, а управлением – доля потребления u. Причем первый показатель входит в уравнение движения (8) под знаком производной и самостоятельно, а второй – только самостоятельно.

Библиографическая ссылка