Для организации сетей VPN существует множество решений, которые можно разбить на две части: первое – организация транспортировки данных, вторая – организация защиты передаваемых данных. Для организации защиты передаваемых данных существует множество алгоритмов для шифрования и аутентификации, для согласования параметров которых существуют решения в виде набора протоколов IPsec или PPP. Для организации транспортировки данных между филиалами предприятия без гарантий качества обслуживания достаточно воспользоваться любым туннельным протоколом и иметь доступ к сети Internet. В случае же если необходима гарантия доставки данных с заданным качеством обслуживания, то на сегодняшний день такое решение у провайдеров в основном связано с технологией MPLS [1, 5, 8, 12]. Технология MPLS совместно с такими протоколами динамической маршрутизации OSPF или IS-IS, а также с протоколом резервирования ресурсов RSVP (Resource Reservation Protocol), позволяет динамически организовывать виртуальные каналы с заданной пропускной способностью. Это достигается за счет того, что протоколы маршрутизации в каждом маршрутизаторе формируют топологическую базу данных о сети, в которой находится информация о скорости каналов связи и доступной полосе пропускания, а также ряд дополнительных атрибутов. Располагая такой информацией, с помощью алгоритма CSPF [9, 13] (constrained shortest path first – алгоритм выбора наикратчайшего маршрута с ограничениями) вычисляется маршрут, который удовлетворяет требованиям необходимой полосы пропускания, затем по вычисленному маршруту отправляются сообщения протокола RSVP, которые резервируют необходимую полосу пропускания и формируют таблицу пересылки по меткам, после чего топологическая информация в базах данных обновляется. Данный алгоритм формирования виртуальных маршрутов не является полностью динамическим, так как требует создания так называемых туннельных интерфейсов [5], туннельные интерфейсы создаются на граничных маршрутизаторах, параметрами такого интерфейса является адрес узла назначения и необходимая полоса пропускания, которую необходимо зарезервировать между парой граничных маршрутизаторов, к которым подключены сайты одной VPN сети. Количество туннелей между каждой парой граничных маршрутизаторов и необходимая скорость для резервирования каждым туннелем является неопределенной величиной. Целью данной статьи является разработка метода получения математической модели, позволяющей проводить анализ загруженности каналов связи, в результате которой можно определить необходимое число туннелей и необходимую резервируемую полосу пропускания для каждого туннеля.
Текущие методы анализа сетей, в том числе VPN, базируются либо на граф комбинаторных алгоритмах [11], либо на математическом аппарате теории массового обслуживания [4]. В данной статье предложен метод на основе тензорного анализа, согласно которому сеть можно рассматривать как совокупность геометрических объектов в пространстве, размерность которого определяется топологией сети. Преимуществом данного подхода является простота алгоритма формирования математической модели, описывающей состояние сети в виде системы линейных уравнений, решение которого в зависимости от накладываемых ограничений обеспечивает распределение трафика между сайтами VPN сети с заданными параметрами качества обслуживания.
Постановка задачи
Исходными данными для анализа VPN сети служит топология сети провайдера, предоставляющего услуги VPN, матрица запросов между отдельными сайтами VPN, потоки между сайтами VPN, как правило, задаются в виде матрицы запросов, представляющей собой матрицу размерности DxD, где элемент dij показывает интенсивность потока от i-го сайта до j-го сайта одной сети VPN.
Анализируемыми характеристиками являются интенсивность поступления трафика и загрузка каналов связи при ограничениях на параметры качества обслуживания. В результате анализа будут определены маршруты прохождения трафика между каждой парой сайтов. Пусть топология сети провайдера представлена в виде ориентированного графа G(N,A), где каждое ребро графа определяет однонаправленный канал связи. Как известно из [2, 7], в качестве математической модели однонаправленного двухточечного канала связи может выступать одноканальная система массового обслуживания, так как алгоритм обслуживания пакетов в интерфейсе маршрутизатора/коммутатора соответствует модели обслуживания одноканальной СМО. Таким образом, в качестве модели всей сети выступает сеть массового обслуживания. Граф сети массового обслуживания может быть описан матрицей инцидентности I, каждый элемент которой равен – 1 или 1 и показывает направление ветви.
Общий подход к решению задачи тензорным методом
Основной идеей тензорного метода является то, что все топологии, содержащие одинаковое число ветвей, связаны между собой тензором преобразования, в роли которого могут выступать матрица линейно независимых разрезов или матрица линейно независимых контуров, или объединенная матрица линейно-независимых контуров и разрезов.
Поскольку все сети с топологией, состоящей из одинакового числа ветвей, связаны между собой тензором преобразования, то среди множества проекций можно выделить так называемую примитивную сеть [6]. Примитивная сеть состоит из такого же количества ветвей, как и исследуемая сеть, но количество несвязанных компонент в ней также равно числу ветвей, в связи с чем, потоки в каждой ветви примитивной сети оказываются независимыми. Топология примитивной контурной сети показана на рис. 1. Как видно в примитивной контурной сети, каждой контурной интенсивности соответствует интенсивность в соответствующей ветви.
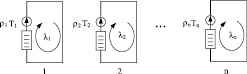
Рис. 1. Примитивная контурная сеть
Топология примитивной узловой сети показана на рис. 2. Как видно в примитивной узловой сети, каждой узловой интенсивности соответствует интенсивность в соответствующей ветви. Под узловой интенсивностью можно понимать сумму потоков, втекающих или вытекающих из узлов.
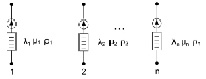
Рис. 2. Примитивная узловая сеть
Если определить математическую модель простейшего элемента сети, которым является одноканальная СМО, как ρ = tλ или λ = µρ [4], то, согласно постулату обобщения Крона, если известна математическая модель, описывающая поведение простейшего элемента, то и система, состоящая из совокупности простейших элементов, будет описана такой же математической моделью только в матричном виде. Следовательно, математическая модель примитивной сети имеет тривиальный вид, и для примитивной контурной сети показывает связь контурных интенсивностей с контурными временами обслуживания и контурными загрузками.
, (1)
где
λi (i = 1…n) – интенсивность поступления, поступающая на вход элемента сети;
ti (i = 1…n) – среднее время обслуживания;
ρi (i = 1…n) – загрузка i-го элемента.
Или в тензорном виде:
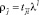. (2)
Математическая модель примитивной узловой сети имеет тривиальный вид и показывает связь узловых интенсивностей с узловыми интенсивностями обслуживания и узловыми загрузками.
, (3)
где
λi (i = 1…n) – интенсивность поступления, поступающая на вход, элемента сети;
µi (i = 1…n) – интенсивность обслуживания;
ρi (i = 1…n) – загрузка i-го элемента.
Или в тензорном виде:
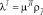. (4)
В данной статье рассматриваются так называемый ортогональные сети, то есть сети, которые содержат как замкнутые пути, так и разомкнутые, такие сети можно анализировать, приводя их к одному из двух типов сетей, либо к контурной, либо к узловой [6]. При анализе таких сетей в начале необходимо было определить тензор преобразования от примитивной сети к анализируемой, и после ряда преобразований получалась финальная система линейных уравнений.
Наряду с существующими двумя подходами можно предложить метод анализа ортогональных сетей [6], в котором не требуются преобразования над исходной сетью. В таком случае примитивная сеть для ортогональной сети будет состоять из набора примитивных узловых элементов и набора контурных элементов.
Таким образом, в ортогональной сети базисными элементами будет совокупность линейно независимых контуров и линейно независимых разрезов. Следовательно, необходимо установить следующее преобразование:
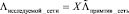, (5)
где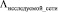 
– вектор, содержащий как узловые, так и контурные интенсивности в исследуемой сети;
– вектор примитивных элементов, содержащий как контурные, так и узловые примитивные элементы;
Х – тензор преобразования.
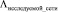для краткости будем называть вектором фазовых [3] интенсивностей исследуемой сети, а 
фазовых интенсивностей примитивной сети.
Определим структуру тензора преобразования X.
Выражения (5) можно записать развернутом виде:
(6)
Как видно из (6), тензор преобразования X состоит из двух составляющих, тензора А, который связывает узловые интенсивности примитивной сети с узловыми интенсивностями исследуемой сети, и тензора преобразования C', который связывает контурные интенсивности примитивной сети с контурными интенсивностями исследуемой.
Правило получения тензора А аналогично, тому как это было в [6], когда правило получения матрицы C', заключается в том, что необходимо однозначно сопоставить одной контурной интенсивности примитивной сети только одну контурную интенсивность исследуемой сети. А как известно из теории графов, совокупность всех ребер графа делится на ветви и хорды, то есть контурная интенсивность в исследуемой сети соответствует интенсивности в той ветви примитивной сети, которая после преобразования в исследуемую сеть стала хордовым ребром.
Ниже приведем пример получения матрицы Х. Пусть рассматривается сеть массового обслуживания, структура которой представлена на рис. 3. Для данной СеМО введены линейно-независимые контурные интенсивности λα, λβ, λγ, и линейно-независимые узловые интенсивности λi i∈(1..9).
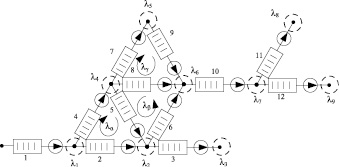
Рис. 3. Анализируемая СеМО
Система уравнений (6) для исследуемой СеМО будет выглядеть следующим образом:
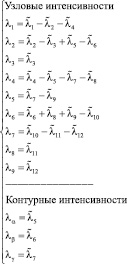(7)
В матричном виде система уравнений (7) будет выглядеть следующим образом:
Для получения тензора преобразования между примитивной и анализируемой сетью можно воспользоваться математическим аппаратом теории графов, согласно которому переход между узловыми интенсивностями примитивной к узловым интенсивностям анализируемой сети обеспечивается с помощью матрицы инцидентности без одной строки, а связь между контурными интенсивностями обеспечивается с помощью матрицы хорд. Соответственно, если придерживаться обозначений теории графов, то систему уравнений можно записать в виде
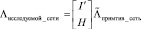, (8)
где I’ – матрица инцидентности без линейно-независимой строки;
Н – матрица хорд графа.
Алгоритмы получения этих матриц известны, и сложность этих алгоритмов растет линейно с ростом числа ветвей в сети. Обозначим тензор преобразования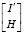 
за X, тогда уравнение (8) можно привести к следующему виду:
.
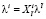Соответственно, проводя анализ по Крону [6], можно убедиться в справедливости следующих соотношений:
,
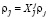где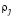 
– фазовые загрузки примитивной сети;
ρj – значение фазовых загрузок исследуемой сети.
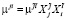, (9)
µji – матрица фазовых интенсивностей обслуживания исследуемой сети;
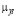– матрица фазовых интенсивностей обслуживания примитивной сети.
На основании полученных значений фазовых интенсивностей поступления и фазовых интенсивностей обслуживания значения фазовых загрузок исследуемой сети будут определяться как
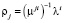. (10)
А значение загрузок в каждой ветви можно определить следующим образом:
. (11)
Поскольку для каждой сети VPN известны свои матрицы запросов, проводя тензорный анализ характеристик для каждой VPN сети по отдельности, тем самым получив столько систем уравнений типа (11), сколько существует сетей VPN, затем просуммировав одноименные строки всех уравнений, получается финальная система уравнений, отражающая зависимость интенсивностей потоков в каждом канале связи от загрузок, создаваемых каждой отдельной сетью VPN. Таким образом, если число сетей VPN равно N, то окончательная система уравнений, определяющая потоки всех VPN сетей в каждой ветви исследуемой сети будет следующей:
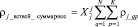, (12)
где ρj_qp – вектор узловых загрузок, создаваемых p-м сайтом q-ой VPN сети.
Система уравнений (12) содержит n уравнений, где n – число ветвей в анализируемой сети, а число неизвестных равно S•p, где S – общее число сайтов всех VPN сетей. Следовательно, система уравнений (12) имеет бесконечное число решений; это связано с тем, что каждое решение системы уравнений определяет какой-либо маршрут прохождения трафика между сайтами VPN сетей, а поскольку вариантов прохождения маршрутов существует бесконечное множество, то и система уравнений имеет бесконечное число решений. Систему уравнений (12) можно использовать для анализа трафика VPN двумя способами. Во-первых, из того, что в системе (12) загрузки в каждой ветви выражаются через линейно независимые интенсивности поступления, поэтому, определив потоки/загрузки только в линейно независимых ветвях, автоматически определяются и потоки/загрузки в оставшихся ветвях. Второй вариант использования системы уравнений (12) заключается в поиске какого-либо решения, а не в подборе значений линейно независимых компонент, при этом полученное решение будет описывать маршруты между сайтами VPN, но при таком подходе система уравнений (10) должна решаться с рядом обязательных ограничений в виде системы неравенств. Обязательными ограничениями для сиcтемы уравнений (12) являются неотрицательность потоков создаваемой отдельным сайтом q-й VPN сети, значение суммарного потока в канале связи не должно превышать величину пропускной способности данного канала, величина потока в ветви n от p-го сайта q-й VPN не должна превышать величину потока, создаваемую p-м сайтом q-й VPN сети, а также обеспечить отсутствие появления петлевых маршрутов. Дополнительными ограничениями, накладываемыми на систему уравнений (10), могут быть ограничения сквозной задержки или вероятности потерь каждого типа трафика, создаваемого сайтами VPN сетей.
Таким образом, решая систему уравнений (12) с учетом неотрицательности потоков или другими ограничениями, накладываемыми на качество обслуживания потоков сетей VPN, а также учитывая значения матриц запросов, можно однозначно формировать маршруты прохождения трафика между сайтами VPN сетей. В свою очередь если решение системы уравнений (12) совместно с накладываемыми ограничениями найти не удается, то это означает, что объем передаваемых данных превышает пропускную способность данной сети.
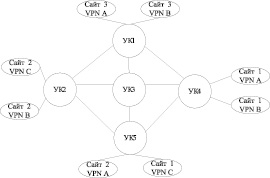
Рис. 4. Пример организации сети VPN
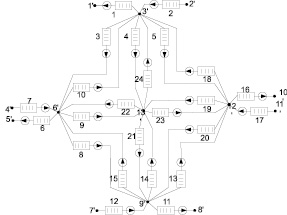
Рис. 5. Сеть массового обслуживания для исследуемой сети
Численные результаты
В качестве примера проведем анализ сети VPN, приведенной на рис. 4.
На рис. 4 УК – это узел коммутации, в роли которого, как правило, выступают маршрутизаторы или коммутаторы.
Сеть массового обслуживания, как математическая модель анализируемой сети, будет иметь вид, представленный на рис. 5.
В соответствии с ортогональным методом анализа определяется тензор преобразования от структуры исследуемой сети к структуре примитивной сети, который связывает узловые и контурные интенсивности исследуемой сети с узловыми и контурными интенсивностями примитивной формулы (8). Затем по формулам (9) и (10) определяются фазовые загрузки и фазовые интенсивности обслуживания. После чего по формуле (11) находим загрузки в каждой ветви, создаваемой p-м сайтом q-й VPN, далее по формуле (12) вычисляем загрузки в каждой ветви, создаваемые всеми сайтами.
В качестве исходных данных определим матрицы запросов как
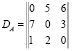Матрица запросов для сайтов VPN A;
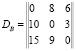Матрица запросов для сайтов VPN B;
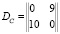Матрица запросов для сайтов VPN C.
Время обслуживания одной единицы информации приято как 0,01 с или 100 пакетов в секунду. Одним из решений системы уравнений (12) с учетом ограничений, что значения элементов векторов Pij и Pветвей должны находится в диапазоне [0;1), соответствует следующее распределение загрузок по ветвям:
.
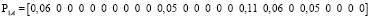
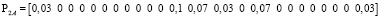
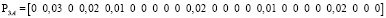
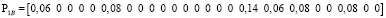
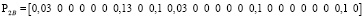
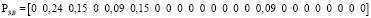
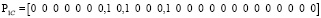
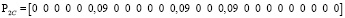Каждый вектор показывает, какая загрузка в ветвях создается p-м сайтом VPN_q. Суммарный вектор загрузок для каждой ветви показан ниже:
Pветвей =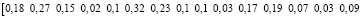 
.
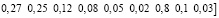Таким образом, было получено распределение трафика по каналам связи с помощью ортогонального метода, удовлетворяющее поставленной задаче, при этом необходимо отметить, что это одно из множества решений.
Заключение
В данной статье был представлен ортогональный метод формирования математической модели сетей VPN. Отличительной особенностью данного метода анализа является то, что сеть не надо приводить ни к узловому, ни к контурному виду, как это делается при контурном или узловом методе анализа. В связи с тем, что сетевая структура многих организаций строится именно на базе сетей VPN, провайдеры, предоставляющие данный вид услуг, должны обеспечивать гарантии по качеству обслуживания потоков трафика для каждой VPN. Большое количество поддерживаемых сайтов VPN и разветвленная инфраструктура сети провайдера делает задачу управления потоками трафика достаточно сложной, в свою очередь предложенный метод анализа очень хорошо описывает распределения трафика в больших системах благодаря хорошо формализованному матричному математическому аппарату, который остается инвариантным к размеру исследуемой топологии. Также необходимо отметить, что арифметические операции, производимые над матрицами, являются хорошо распараллеливаемыми вычислительными операциями, что позволит на многопроцессорных системах сократить время анализа сетей VPN. Преимуществами данного подхода по сравнению с существующими методами является простота получения математической модели, сложность вычисления маршрутов между сайтами VPN растет линейно с увеличением числа каналов в сети провайдера, в случае если необходимо провести анализ возможности организации маршрута по конкретным ветвям сети. Но если стоит задача в поиске произвольного маршрута, который будет являться решением системы уравнения (12), то накладываемое ограничение на отсутствие маршрутных петель в каждом маршруте между сайтами VPN увеличивает сложность задачи. Также необходимо отметить, что вид тензора преобразования фазовых переменных определяется матрицей разрезов и контуров исследуемой сети.
Библиографическая ссылка
Гутковская О.Л., Пономарев Д.Ю. ОРТОГОНАЛЬНЫЙ МЕТОД АНАЛИЗА СЕТЕЙ VPN // Современные наукоемкие технологии. – 2016. – № 7-1. – С. 30-37;URL: https://top-technologies.ru/ru/article/view?id=36057 (дата обращения: 23.11.2024).