Отклонение от прямолинейности является одним из видов отклонений формы. Существуют следующие разновидности отклонений от прямолинейности: отклонение от прямолинейности в плоскости, отклонение от прямолинейности оси в пространстве и отклонение от прямолинейности оси в заданном направлении.
Отклонение от прямолинейности в плоскости – наибольшее расстояние Δ от характерных точек (выступов и впадин) реального профиля до прилегающей прямой в пределах длины нормируемого участка. Частными видами отклонения от прямолинейности являются выпуклость и вогнутость.
Отклонение от прямолинейности оси в пространстве – наименьшее значение диаметра цилиндра, внутри которого располагается реальная ось поверхности вращения в пределах нормируемого участка.
Отклонение от прямолинейности оси в заданном направлении – наименьшее расстояние между двумя параллельными плоскостями, перпендикулярными к плоскости заданного направления, в пространстве между которыми располагается реальная ось в пределах нормируемого участка.
В процессе эксплуатации различных приборов внешним воздействиям в первую очередь подвергаются поверхности деталей. Износ трущихся поверхностей, смятие, коррозионное разрушение – это процессы, протекающие на поверхности деталей. Придание поверхностям деталей специальных свойств способствует существенному повышению показателей качества приборов. Качество поверхности – это совокупность всех служебных свойств поверхностного слоя материала. В соответствии с современными представлениями качество поверхностного слоя является сложным комплексным понятием и определяется двумя группами характеристик: физико-химическими и геометрическими.
Геометрические характеристики качества поверхности в порядке уменьшения их абсолютных величин следующие: отклонение формы, волнистость, шероховатость. В отдельных случаях волнистость может быть больше погрешности формы, а шероховатость больше волнистости. Волнистость занимает промежуточное положение между шероховатостью и погрешностями формы поверхности. Шероховатость поверхности не включается в отклонение формы, хотя в обоснованных случаях допускается нормировать отклонение формы, включая шероховатость поверхности. В обоснованных случаях допускается нормировать отдельно волнистость поверхности или отклонение формы без учета волнистости. Однако сложность решения задач, связанных с нормированием, технологическим обеспечением и контролем геометрических параметров реальных поверхностей, состоит в том, что их (отклонение формы, волнистость и шероховатость) весьма трудно выделить в отдельности. В реальных поверхностях обычно встречаются их комбинации.
При невысоких требованиях к точности измерения отклонения от прямолинейности применяют способ измерения прямолинейности профиля с помощью лекальной линейки, когда величину отклонения от прямолинейности оценивают по величине просвета между поверхностью лекальной линейки и измеряемой поверхностью.
Известен шаговый метод измерения прямолинейности поверхности, использующий фотоэлектрический автоколлиматор, позволяющий определять прямолинейность поверхности по углам наклона зеркала, установленного на опоре с известной базовой длиной. Последовательно перемещая опору на расстояния, равные базовой длине, и фиксируя углы наклона зеркала, строят профиль поверхности и определяют отклонение от прямолинейности [1, 2].
Измерить отклонение от прямолинейности поверхности можно, если использовать лазерный измеритель, принцип работы которого заключается в следующем: пучок излучения от оптического источника с частотой ν, предварительно расширенный афокальной трубкой, проходит светоделитель и попадает в интерферометр, где делится на два пучка – опорный и информационный [6]. Информационный пучок при отражении от движущего уголкового отражателя получает приращение частоты ± νд. В интерферометре информационный пучок соединяется с опорным пучком.
Большинство информационно-измерительных систем при использовании оптической схемы с акустооптическим преобразованием после модуляции работает по схеме Майкельсона [2, 3]. Применение лазеров в информационно-измерительных системах повышает точность измерений, в первую очередь, благодаря увеличению контрастности и сужению интерференционных полос. Схема с акустооптическим преобразованием до модуляции сигнала обладает большей помехоустойчивостью (более высоким соотношением «сигнал/шум» на выходе схемы), чем схема с акустооптическим преобразованием после модуляции. Поэтому контраст интерферирующих полос при использовании этой схемы выше.
В модуляторе оба пучка дифрагируют на n максимумов. Частота излучения в n-ом максимуме равна ν ± nF, где n = 0, ± 1, ± 2,…, т.е. сдвинута относительно частоты исходного излучения ν на величину, кратную частоте ультразвуковой волны F0. Первый дифракционный порядок опорного пучка совмещен оптической схемой с нулевым дифракционным порядком информационного пучка.
На фотоприемник действуют излучения двух частот ν ± Δfд и Δ ± F0. С фотоприемника снимается сигнал разностной частоты F ± Δfд, в котором заключена информация о перемещении подвижного отражателя. О величине контролируемого перемещения судят по сдвигу фазы информационного сигнала относительно опорного сигнала.
Для проведения операции контроля прямолинейности направляющих необходимо, чтобы лазерный измеритель имел два измерительных канала. При этом один канал работает в режиме линейных измерений, а второй – в режиме угловых [4]. Отражатель, служащий для линейных измерений, и блок отражателей для угловых измерений устанавливают на общую каретку. Каретку перемещают вдоль линии измерений на величину выбранного шага, измеренного с помощью канала, работающего в режиме линейных измерений. Второй канал, работающий в режиме угловых измерений, даст величину угла на данном шаге.
Оптическая схема интерферометра для измерения линейных перемещений показана на рис. 1. Отражатель в одном плече интерферометра устанавливается на контролируемый объект, и по результатам измерения фазы φ вычисляют величину перемещения объекта по формуле [5]:
L = φλд, (1)
где φ – накопленная за время измерения (движения) фазовая разность хода интерферирующих световых волн; λд – действительная длина волны оптического излучения.
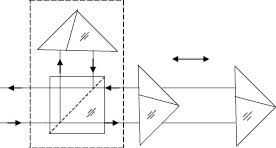
Рис. 1. Схема для измерения линейных перемещений объекта
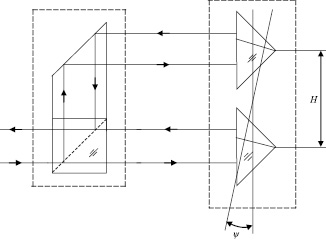
Рис. 2. Схема для измерения угловых перемещений объекта
На рис. 2 представлена оптическая схема интерферометра для измерения угловых перемещений. При повороте блока отражателей, закрепленных на объекте, на угол ψ возникает разность геометрических длин в обоих плечах интерферометра, что приводит к изменению фазы интерференционного сигнала Δφ. Величина угловых перемещений рассчитывается по формуле [5]:
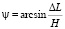, (2)
где ΔL – изменения оптического хода двух измерительных интерферирующих световых пучков.
Изменение оптического пути луча в отражателе при развороте последнего на угол y показано на рис. 3.
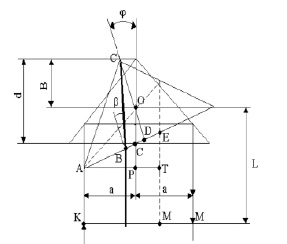
Рис. 3. Схема изменения оптического пути в отражателе при его повороте
При повороте отражателя на угол ψ оптический путь луча Δ будет складываться из следующих составляющих:
,
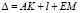где АК – путь луча на участке от поверхности КМ до точки А входа луча в отражатель; l – путь луча в отражателе; ЕМ – путь луча от точки выхода луча из отражателя до плоскости КМ.
В свою очередь,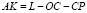 
.
Из треугольника СОD: OC = (d – b)sec(ψ).
Из треугольника АСР: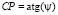 
.
Соответственно AK = L – (d – b)sec(ψ) – atg(ψ).
Отрезок ЕМ равен EM = L – OC – CP + TE.
Из треугольника АТЕ: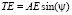 
.
Положение точки В на фронтальной грани отражателя определяется местом входа центрального луча, для которого точки входа и выхода совпадают между собой. Центральный луч после преломления на фронтальной грани проходит через вершину отражателя С и возвращается по тому же направлению. Отрезок АВ найдем из следующего соотношения:
,
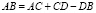где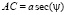 
(из треугольника АСР), 
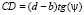(из треугольника СОD), 
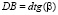(из треугольника ВСD).
Подставляя АС, СD и DВ в выражение для АЕ, получим
.
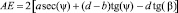Следовательно, отрезок ТЕ будет равен
.
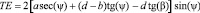Из полученного выражения следует, что изменения оптического пути D при повороте отражателя на угол y относительно центра вращения О равны
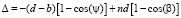. (3)
Если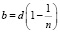 
и пренебречь членами по y выше второго порядка, то D = 0.
На рис. 4 представлена функциональная схема для измерения угловых величин, в которой уголковые отражатели расположены друг за другом. При движении каретки с блоком отражателей по измеряемой поверхности в случае непрямолинейности измеряемой поверхности блок отражателей совершает наклоны, что приводит к изменению длины оптического хода волн. Изменение разности хода пучков волн приводит к изменению фазы электрического сигнала, которое пропорционально непрямолинейности измеряемой поверхности.
Отклонение от прямолинейности на шаге m вдоль измерений от прямой, соединяющей крайние точки, в которых производились измерения, вычисляют по формуле
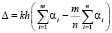, (4)
где Δ – отклонение от прямолинейности; k – числовой коэффициент, зависящий от базовых расстояний оптической схемы и длины волны оптического излучения; h – выбранный шаг измерений; i – величина угла, отсчитанного по показаниям прибора на шаге L; m – порядковый номер шага; n – общее количество шагов на измеряемом интервале.
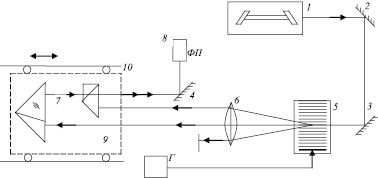
Рис. 4. Функциональная схема для измерения отклонения от прямолинейности
Геометрический расчет показывает, что разность оптического хода интерферирующих световых пучков при наклоне блока отражателей равна
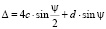, (5)
где с – расстояние между двумя уголковыми отражателями; d – расстояние между двумя оптическими пучками.
При измерении малых углов (до 2,5 °) можно пользоваться упрощенной формулой для измерения угла наклона:
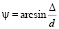. (6)
На основании (рис. 4) закреплены источник оптического излучения 1; поворотные зеркала 2, 3, 4; акустооптический модулятор 5; система линз 6; оптический блок 7; фотоприемник 8. Оптический блок 7 закреплен на каретке 9, которая движется по направляющим 10. В оптическом блоке, расположенном на подвижной каретке, происходит интерференция двух измерительных разночастотных световых пучков, разность оптических ходов которых отображает угловые наклоны оптического блока относительно средней линии перемещения. Измерительный сигнал, который возникает при изменении оптического хода одного измерительного пучка относительно другого в результате угловых перемещений каретки при движении ее, подается на фотоприемник 8. С фотоприемника электрический измерительный сигнал, несущий информацию о пространственных наклонах каретки, подается в блок индикации.
Приведенное выражение показывает, что функциональная зависимость изменений разности хода D от угла поворота y имеет систематическую погрешность, которая при малых углах незначительна и обычно не принимается во внимание. При увеличении диапазона измерений необходимо учитывать точность изготовления и юстировки оптических элементов.
Библиографическая ссылка
Базыкин С.Н. ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ ДЛЯ ИЗМЕРЕНИЯ ОТКЛОНЕНИЙ ОТ ПРЯМОЛИНЕЙНОСТИ ПЕРЕМЕЩЕНИЙ // Современные наукоемкие технологии. – 2016. – № 7-1. – С. 21-25;URL: https://top-technologies.ru/ru/article/view?id=36055 (дата обращения: 21.11.2024).