Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Живаева В.В. 1 Никитин В.И. 1

---

1 Самарский государственный технический университет

Радиус проникновения фильтрата бурового раствора является одним из характерных параметров загрязнения пласта. Проникновение фильтрата бурового раствора влияет на многофазное течение в пористой среде. Рассмотрена задача о фильтрации бурового раствора через глинистую корку, с расчетом полного объёма фильтрата, проникшего в пласт. Методами математического моделирования выведены уравнения, соответствующие фильтрационным процессам при двухфазной фильтрации в пластовых условиях. В данной работе представлен алгоритм расчета радиуса проникновения фильтрата бурового раствора при вскрытии пласта-коллектора. Результаты применения данной модели можно использовать при выборе рецептуры бурового раствора. Полученные результаты полностью соответствуют физической постановке задачи. На основании анализа уравнений, используемых в данной работе, даны рекомендации по технологии вскрытия продуктивного пласта.

Статья в формате PDF

0 KB

радиус проникновения

фильтрационная корка

буровой раствор

двухфазная фильтрация

алгоритм расчета

математическая модель

1. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. – М., 1984. – 211 с.

2. Белозеров И.П., Юрьев А.В. Определение относительных фазовых проницаемостей на образцах полноразмерного керна // Молодая нефть: сб. статей. Всерос. молодежной науч.-техн. конф. нефтегазовой отросли / отв. за выпуск О.П. Калякина. – Красноярск: Сиб. федер. ун-т, 2014.

3. Никитин В.И., Живаева В.В. Вероятные пути решения проблем вскрытия напряжённых горных пород // Ашировские чтения: cб. трудов Международной научно-практической конференции. Т. 1. – Самара: Самар. гос. техн. ун-т, 2014. – С. 148–149.

4. Никитин В.И., Живаева В.В. Применение методов математического моделирования для управления свойствами буровых растворов // Ашировские чтения: сб. трудов Международной научно-практической конференции. – Самара: Самар. гос. техн. ун-т, 2015. – С. 81–85.

5. Jr. Adam T. Bourgoyne, Keith K. Millheim, Martin E. Chenevert, Jr. F.S. Young. – Second Printing. – Society of Petroleym Engineers Richardson, TX, 1991. – 508 p.

6. Kegang Ling A New Approach To Estimate Invasion Radius of Water-Based-Drilling-Fluid Filtrate To Evaluate Formation Damage Caused by Overbalanced Drilling. – SPE Drilling & Completion Publisher: Society of Petroleum Engineers, 2015. – P. 27–36.

Одним из основных факторов, влияющих на состояние прискважинной зоны пласта, является физико-химическое воздействие на него бурового раствора при первичном вскрытии. Проникновение в эту зону промывочной жидкости или её фильтрата вызывает изменение фильтрационно-ёмкостных свойств продуктивного пласта, в результате чего вокруг скважины образуется зона с пониженной, по сравнению с естественной, проницаемостью [3]. Оценка количественных изменений фильтрационных параметров пород призабойной зоны пласта после проникновения фильтрата бурового раствора позволяет правильно выбирать состав раствора и предупреждать возможные осложнения в процессах дальнейшей эксплуатации скважин. Одним из характерных параметров загрязнения продуктивного пласта является радиус проникновения фильтрата бурового раствора. В данной работе предложена методика оценивания радиуса проникновения фильтрата в пласт. Результаты применения данной модели следует использовать при выборе рецептуры бурового раствора с целью снижения загрязнения призабойной зоны [4].

Моделирование фильтрации бурового раствора через глинистую корку

Общий объём проникнувшего в пласт фильтрата бурового раствора зависит от характерного времени процесса, перепада давлений, вязкости фильтрата и пластового флюида, проницаемости пласта и толщины глинистой корки [5]. Опыты показывают, что спустя некоторое время tconst толщина корки становится постоянной, и тогда весь процесс фильтрации можно разделить на мгновенную фильтрацию, фильтрацию при росте глинистой корки и фильтрацию через корку постоянной толщины.

Мгновенную фильтрацию можно приближённо рассчитать из статических/динамических исследований фильтрационных свойств бурового раствора. Справедлива следующая пропорция:

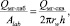(1)

где Qмг-лаб – мгновенная фильтрация, полученная на фильтр-прессе; Qмг-скв – мгновенная фильтрация в скважине; Alab – площадь фильтрации при испытании на фильтр-прессе; rw – радиус скважины; h – мощность пласта.

Скорость фильтрации бурового раствора через глинистую корку можно описать законом Дарси и вычислить как

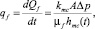(2)

где k_mc – проницаемость глинистой корки; Δp – перепад давлений через глинистую корку; h_mc(t) – толщина корки, растущая со временем; q_f – скорость фильтрации.

Через некоторое время t, после начала фильтрации, объём твёрдых частиц отфильтрованного бурового раствора равняется объёму твёрдых частиц, осаждённых на фильтрационной корке:

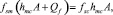(3)

где f_sc – объёмная доля твёрдых частиц в глинистой корке; f_sm – объёмная доля твёрдых частиц в растворе. Тогда проинтегрировав (2) с учетом (3), получим формулу для расчёта объёма фильтрата при росте глинистой корки:

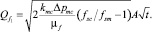(4)

Чтобы вычислить объём фильтрата при постоянной толщине корки, уравнение (2) проинтегрируем при h_mc(t) = h_mсconst:

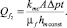(5)

В качестве толщины корки можно взять разность между радиусом скважины и размером долота, взятого из кавернограммы, или толщину корки, установленную экспериментальным путём. Тогда из (3) и (4) можно выразить время tconst, необходимое для образования корки постоянной толщины h_mсconst:

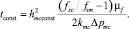(6)

Чтобы рассчитать полный объём фильтрата, проникшего в ПЗП, необходимо просуммировать (1), (4), (5):

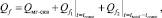(7)

где t_total – общее время фильтрационного процесса.

Средняя скорость фильтрации вычисляется как отношение полного объёма фильтрата ко времени фильтрационного процесса:

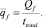(8)

При использовании формулы (7) для вычисления общего объёма фильтрата, в случае изменения давления репрессии, необходимо разбивать временные интервалы на участки, в которых давление постоянно, и вести расчёты, применив соответствующие преобразования.

Расчет радиуса проникновения фильтрата бурового раствора в пласт с использованием моделей относительных фазовых проницаемостей

Пренебрегая капиллярным давлением, для высокопроницаемых пластов функция распределения потоков фаз [1] имеет вид

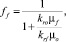(9)

где k_rf, k_ro, μ_f, μ_o – относительные фазовые проницаемости и динамические вязкости для фильтрата и для нефти соответственно.

Функцию f_f называют функцией Баклея – Леверетта. Функция f_f = f_f(S_f) является функцией от насыщенности S_f и представляет собой отношение скорости фильтрации вытесняющей фазы q_f (фильтрата) и суммарной скорости фильтрации q_t, равна объемной доле фильтрата в суммарном потоке двух фаз. Эта функция определяет полноту вытеснения и характер распределения насыщенности фильтратом по пласту.

Для расчёта радиуса загрязнённой зоны пласта используем следующую формулу [6]:

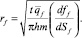(10)

Для использования формулы (10) необходимо иметь параметры, вошедшие в неё. Временной промежуток t рекомендуется отсчитывать от момента первоначального проникновения в пласт до начала цементирования. Пористость m можно определить, например, из анализа керна или геофизических исследований скважины, h – мощность пласта. df_f/dS_f определяется через относительные проницаемости и свойства жидкости. Относительные проницаемости могут быть получены из лабораторных исследований. Также существуют модели, которые можно использовать при отсутствии сведений о лабораторных исследованиях. Фактически модели относительных фазовых проницаемостей являются аппроксимациями эмпирических данных [2].

Рассчитав среднюю скорость проникновения фильтрата в пласт, пользуясь формулой (10), можно рассчитать радиус проникновения фильтрата в пласт при плоско-радиальном течении а также распределение насыщенности горной породы. Для того, чтобы пользоваться выведенными формулами, необходимо обсудить функцию f_f = f_f(S_f), так как её производная dff/dSf входит в расчётные уравнения. Данная функция зависит от фазовой проницаемости, поэтому для дальнейшего решения поставленной задачи следует указать параметры, характеризующие двухфазный фильтрационный процесс.

Определить относительные фазовые проницаемости можно на образцах керна, при лабораторных исследованиях или воспользоваться имеющимися моделями, применимыми для данной задачи. Рассматривая задачу о проникновении фильтрата бурового раствора на водной основе, воспользуемся эмпирическими формулами Чень-Чжун-Сян для относительных фазовых проницаемостей для воды и нефти:

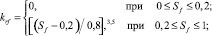
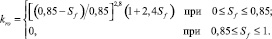(11)

В данном предположении фильтрат бурового раствора близок по своим характеристикам к воде. Тогда, подставляя данные выражения в (2), запишем функцию Баклея – Леверетта:

f_f = 0, при 0 ≤ S_f ≤ 0,2;

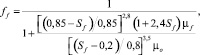при 0,2 ≤ S_f ≤ 0,85; (12)

f_f = 1, при 0,85 ≤ S_f ≤ 1.

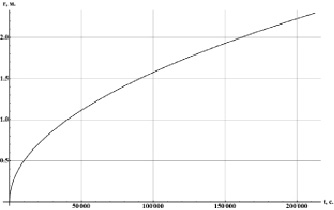
Зависимость радиуса проникновения фильтрата в ПЗП от времени

Производная df_f/dS_f на интервалах 0 ≤ S_f ≤ 0,2; 0,85 ≤ S_f ≤ 1 не определена, а на интервале 0,2 ≤ S_f ≤ 0,85 вычисляется дифференцированием по S_f.

Таким образом, используя (10), можно построить зависимость радиуса проникновения фильтрата от времени. Для этого необходимо для каждого промежутка времени t определить объём проникшего фильтрата, среднюю скорость фильтрации и далее, используя dff/dSf, построить график зависимости радиальной координаты r от t. Пример такой зависимости изображен на рисунке. Стоит отметить, что аналогично можно построить зависимость насыщенности породы от радиальной координаты r.

Поскольку df_f/dS_f достаточно сложным образом зависит от Sf, то нахождение точки экстремума этой функции методами математического анализа является затруднительным. В случае параболического распределения задача легко решается графически. При использовании более простых математических моделей относительных фазовых проницаемостей целесообразно находить максимум функции dff/dSf методами математического анализа. Также для алгоритмичности решения данной задачи можно использовать численные методы нахождения экстремума функции.

Алгоритм расчета радиуса проникновения

Последовательность вычислений:

1. Рассчитать мгновенную фильтрацию бурового раствора по формуле (1).

2. Разделить период фильтрации на несколько временных интервалов. Давление репрессии должно быть постоянным в каждом интервале.

3. Вычислить время образования глинистой корки постоянной толщины по формуле (6) (либо использовать значение, заданное технологическими условиями).

4. Рассчитать объем фильтрата по уравнению (7), с учетом всех временных интервалов.

5. Используя полученный результат, вычислить среднюю скорость фильтрации по формуле (8).

6. Построить модель относительных фазовых проницаемостей для нефти и для фильтрата бурового раствора или выбрать подходящую из существующих.

7. Используя модель относительных фазовых проницаемостей, построить функцию Баклея – Леверетта f_f и её производную df_f/dS_f.

8. Определить максимум функции df_f/dS_f.

9. Используя результаты предыдущих пунктов, вычислить радиус проникновения бурового раствора в пласт по формуле (10).

Входные параметры задачи:

kmc – проницаемость глинистой корки;

h – мощность пласта;

μ_f – вязкость фильтрата бурового раствора;

μo – вязкость нефти в пластовых условиях;

f_sc – объёмная доля твердых частиц в корке;

f_sm – объёмная доля твердых частиц в буровом растворе;

m – пористость породы;

rw – радиус скважины;

Δp – давление репрессии;

k_rf – относительная фазовая проницаемость для фильтрата бурового раствора;

k_ro – относительная фазовая проницаемость для нефти;

A_lab – площадь фильтрации на фильтр-прессе;

h_const – постоянная толщина глинистой корки;

Q_мг-лаб – объём мгновенной фильтрации на фильтр-прессе;

t_total – полное время фильтрации;

t_const – время образования корки постоянной толщины.

Вывод

При проведении расчётов по предложенному алгоритму стоит отметить, что большое количество входных параметров задачи является необходимостью с технической точки зрения, так как рассмотренная задача учитывает процессы, протекающие в следующей системе: «буровой раствор – глинистая корка – фильтрация в пористой нефтенасыщеной среде». Поэтому результат вычислений зависит от совокупности факторов.

Следует отметить, что необходимо ставить задачу по уменьшению объёма отфильтрованной в ПЗП жидкости, за счёт ее реологических свойств и доли твёрдой фазы. Особое внимание стоит уделить проницаемости и толщине фильтрационной корки. При высокой проницаемости глинистой корки значительное количество жидкости может проникнуть в пласт за меньшее время фильтрации, что явно видно из анализа уравнений фильтрации. Повышенное давление репрессии также вносит существенный вклад в увеличение объёма потерянной жидкости. При этом следует помнить, что поддерживаемое давление должно в достаточной мере превосходить пластовое, но не превышать давление гидроразрыва. В противном случае неизбежными последствиями будут проникновение большого количества фильтрата в поровое пространство и ухудшение фильтрационно-ёмкостных свойств пласта-коллектора. Следовательно, плотность бурового раствора должна быть выбрана в соответствии с регламентированным перепадом давлений. Рецептура бурового раствора должна быть выбрана таким образом, чтобы фильтрация в пласт была минимальна.

На основании анализа уравнений, используемых в данной работе, можно дать следующие рекомендации по технологии вскрытия продуктивного пласта. Путём снижения средней скорости фильтрации бурового раствора ожидаемо уменьшение радиуса проникновения бурового раствора в пласт. Для этого требуется снижение проницаемости фильтрационной корки за счёт физико-химических характеристик бурового раствора. Вскрытие продуктивного пласта следует производить при минимально допустимом давлении репрессии, либо возможно его снижение во время простоя скважины. Время вскрытия пласта и простоя скважины также влияет на глубину проникновения бурового раствора.

Библиографическая ссылка