Известно [3], что для передачи M-буквенного сообщения (где М считается достаточно большим) по линии связи, допускающей m различных элементарных сигналов, требуется затратить 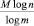 сигналов, где n – число букв «алфавита», с помощью которого записано сообщение. Так как кабардино-черкесский «телеграфный» алфавит содержит 33 буквы (мы здесь не различаем буквы е и ё, ь и ъ, которые в большинстве телеграфных кодов передаются одной и той же комбинацией элементарных сигналов, но причисляем к числу букв и «нулевую букву» – пустой промежуток между словами и букву I), то согласно этому результату на передачу M-буквенного сообщения надо затратить
сигналов, где n – число букв «алфавита», с помощью которого записано сообщение. Так как кабардино-черкесский «телеграфный» алфавит содержит 33 буквы (мы здесь не различаем буквы е и ё, ь и ъ, которые в большинстве телеграфных кодов передаются одной и той же комбинацией элементарных сигналов, но причисляем к числу букв и «нулевую букву» – пустой промежуток между словами и букву I), то согласно этому результату на передачу M-буквенного сообщения надо затратить 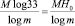 элементарных сигналов. Здесь H0 = log233 = 5,044394118 – энтропия опыта, заключающегося в приеме одной буквы кабардино-черкесского текста (информация, содержащаяся в одной букве), при условии, что все буквы считаются одинаково вероятными. На самом деле, однако, появление в сообщении на кабардино-черкесском языке разных букв совсем не одинаково вероятно. Для получения текста, в котором каждая буква содержит 5,044394118 бит информации, нельзя просто взять отрывок из какой-либо книги на кабардинском языке; для этого требуется выписать 33 буквы на отдельных билетиках, сложить все эти билеты в урну и затем вытаскивать их по одному, каждый раз записывая вытянутую букву, а билетик возвращая обратно в урну и снова перемешивая ее содержимое. Произведя такой опыт, мы придем к «фразе» вроде следующей:
элементарных сигналов. Здесь H0 = log233 = 5,044394118 – энтропия опыта, заключающегося в приеме одной буквы кабардино-черкесского текста (информация, содержащаяся в одной букве), при условии, что все буквы считаются одинаково вероятными. На самом деле, однако, появление в сообщении на кабардино-черкесском языке разных букв совсем не одинаково вероятно. Для получения текста, в котором каждая буква содержит 5,044394118 бит информации, нельзя просто взять отрывок из какой-либо книги на кабардинском языке; для этого требуется выписать 33 буквы на отдельных билетиках, сложить все эти билеты в урну и затем вытаскивать их по одному, каждый раз записывая вытянутую букву, а билетик возвращая обратно в урну и снова перемешивая ее содержимое. Произведя такой опыт, мы придем к «фразе» вроде следующей:
хаы ьаоружс 1ьцкяпажзфжичербжижкиюжжайэтцьы ыхшзэаю1ецфшйкжт чевпыкпбуьйхцсеытадшевдэ1ющйээгхп
Этот текст, хоть он и составлен из букв кабардинского алфавита, имеет мало общего с кабардинским языком!
Для более точного вычисления информации, содержащейся в одной букве кабардинского текста, надо знать вероятности появления различных букв. Эти вероятности можно определить, взяв достаточно большой отрывок, написанный на кабардинском языке, и рассчитав для него относительные частоты отдельных букв. Строго говоря, эти частоты могут несколько зависеть от характера текста; поэтому для надежного определения «средней частоты» буквы желательно иметь набор различных текстов, заимствованных из различных источников.
Таблица 1
Таблица частот букв кабардинских тексов
|
Буква Относительная частота |
- 0,133 |
Э 0,114 |
Ы 0,069 |
Ъ,Ь 0,068 |
У 0,064 |
А 0,054 |
Р 0,039 |
1 0,047 |
|
Буква Относительная частота |
Х 0,038 |
К 0,037 |
Щ 0,037 |
И 0,036 |
М 0,034 |
З 0,019 |
Г 0,022 |
Ж 0,022 |
|
Буква Относительная частота |
Н 0,019 |
T 0,019 |
Д 0,018 |
Л 0,017 |
Б 0,015 |
П 0,015 |
Е,Ё 0,014 |
С 0,014 |
|
Буква Относительная частота |
О 0,006 |
Ф 0,006 |
Й 0,005 |
Я 0,005 |
Ш 0,005 |
Ц 0,003 |
В 0,002 |
Ч 0,002 |
|
Буква Относительная частота |
Ю 0,000 |
В качестве исследуемых текстов были взяты национальные произведения А.Т. Шортанова «Къэзэнокъуэ Жэбэгъы», Б.М. Карданова «Бжьыхьэ жэщым», А.А. Шогенцукова «Нанэ». Получена следующая таблица частот:
Исследование состояло в непосредственном подсчете H0 и H1 – энтропий нулевого и первого порядка приближения – и нахождения верхних оценок Hn для энтропий порядка приближения n. При этом графемы кабардинского языка разлагались на составные элементы. Таким образом, считалось, что алфавит, с помощью которого составлен текст, содержит 33 буквы (31 буква русского языка, буква I и пробел). Поэтому H0 оказалось равным log233 ~ 5,044394118. H1 подсчитывалась обычным образом с помощью таблицы частот букв (табл. 1), составленной на основе исследования указанных выше текстов.
Приравняв эти частоты к вероятностям появления соответствующих букв, получим для энтропии одной буквы кабардинского текста приближенное значение:
H1 = –0,133log0,133 – 0,114log0,114 – 0,069log0,069 – … – 0,002log0,002 ~ ~ 4,463793204 бит.
Из сравнения этого значения с величиной H0 = log233 = 5,044394118 видно, что неравномерность появления различных букв алфавита приводит к уменьшению информации, содержащейся в одной букве кабардинского текста, примерно на 0,580600914 бит.
Воспользовавшись этим обстоятельством, можно уменьшить число элементарных сигналов, необходимых для передачи М-буквенного сообщения до значения 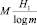 (т.е. в случае двоичного кода – до значения H1M ≈ 4,463793204).
(т.е. в случае двоичного кода – до значения H1M ≈ 4,463793204).
Но и равное 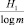 значение среднего числа элементарных сигналов, приходящихся на одну букву передаваемого сообщения, также не является наилучшим. В самом деле, при определении энтропии H1 = H(α1) опыта α1, состоящего в определении одной буквы кабардинского текста, мы считали все буквы независимыми. Это значит, что для составления «текста», в котором каждая буква содержит H1 = 4,463793204 бит информации, мы должны прибегнуть к помощи урны, в которой лежат тщательно перемешанные 1000 бумажек, на 133 которых не написано ничего, на 114 – написана буква Э, на 69 – ы,…, наконец, на 2 бумажках – буква ч. Извлекая из такой урны бумажки по одной, придем к «фразе» вроде следующей:
значение среднего числа элементарных сигналов, приходящихся на одну букву передаваемого сообщения, также не является наилучшим. В самом деле, при определении энтропии H1 = H(α1) опыта α1, состоящего в определении одной буквы кабардинского текста, мы считали все буквы независимыми. Это значит, что для составления «текста», в котором каждая буква содержит H1 = 4,463793204 бит информации, мы должны прибегнуть к помощи урны, в которой лежат тщательно перемешанные 1000 бумажек, на 133 которых не написано ничего, на 114 – написана буква Э, на 69 – ы,…, наконец, на 2 бумажках – буква ч. Извлекая из такой урны бумажки по одной, придем к «фразе» вроде следующей:
уэтбдъ утлижы яэкр ужегык мщйхты хысыъш оиаэшм.
Эта «фраза» несколько более похожа на осмысленную кабардинскую речь, чем предыдущая (здесь все же наблюдается сравнительно правдоподобное распределение числа гласных и согласных и близкая к обычной средняя длина «слова»), но и она, разумеется, еще очень далека от разумного текста.
Несходство нашей фразы с осмысленным текстом, естественно, объясняется тем, что на самом деле последовательные буквы кабардинского текста вовсе не независимы друг от друга.
Наличие в кабардинском языке дополнительных закономерностей, не учтенных в нашей «фразе», приводит к дальнейшему уменьшению степени неопределенности (энтропии) одной буквы кабардинского текста. Поэтому при передаче такого текста по линии связи можно еще уменьшить среднее число элементарных сигналов, затрачиваемых на передачу одной буквы. Для этого надо лишь подсчитать условную энтропию 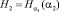 опыта α2, состоящего в определении одной буквы кабардинского текста, при условии, что нам известен исход опыта α1, состоящего в определении предшествующей буквы того же текста (заметим, что при приеме очередной буквы сообщения мы всегда знаем уже предшествующую букву). Условная энтропия H2 определяется следующей формулой:
опыта α2, состоящего в определении одной буквы кабардинского текста, при условии, что нам известен исход опыта α1, состоящего в определении предшествующей буквы того же текста (заметим, что при приеме очередной буквы сообщения мы всегда знаем уже предшествующую букву). Условная энтропия H2 определяется следующей формулой:
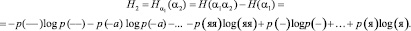
В результате подсчета этих величин с помощью программы были получены следующие результаты:
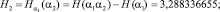
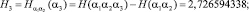
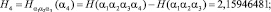
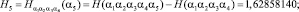
…………........................................................................................…;
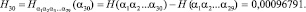
Зная величину H2, можно провести эксперимент и получить следующий результат:
ур уэтхэм ихапср к1у ахъумн нэм зышэ къэк1э
По звучанию эта «фраза» заметно ближе к кабардинскому языку, чем фраза, выписанная в первом случае.
Для H5 моделирование привело к следующему результату:
зыбжа ц1ыху хьэлэ хэкур уэста гьуэтр шэрдж бгыры.
Среднее число элементарных сигналов, необходимое для передачи одной буквы текста, не может быть меньшим 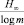 ; с другой стороны, возможно кодирование, при котором это среднее число сколь угодно близко к величине
; с другой стороны, возможно кодирование, при котором это среднее число сколь угодно близко к величине 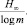 Разность
Разность 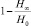 , показывающую, насколько меньше единицы отношение «предельной энтропии» H∞ к величине H0 = log n, характеризующей наибольшую информацию, которая может содержаться в одной букве алфавита с данным числом букв, Шеннон назвал избыточностью языка. В нашем случае имеем следующий результат:
, показывающую, насколько меньше единицы отношение «предельной энтропии» H∞ к величине H0 = log n, характеризующей наибольшую информацию, которая может содержаться в одной букве алфавита с данным числом букв, Шеннон назвал избыточностью языка. В нашем случае имеем следующий результат:
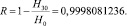
Такая избыточность языка позволяет сокращать телеграфный текст за счет отбрасывания некоторых легко отгадываемых слов (предлогов и союзов); она же позволит легко восстановить истинный текст даже при наличии значительного числа ошибок в телеграмме или описок в книге.
Избыточность R является весьма важной статистической характеристикой языка. Для сравнения результатов, полученных для кабардинского языка, приведем значения энтропий некоторых европейских языков (табл. 2).
Таблица 2
Значения энтропии некоторых европейских языков
|
Язык |
Английский |
Немецкий |
Французский |
Испанский |
Кабардинский |
|
H1 |
4,03 |
4,10 |
3,96 |
3,98 |
4,46 |
Для английского языка Шеннон получил следующие значения энтропий (табл. 3).
Таблица 3
Значения энтропии английского языка
|
H0 |
H1 |
H2 |
H3 |
H5 |
H8 |
|
4,76 |
4,03 |
3,32 |
3,10 |
~2,1 |
~1,9 |
Для кабардинского языка мы получили следующие результаты (табл. 4).
Таблица 4
Значения энтропии кабардинского языка
|
H0 |
H1 |
H2 |
H3 |
H5 |
H8 |
|
5,04 |
4,46 |
3,28 |
2,72 |
1,62 |
0,52 |
Д.Н. Ленским в работе [1] была сделана попытка оценить энтропию адыгейских печатных текстов (табл. 5).
Таблица 5
Значения энтропии адыгейского языка
|
H0 |
H1 |
H11 |
H16 |
H21 |
H41 |
|
5,09 |
4,45 |
2,57 |
2,74 |
2,71 |
2,20 |
Таким образом, исходя из полученных Д.Н. Ленским результатов, нетрудно подсчитать избыточность печатных текстов, которая составляет 56,77 %. В связи с неидеальностью процесса отгадывания, на которое указывает сам автор получились некоторые скачки значений энтропий. Считаем, что избыточность печатных адыгейских текстов должна быть немного выше полученного значения. Опыты Шеннона [5] показали, что величина H100, по-видимому, заключена между 0,6 и 1,3 бит. И для английского языка избыточность составляет порядка 80 %. Для немецкого языка К. Кюнфмюллером [4] было получено значение – 70 %. Для французского языка избыточность была подсчитана Н.В. Петровой [2] и составила порядка 71 %.
Библиографическая ссылка
Тхамоков М.Б., Канчукоев В.З. ЭНТРОПИЯ КАБАРДИНСКОГО ПЕЧАТНОГО ТЕКСТА // Современные наукоемкие технологии. 2016. № 5-3. С. 487-490;URL: https://top-technologies.ru/ru/article/view?id=35938 (дата обращения: 09.03.2026).



