Течение заболеваний часто сопровождается множественностью симптомов, приобретающих индивидуальный характер для каждого больного из-за особенностей его состояния здоровья и проявления клинической картины. В дифференциальной диагностике главным умением является «определение кратчайшего пути от самого яркого симптома к диагнозу» [1]. Процесс принятия диагностических решений в медицине часто связан с опытом врача, его умением слушать, сопоставлять факты и делать правильные выводы. Одной из сложностей при этом выступает появление атипичных случаев течения заболеваний. Как писал Р. Ригельман: «Атипичные симптомы частых болезней бывают чаще, чем типичные симптомы редких».
В медицине знания слабо структурированы, что затрудняет применение формальной логики объективного знания и общепринятых методов анализа причин и следствий [1]. При разработке автоматизированных диагностических систем в медицине с большим успехом применяется подход, базирующийся на синтезе знаний на основе обобщения имеющихся априорных данных [2, 3, 4]. Этот подход используется в таком направлении искусственного интеллекта, как искусственные нейронные сети (ИНС).
Разработка интеллектуальных информационных систем в медицине сопровождается накоплением больших массивов данных, которые часто даже высококлассному профессионалу-эксперту просто физически невозможно проанализировать [6].
Таким образом, актуальным представляется создание программ, основанных на искусственном интеллекте, для автоматического поиска атипичных случаев, которые будут обращать внимание врача-эксперта на пограничные ситуации в дифференциальной диагностике.
Целью исследования, описанного в данной работе, является разработка системы автоматического поиска для выявления атипичных графиков авторегрессионных облаков (АРО) межпульсовых интервалов у больных с синдромом фибрилляции предсердий (ФП) на основе компьютерного моделирования самоорганизующейся искусственной нейронной сети.
Для достижения поставленной цели необходимо решить следующие задачи:
– сформировать банк примеров АРО разных классов у больных с ФП;
– разработать модель ИНС и сформировать эффективный обучающий алгоритм для решения задачи категоризации АРО больных ФП;
– выполнить апробацию разработанных моделей и алгоритмов в виде компьютерного приложения;
– проанализировать результаты решения задачи автоматической категоризации с выявлением атипичных графиков АРО при синдроме ФП.
Для решения поставленных задач была использована методология системного анализа, теории принятия решений, нейрокибернетики, теории управления и теории моделирования. Прежде всего, была разработана математическая модель ИНС и её программная реализация для выявления атипичных АРО у больных ФП.
Математическая модель ИНС для выявления атипичных АРО при синдроме ФП
Течение основного заболевания с синдромом фибрилляции предсердий часто сопровождается угрозой осложнений и подразумевает неблагоприятный отдаленный прогноз. Для выбора адекватных способов лечения ФП необходим прогноз полезности восстановления синусового ритма над риском эмболических осложнений и возможных рецидивов фибрилляции предсердий.
Одним из методов диагностики при ФП является анализ авторегрессионных облаков [5, 7]. Авторегрессионное облако является графическим изображением попарного распределения предыдущего и последующего межпульсового интервала на координатной плоскости.
Метод корреляционной ритмографии позволяет разделить полученные графики АРО больных с синдромом ФП на пять функциональных классов:
1. Мономодальный симметричный.
2. Мономодальный асимметричный.
3. Мономодальный инвертированный.
4. Полимодальный.
5. Амодальный.
На рис. 1 приведены графики разных классов АРО, которые следует разграничивать.
Класс АРО в известной мере отражает степень утраты регуляторных воздействий синусового узла на ритм сердца при ФП. При благоприятном прогнозе на восстановление синусового ритма наблюдается одно выраженное сгущение точек, что характерно для мономодальных классов. При этом отмечается достаточное сохранение регуляторных воздействий для первого класса, меньшее – при втором, наименьшее – при третьем классе. Переходной формой между трепетанием и мерцанием предсердий является четвертый класс. АРО пятого класса свидетельствуют о том, что функциональное состояние синусового узла неудовлетворительно и перспективы на восстановление правильного синусового ритма сомнительны.
Часто на АРО у больных ФП нет четких признаков принадлежности их к конкретному классу, особенно это характерно для графиков полимодального и асимметричного классов (рис. 2).
Врач должен иметь определенный опыт для проведения визуальной дифференциальной диагностики, в случаях размытых переходов на пограничных графиках между асимметричными и амодальными типами АРО, или, что встречается реже, между АРО полимодального и асимметричного типа.
1 2 3 4 5
Рис. 1. Примеры АРО больных ФП: 1 – мономодальный симметричный класс; 2 – мономодальный асимметричный класс; 3 – мономодальный инвертированный класс; 4 – полимодальный класс; 5 – амодальный класс
Рис. 2. Примеры атипичных АРО больных ФП
Поиск атипичных АРО при ФП был осуществлен в результате решения задачи автоматической категоризации данных. В этом случае ИНС на основе самоорганизации разбивает всю имеющуюся совокупность данных на несколько кластеров с образцами, сходными по внутренним параметрам.
По паттерну из 500 интервалов R-R строится АРО, представляющее собой черно-белое изображение размером 150150 пикселей [8, 10]. Если на изображении точка черная, то входной элемент сети кодируется значением 1. В противном случае – значением 0. Таким образом, вход сети X представляет собой вектор размера m1, где m – количество точек на АРО.
Каждый из n = 4 нейронов выходного слоя Y отвечает за свой кластер схожих образцов. В эксперименте участвовали только АРО трех мономодальных и одного полимодального классов. После обучения весовые коэффициенты нейронов являются координатами центров групп схожих примеров из обучающей выборки и образуют матрицу W размера nm.
Каждый из нейронов сети описывается двумя векторами. Один из векторов состоит из весовых коэффициентов связи с координатами входного вектора и имеет такую же размерность, как и входной вектор. Другой вектор состоит из координат самого нейрона на двумерной карте. Структурная схема самоорганизующейся ИНС приведена на рис. 3.
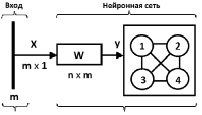
Рис. 3. Структурная схема самоорганизующейся ИНС для автоматической кластеризации АРО мономодальных и полимодального классов
Перед использованием сети в режиме кластеризации систему следует обучить [9].
Алгоритм обучения самоорганизующейся ИНС
Обучение ИНС включает следую- щие этапы:
1. Весовым коэффициентам {wkj},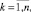 
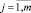всех нейронов сети присваиваются нулевые значения. Определяется 0 – начальный темп обучения. В нашем исследовании 0 = 0,3.
2. Выполняется случайный выбор входного вектора X из обучающего множества образцов.
3. Вычисляются квадраты расстояний между вектором X и нейронами сети по формуле
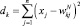, (1)
где N – дискретный момент времени.
4. Выбирается нейрон k*, который находится на наименьшем расстоянии от входного вектора X, выбранного на шаге 2.
5. Выполняется настройка весов нейрона с номером k* по формуле
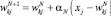. (2)
6. Значение скорости N уменьшается с течением времени обучения. В нашем исследовании значение параметра N уменьшалось в 2 раза через каждые 100 обучающих итераций.
7. Шаги 2–6 повторяются до тех пор, пока не будет выполнено максимально допустимое количество итераций. В нашем исследовании остановка алгоритма обучения происходила после каждой 1000 обучающих сеансов.
После ряда обучающих сессий нейроны сети оказываются в центрах близко расположенных друг к другу образцов из обучающей выборки. Поэтому весовые коэффициенты нейронов служат индикаторами встроенных статистических признаков, содержащихся во входных примерах. При этом сами нейроны становятся детекторами признаков различных классов входных образов.
Автоматическую кластеризацию входных примеров выполняет обученная ИНС. Для каждого входного вектора вычисляются расстояния до всех нейронов сети. Экземпляр АРО попадает в группу того нейрона, расстояние до которого оказалось наименьшим.
Результаты исследования и их обсуждение
В экспериментальной части работы было проанализировано 80 АРО больных ФП, сгруппированных экспертом по 20 примеров для каждого класса. Информация о выполненной экспертом классификации использовалась только для интерпретации результатов автоматической кластеризации и никак не учитывалась при обучении сети.
Компьютерная реализация разработанных моделей и алгоритмов была проведена в свободно распространяемой среде программирования Lazarus. В приложении запрограммированы: инициализация сети, обучение сети, функционирование обученной сети в режиме автоматической кластеризации АРО, а также построение карт самоорганизации.
Апробация показала, что сеть оказывается чувствительной к выбору стартовых координат нейронов, начальному темпу обучения и скорости его изменения. Численность и состав кластеров могут варьироваться при повторных сеансах обучения сети в результате использования случайного порядка выбора входных векторов.
Сеть автоматически выделяет в описанном банке авторегрессионных облаков четыре кластера, в каждом из которых по численности преобладают разновидности АРО мономодального симметричного, разновидности АРО мономодального асимметричного, разновидности АРО мономодального инвертированного и разновидности АРО полимодального классов соответственно. При этом в кластеры могут попадать образцы, которые эксперт интерпретировал как неклассический представитель АРО соответствующего типа. Это возможно и есть нетипичные структуры АРО, обладающие признаками нескольких классов. Примеры таких образцов приведены на рис. 4.
1 2 3 4 5
Рис. 4. Примеры атипичных АРО, выделенных сетью при автоматической кластеризации: 1 – АРО симметричного класса, определенное сетью в группу асимметричных АРО; 2 – АРО асимметричного класса, определенное сетью в группу симметричных АРО; 3 – АРО полимодального класса, определенное сетью в группу асимметричных АРО; 4 – АРО полимодального класса, определенное сетью в группу асимметричных АРО; 5 – АРО полимодального класса, определенное сетью в группу асимметричных АРО
С течением времени обучения происходит «дрейф» образцов из одного кластера в другой, что способствует уточнению численности и состава групп. При этом отмечается возврат некоторых примеров в «свои» группы и появление «чистых» групп без посторонних примеров.
Таким образом, в результате автоматической кластеризации множество АРО разбивается на четыре группы схожих примеров, что совпадает с мнением эксперта, проводившего классификацию. АРО, отнесенные ИНС при кластеризации к другим группам, являются пограничными случаями и внутренне тяготеют к нескольким классам, что служит основанием для их внимательного изучения и возможного уточнения результатов классификации.
Выводы
1. Сформирован банк данных из 80 АРО больных ФП, сгруппированных экспертом по 20 примеров для каждого класса. АРО построены по паттернам из 500 межпульсовых интервалов, полученных от пациентов в режиме on-line с помощью датчика пульса.
2. Разработана модель ИНС для решения задачи категоризации АРО больных ФП. ИНС имеет 22500 входов, через которые двоичные сигналы передаются на 4 нейрона, каждый из которых описывается двумя векторами. Один из векторов состоит из весовых коэффициентов связи с входными сигналами. Другой вектор состоит из координат самого нейрона на двумерной карте. Сформирован эффективный алгоритм для обучения ИНС. Весовые коэффициенты нейронов, вычисленные в результате обучения, служат статистическими индикаторами центров кластеров схожих по внутренним параметрам входным примерам.
3. Выполнена апробация разработанных моделей и алгоритмов в виде компьютерного приложения в свободно распространяемой среде программирования Lazarus. Отличительной особенностью приложения является наличие режимов автоматической кластеризации авторегрессионных графиков, построения карт самоорганизации и поиска атипичных примеров.
4. Проанализированы результаты решения задачи автоматической категоризации авторегрессионных облаков, относящихся к мономодальному и полимодальному классам. Независимая автоматическая категоризация авторегрессионных облаков соответствует кластерам АРО, установленных экспертом. Найденные нетипичные случаи АРО относятся к пограничным ситуациям и тяготеют к нескольким классам дифференциальной диагностики. Описанная в работе методика автоматического поиска атипичных случаев может быть перенесена на другие задачи медицинской диагностики.
Библиографическая ссылка
Хливненко Л.В., Пятакович Ф.А. ПОИСК АТИПИЧНЫХ ТИПОВ АВТОРЕГРЕССИОННЫХ ОБЛАКОВ МЕЖПУЛЬСОВЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ САМООРГАНИЗУЮЩЕЙСЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ // Современные наукоемкие технологии. – 2016. – № 5-2. – С. 296-300;URL: https://top-technologies.ru/ru/article/view?id=35902 (дата обращения: 18.04.2024).