Линтерование является завершающей стадией технологического процесса первичной обработки хлопка. Выходной продукцией его являются, прежде всего, технические и посевные семена, к которым предъявляются соответствующие требования, прежде всего со стороны опушенности. Предпринимались неоднократные попытки автоматизации этого процесса, но все они упирались в неразрешенную до сих пор задачу определения степени опушенности хлопковых семян как выходной величины. В настоящее время предложен алгоритм [3], позволяющий компенсировать ошибки, возникающие при контроле опушенности и использовании этого сигнала в качестве сигнала обратной связи. Такая система имеет ряд особенностей, которые требуют ее всестороннего исследования, в том числе и исследования на управляемость и наблюдаемость.
Экспериментальная часть
При исследовании САУ процесса линтерования с целью подготовки технических семян хлопчатника было выявлено, что задание можно осуществлять по двум входам. Первый вход – это задание с помощью образцовой пробы и второй – при образцовой пробе с произвольной опушенностью – по заранее заданному отношению в вычислительном устройстве. Таким образом, возникает вопрос, будет ли полученная система управляема и наблюдаема.
В такой системе и остается время чистого запаздывания, но его возникновение объясняется совершенно иными причинами. При отсутствии автоматического непрерывного контроля состояния процесса производится только арбитражный контроль, время которого весьма большое (не менее одного часа) и приводит к тому, что можно судить только о том объеме линтерованных хлопковых семян, которые уже миновали зону отделения линта от семени. Оно появляется из-за доставки семян от выхода из линтера до окна контрольной камеры элемента обратной связи транспортером [5] и значительно меньше по сравнению со временем, затрачиваемым на арбитражный анализ в автоматизированной системе. То есть блок-схема системы будет иметь вид, представленный на рис. 1.
Здесь объектом управления являются все блоки САУ, включая линтер, кроме регулятора. Сам датчик показан на рис. 2. Время чистого запаздывания определяется удаленностью камеры датчика от выхода линтера и скоростью движения транспортера [5].
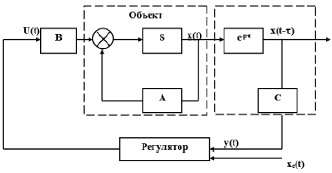
Рис. 1. Блок-схема САУ с местом возникновения чистого запаздывания: А, В, С – матрицы, описывающие систему в стандартной форме
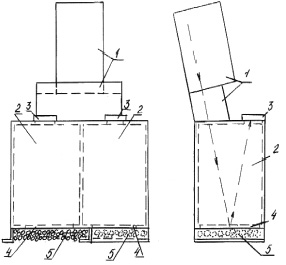
Рис. 2. Расположение оптической системы на камерах и отражение светового потока в них: 1 – оптическая система; 2 – камеры; 3 – фотоэлементы; 4 – окна в камерах; 5 – семена
Для составления матриц, описывающих блок-схему, представленную на рис. 1, запишем эквивалентную передаточную функцию замкнутой САУ:
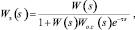
где W(s) – передаточная функция прямой цепи; Wо.с(s)e–τs – передаточная функция обратной связи.
Исполнительный элемент, в данном случае двигатель гребенки, имеет передаточную функцию апериодического звена I порядка с интегрированием, то есть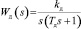 
? сам линтер согласно исследованиям, проведенным совместно с Ташкентским институтом ирригации и механизации представляет с достаточной точностью может быть описан как апериодическое звено первого порядка. То есть
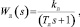
где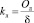 
– передаточный коэффициент линтера по каналу; Ол ? опушенность семян на выходе линтера в %; δ – зазор между гребенкой и колосниковой решеткой в мм; Tл – постоянная времени линтера, полученная экспериментальным путем.
Значения постоянных времени фотоэлементов как минимум на два порядка меньше меньшей постоянной времени Tд. Поэтому в случае, когда делителем в датчике является сигнал от образцовой пробы, ими можно пренебречь.
Для того чтобы избавиться от времени чистого запаздывания, воспользуемся известным способом замены этого звена апериодическим звеном второго порядка [1, 2] с постоянными времени Т1 и Т2 (рис. 3). При сделанных допущениях структурная блок-схема примет вид, показанный на рис. 4.
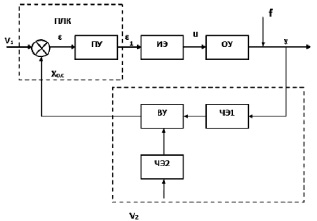
Рис. 3. Функциональная блок-схема САУ процесса линтерования
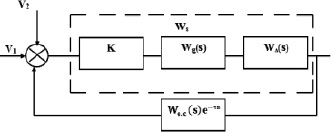
Рис. 4. Cтруктурная блок-схема САУ процесса линтерования
Учитывая введенные выше обозначения передаточных функций и их соответствие функциональным блокам, запишем передаточную функцию замкнутой САУ по входу V1:
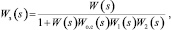(1)
где 
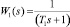и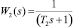 
– передаточные функции аппроксимирующие звено чистого запаздывания.
Поскольку значение входа V2 с преобразованием в вычислительном устройстве ВУ может быть сделанным равным V1, то передаточная функция системы по каналу V2 – y, будет записана так же, как формула (1).
Тогда уравнение согласно рис. 2 можно записать как
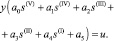(2)
Или в матричной форме:
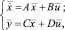(3)
где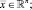 
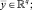
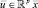– вектор состояния; 
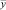– вектор выхода; 
– вектор управления; A – матрица системы; B – матрица управления; C – матрица выхода; D – матрица прямой связи. Введя обозначения [4],
y(t) = x1(t);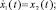 
,
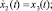
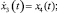
выразим из уравнения (2)
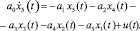
Поделив обе части полученного выражения на a0, запишем матрицы А и В. В случае одного воздействия они примут вид
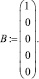
Если для управления используются два канала, матрица А остается без изменения, а матрица В примет вид В1:
Матрица управления Ру составляется из матриц-столбцов, полученных в результате действий над А и В по принципу, понятному из выражения
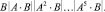(4)
Для случая одного воздействия после подстановки численных значений параметров для блоков САУ она запишется как Ру1, имеющая вид
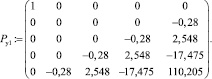
Ранг полученной матрицы Ру1 равен R = 5, т.е. условие управляемости выполнено.
При двух входных воздействиях матрица управляемости примет вид
И после операций, проведенных для численных значений, как в предыдущем случае, Ру2 также имеет ранг R = 5, т.е. система и в этом случае управляема.
Для практических целей в рассматриваемой САУ необходимо знать, наблюдаема ли система, поскольку только по выходному параметру можно определить начальное состояние системы, а это значит, что, исключив влияние неравномерности подачи семян, будет получена информация об опушенности семян после стадии джинирования.
Для этого составим матрицу наблюдаемости:
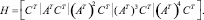
Поскольку все корни характеристического уравнения системы являются действительными, то транспонированные матрицы АТ и СТ будут являться сопряженными А* и С* . То есть
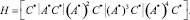
Для этого были найдены матрицы AT и CT и получена матрица наблюдаемости в среде MathCad. Аналогично случаю определения управляемости матрицы наблюдаемости для одного и двух управляющих воздействий будут иметь одинаковый вид:
Ранг матрицы Н, определенный также с помощью среды MathCad, будет равен 5. Иными словами, предлагаемая САУ будет являться и управляемой, и наблюдаемой при использовании управления системы как по одному каналу задания, так и при использовании двух каналов.
Выводы
Таким образом, при автоматизации стадии линтерования в технологическом процессе первичной обработки хлопка САУ, позволяющая исключать ошибки, возникающие от влияния факторов, неподлежащих контролю, является управляемой и наблюдаемой при использовании для задания как одного из двух возможных входов, так и обоих входов одновременно.
Библиографическая ссылка
Хуайер Абдулла Фарадж, Газиева Р.Т., Маслова Е.Е., Гривенко А.В., Байдюк А.П., Безуглов Д.В. ИССЛЕДОВАНИЕ САУ ЛИНТЕРОВАНИЯ ХЛОПКОВЫХ СЕМЯН НА УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ // Современные наукоемкие технологии. – 2016. – № 5-1. – С. 76-80;URL: https://top-technologies.ru/ru/article/view?id=35859 (дата обращения: 21.11.2024).