В «Концепции развития математического образования в РФ» (Распоряжение Правительства РФ от 24 декабря 2013 г.), в которой выделены проблемные группы мотивационного, содержательного и кадрового характера, одной из основных задач современного развития математического образования считается модернизация содержания учебных программ математического образования с учетом потребностей общества в специалистах различного профиля и уровня математической подготовки. Приоритетным направлением образовательной деятельности становится разработка методологических основ теории и практики обучения математике, а также выбора различных подходов и технологий обновления содержания математического образования на всех уровнях образовательного процесса. Обновление содержания образования должно способствовать формированию общекультурных и профессиональных компетенций, заявленных в ФГОС ВПО.
Следуя [4], под математическим образованием будем понимать учебно-воспитательный процесс обучения математике на всех ступенях непрерывного образования, при котором происходит не только усвоение определенной совокупности математических знаний, умений и навыков, но и развитие мышления обучаемых, формирование их нравственной и духовной культуры, а также соответствующих компетенций.
Математическое образование на профессиональном уровне назовем профессиональным математическим образованием. В профессиональном математическом образовании одним из ключевых действий становится формирование математической компетентности. Под математической компетентностью субъекта деятельности понимается «не только наличный, результативный уровень его подготовленности по математике, но и владение психолого-педагогическими знаниями и умениями» [5]. Математическая компетентность определяется не только математическими знаниями и умениями, но и ценностными ориентациями в социуме. А также мотивами деятельности, его общей культурой и способностью к развитию творческого потенциала, способностью понимать и воздействовать на духовный мир своих воспитанников, уважение к ним, восприятие обучаемого как личности. Кроме того, математическая компетенция рассматривается, с одной стороны, как способность структурировать данные, вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты, а с другой – как свойство личности, характеризующее его глубокую осведомленность в предметной области знаний, способного достигать значимых результатов и качества в математической деятельности. Тогда математическая компетенция и коммуникативная компетенция определяют общекультурные компетенции, а информационная – общепрофессиональные компетенции.
Таким образом, структурировать содержание математического образования следует с точки зрения постнеклассического типа рациональности, свойственного современному развитию науки, образования и общества, учитывающего соотнесенность знаний об объекте не только со средствами, но и с ценностно-целевыми структурами деятельности. В основу такого типа рациональности положена нелинейная (синергетическая) картина самоорганизующего мира, и при этом культурологический подход к образованию подразумевает, наряду с интеграцией знаний в единую картину мира, создание условий для духовно-нравственного становления личности на основе традиций мировой и национальных духовных культур.
Являясь частью целостной системы образования, содержание математического образования должно отвечать определенным социальным и организационным мотивам, представляемым содержанием образования по ФГОС ВПО. Содержание образования может быть представлено личностным, деятельностным, предметным и метапредметным содержанием. Под метапредметным содержанием понимается освоение универсальных учебных действий, а также универсальных способов мышления и действия, не являющихся специфическим для предметного материала. Такие способы базируются, например, на освоении категорий (как математических, так и философских), законов логики, природы и языков как универсальных форм представления знаний.
Следовательно, образование становится научной категорией, а структурирование содержания математического образования – предметом методологии математики, занимающейся конструированием закономерных связей компонентов методической системы с компонентами внешней среды и поиском методов исследования. Это означает, что необходимо формировать культуросообразное содержание математического образования и воссоздавать в образовательных структурах культурные образцы и нормы жизни через интеграцию образования в культуру. В таком контексте основным принципом образовательной деятельности становится принцип креативности. Кроме того, в содержании математического образования очень важно уметь выявить основные признаки фундаментальных понятий. Такие, например, как системность, представляющая собой соединение и взаимосвязь научных знаний в области математики, интеллектуальных и практических знаний и навыков творческой, поисковой деятельности, а также действенность и процессуальность, обладающие социально-педагогическим характером.
В формировании математических знаний почти на всех уровнях образования важную роль играют факторы как объективного, так и субъективного характера. Первые факторы, как обычно, связаны с знаково-символическими представлениями знаний, недостаточной разработанностью психолого-педагогических теорий обучения и воспитания, а вторые – чрезмерной интенсивностью и недостаточной структурированностью информационного потока знаний, слабой мотивационной и прикладной направленностью знаний, а также недостаточным методическим обеспечением учебной деятельности по части рефлексивной и творческой активности обучающихся. Поэтому математическое знание должно рассматриваться с более общих позиций, а именно с точки зрения психологии творчества и методологии математики. Математическая деятельность должна быть ориентирована преимущественно на изменение смыслового поля блендов, представляемого различными моделями структур математических объектов, и поиск адекватных им образов в физической реальности. Математическое моделирование в такой деятельности играет важную познавательную роль. Таким образом, нужны соответствующие педагогические технологии, в рамках которых содержание математического образования раскрывается наиболее эффективным образом. Проблемы структурирования содержания математического образования на различных уровнях образования рассматривались в работах Б.В. Гнеденко, А.Н. Колмогорова, Л.Д. Кудрявцева, Д. Пойа, А.Д. Александрова, А.Л. Вернера, С.Н. Дорофеева, В.И. Игошина, Ю.М. Колягина, В.А. Гусева, В.М. Монахова и др. Значительное количество фундаментальных работ отечественных и зарубежных авторов посвящено проблеме исследования содержания математического образования в средней и профессиональной школе (В.А. Далингер, А.Л. Жохов, А.Г. Мордкович, Е.И. Смирнов, В.И. Снегурова, Н.Х. Розов, В.А. Тестов и др.). Недостаточно изученными остаются вопросы содержания математического образования в процессе подготовки будущих учителей в вузе и выявления педагогических условий, способствующих профессиональной подготовке бакалавров педагогического образования в соответствии с требованиями ФГОС ВПО.
Цель настоящего исследования – на основе методологических принципов комплексного подхода к обучению математике выявить логические схемы, позволяющие оптимизировать процесс структурирования содержания математического образования в педагогическом вузе, способствующий формированию общекультурных и профессиональных компетенций.
Комплексный подход в стратегии дидактики математики высшей школы и новой образовательной парадигмы рассматривается как обобщение интегративного подхода, представляемого дуальной парой «процесс ? система» или «интеграция ? комплексификация». В такой паре первый компонент соответствует внешней форме деятельности, а второй – внутренней, и тем самым образование определяется и как процесс, и как система. Кроме того, мы считаем, что комплексный подход строится на основе закономерностей комплексного мышления, имеющего триадическую структуру, состоящую из компонентов математического, диалектического и жизнедеятельностного мышления. Каждый из компонентов комплексного мышления определяет соответствующую логику: математическое мышление – математическую логику, диалектическое мышление – диалектическую логику, жизнедеятельностное мышление – логику, релевантную жизни субъекта в обществе. Под комплексным подходом к профессиональному математическому образованию (или к профессиональной математической подготовке бакалавров педагогического образования) понимается совокупность приемов и способов воздействия на процесс обучения математике, а также профессиональную деятельность субъектов, двойственным образом объединяющая в единое целое процесс построения новых объектов (знаний) с полученным в результате такого действия сложным объектом (комплексом, системой), методами математического моделирования и синергетики. Основными принципами в методологии комплексного обучения математике (или в методологии «интегральной математики») являются: принципы единства противоположностей, соответствия и аналогии, определенности, симметрии, двойственности, инвариантности и математического моделирования [8]. С позиций эволюционной эпистемологии комплексный подход к обучению математике позволяет обнаруживать в развитии субъекта, содержания образования и среды обитания (общества) много общего, дающее системное восприятие окружающей действительности. Одним из общеметодологических принципов метапредметного содержания в методологии комплексного обучения математике будем считать принцип тринитарности как общесистемный структурный инвариант познавательной деятельности. Характерными особенностями комплексного подхода в методологии математики являются: выявление базисных понятий теории, отношений между ними; выделение структурных единиц и изучение общесистемных закономерностей в структурах различной природы по определенной логической схеме; исследование поведения структур и особенностей их перехода на другие уровни организации; использование законов диалектики и диалектической логики для анализа и построения математических моделей реальных объектов и явлений с точностью до изоморфизма; придание им духовно-ценностных значений.
Комплексный подход в структурировании математического образования мы рассматриваем с позиций культурологической соотнесенности образования к различным философским учениям (например, учение «о трех мирах» К. Поппера, учение Пирса о трех фундаментальных уровнях бытия и познания, выражаемых в категориях «первичности», «вторичности» и «третичности», учение о культурологических универсалиях В.С. Стёпина), а также технологических новаций в естественных науках (создание комплексонов в химии, построение полинуклеотидных цепей органических соединений в биологии, синтез новых элементарных частиц в физике и т.д.).
Таким образом, в комплексном подходе структурирования содержания математического образования синтезируются когнитивная, личностно-ориентированная и культурологическая парадигмы образования. В такой стратегии профессионального образования учебно-исследовательскую деятельность субъекта определим следующей структурной схемой: общество – культура – субъект – язык (знание, содержание образования) – объект (среда). Замечаем, что в такой профессиональной деятельности субъект становится связующим звеном трансдисциплинарного типа, рассматриваемого как новый тип связи между наукой, образованием и культурой, выполняющий социальный заказ общества. Социальный заказ общества определяется государственными стандартами различных уровней образования, в соответствии с которыми осуществляется профессионально-педагогическая подготовка бакалавров педагогического образования.
Анализ содержания математического образования проводится выявлением минимального числа количественных и качественных характеристик, свойственных множествам элементов и структурным составляющим компонентов, и определением стратегии синтеза новых математических объектов (понятий) с помощью структурных единиц по определенной логической схеме. Надо иметь в виду, что одним из основных тезисов методологии математики является следующее утверждение: иерархии любых сложных математических структур строятся с помощью различных комбинаций алгебраических (арифметических), топологических (геометрических) и порядковых (логических) структур [2]. Эти структуры связаны со структурами мышления, языков [6], физическими категориями (частицы, поля переносчиков взаимодействий, пространство-время), философско-религиозными началами (идеальное, материальное, религиозное), миропониманиями (реляционное, теоретико-полевое, геометрическое) [3, с. 514], моделями обучения (дискурсивно-аргументативная, эмотивно-суггестивная, исследовательская) [9, 10]. Такая связь фундаментальных структур различных предметных областей, определяемая общеметодологическим принципом тринитарности, позволяет построить более сложные структуры по одной и той же логической схеме. Эта схема может быть задана соответствующей математической моделью структуры. Такая модель синтезирует объективно-предметную и ценностно-смысловую стороны познавательной деятельности, подчиненной указанной выше структурной схеме деятельности и двойственной их отнесенности к объекту и субъекту познания. Двойственность выступает здесь внешней формой единства познавательных процессов: один становится фоном другого.
В такой стратегии структурирования содержания математического образования наряду с комплексным подходом актуальным становится и онтологический подход, который позволяет накапливать и структурировать информацию о процессе образования, дает целостную картину структуры и содержания образовательного процесса и обеспечения его качества, а также позволяет гибко реагировать на развитие и модификацию процесса. Онтологической структурной единицей в методологии познания (в математическом образовании, в частности) будем считать пару, определяемую двумя компонентами – мыслью и знаком. Обозначим ее l0 = (мысль, знак), или l0 = (t, s). Развитие этих понятий подчиняется следующему эволюционному ряду: мысль – смысл – мышление – размышление – разум; знак – значение – символ – признак – свойство – качество. Качество понимается как наличие существенных признаков, свойств, отличающих один предмет (или явление) от других, и оно, следовательно, соотносится с предметом, а разум – с упорядоченным действием, процессом, совершаемыим по определенным правилам.
Проанализируем комплексный подход к структурированию математического образования с позиций культурологического подхода на следующем примере. В качестве базисных понятий геометрии рассмотрим точки, прямые, плоскости, а базисных понятий арифметики – числа. Выберем на плоскости (в пространстве) три точки А, В, С, принадлежащие одной прямой. Эти точки на прямой порождают три направленных отрезка (вектора) АС, СВ, АВ. Равенством
АС = α СВ (*)
в геометрии определяется так называемое простое отношение трех точек А, В, С. Будем считать, что точки, направленные отрезки (векторы) и числа – это базовые единичные элементы, а равенство (*) – онтологическая структурная единица Проследим за проявлением этой структурной единицы в структурах различной природы. Введя операции сложения векторов и умножения вектора на число, подчиняя их определенным аксиомам, получим векторное пространство. Дополним его точками и аксиомами, связывающими точки с векторами и числами. Тогда если в таком пространстве преобразование таково, что оно любую прямую с заданными на ней тремя точками переводит в прямую с соответствующими образами этих точек и при этом для них сохраняется равенство (*), то такое преобразование называется аффинным. Множество всех аффинных преобразований плоскости (пространства) образует группу. Итак, в аффинной геометрии изучают все свойства фигур, инвариантные относительно аффинных преобразований (принцип инвариантности), и онтологическая структурная единица, определяемая равенством (*), становится одним из базовых понятий аффинной геометрии.
Дополняя аксиоматику аффинного пространства аксиомами скалярного произведения (принцип дополнения или двойственности), получим евклидово пространство. Так как в евклидовой геометрии изучаются свойства фигур, инвариантные относительно группы движений, а при движениях равенство (*) также сохраняется, то онтологическая структурная единица, определяемая этим равенством, является базовым понятием и евклидовой геометрии. Простое отношение трех точек прямой является базовым понятием и проективной геометрии. В самом деле, в проективной геометрии изучаются свойства фигур, инвариантные относительно группы проективных преобразований, а проективное преобразование, как известно, определяется как преобразование, сохраняющее сложное отношение четырех точек (АВ, СD), выражаемое двумя простыми отношениями трех точек (АВ, С) и (АВ, D).
Таким образом, понятие простого отношения трех точек прямой является одним из фундаментальных понятий геометрии.
Проанализируем различные культурологические феномены онтологической структурной единицы, определяемой равенством (*). Если в этом равенстве значение α заменить на 1,618, то получим известное «золотое сечение» как частный случай простого отношения [1]. Оно может быть выражено с помощью единицы и как бесконечное извлечение корня в виде
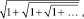
и как бесконечная цепная дробь в виде
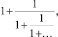
и как предельное значение отношения последующего элемента к предыдущему элементу в последовательности Фибоначчи и т.д.
Особое ценностное значение этого понятия следует выделить в образовательном процессе применительно к непосредственной жизнедеятельности. Так, например, оптимальные размеры сторон прямоугольника (листов бумаги, фотопластинок, фотопленок, размеры кино- и телеэкранов и т.д.) выражаются исходя из пропорции «золотого сечения». Или пропорции тел, спиральные структуры, параметры биоритмов и т.д. также обладают свойствами, характерными для золотого сечения. Кроме того, в биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Поэтому «золотое сечение» признано универсальным законом живых систем. Носители генетического кода – молекулы ДНК и РНК – имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.
В культурологическом аспекте «золотое сечение» проявляется, например, в музыке, поэзии, живописи и в архитектуре. Оказывается, некий скачок развития темы, сюжета, настроения происходит в точках золотого сечения. Проявление золотого сечения в виде «золотой середины» или «срединного пути» характерно также религиозно-философским и социально-экономическим учениям. Так, например, в конфуцианстве обычно выделяются 22 основные категории, среди которых категории «чжуньюн» (золотая середина), «датун» (великое единение, согласованность, полная гармония, тождество), «сяокан» (средний достаток) являются центральными структурообразующими категориями. Кроме того, почти все учение Буддизма связано с поиском срединного пути.
Проявление тринитарного отношения между базовыми понятиями различных теорий характерно и в более общем контексте. Так, если цивилизацию рассматривать как целостную систему, в которой взаимно переплетены, дополняя друг друга, материальное и духовное воспроизводство, экономика и политика, социальные отношения и культура, то качество цивилизации определяется оригинальным свойством каждого из трех указанных структурообразующих компонентов и их неповторимым единством (Ю.В. Яковец, Э.Д. Фролов). Кроме того, тринитарность как общесистемный принцип характерна и для мир-системного подхода (А. Тойнби, О. Шпенглер). Например, капиталистическая мир-система состоит из «ядра» (наиболее высокоразвитые страны), «полупериферии» (страны социализма в ХХ в.) и «периферии» (страны третьего мира). Понятие «способ производства» в мир-системе заменяется термином «способ накопления» (К. Чейз-Данн, Т. Холл). Способов накопления три:
1) основанный на родственных связях;
2) даннический;
3) рыночный.
В соответствии с этими способами выделяются три мир-системы: основанные на родстве, даннические (первичные государства, первичные империи, мир-системы с многими центрами), капиталистические.
Таким образом, культурологический взгляд на профессиональное математическое образование становится одним из ключевых факторов в структурировании содержания образования с позиций комплексного подхода к обучению математике. Такой подход к математическому образованию позволяет обнаруживать единство законов природы, математической деятельности и мышления с точки зрения системного восприятия математического знания и формирования общекультурных и профессиональных компетенций субъектов профессиональной образовательной среды. Общеметодологический принцип тринитарности способствует развитию у обучающихся категориального мышления, на основе которого строится логическая схема, связывающая фундаментальные понятия структур различных предметных областей. Такое единство действий создает целостную картину более сложных структур межпредметного содержания и всего содержания образовательного процесса в целом. Онтологические структурные единицы, выделяемые на математических моделях структур, и основополагающий принцип тринитарности, связывающий базовые понятия данной теории в единое целое, способствуют обобщению математических знаний для анализа различных религиозно-философских и социально-экономических учений. Таких, например, теорий, как математическая эвентология, которая является научной теорией о событийном в разуме и материи, строящейся на триаде понятий: событие, вероятность события, ценность события; аутентичная синергетика, которая рождается и развивается на пересечении, конструктивном синтезе трех начал: нелинейного моделирования, практической философии и предметного знания; фрактальный анализ; синергетическая геометрия и т.д.
Библиографическая ссылка
Ярахмедов Г.А., Магомедов Х.М. О КУЛЬТУРОЛОГИЧЕСКОМ АСПЕКТЕ СТРУКТУРИРОВАНИЯ СОДЕРЖАНИЯ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ В ПЕДАГОГИЧЕСКОМ ВУЗЕ // Современные наукоемкие технологии. 2016. № 4-2. С. 411-416;URL: https://top-technologies.ru/ru/article/view?id=35844 (дата обращения: 05.03.2026).



