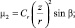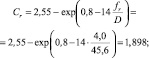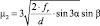Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чепур П.В. 1 Тарасенко А.А. 1 Юргевич А.В. 2

---

1 Тюменский государственный нефтегазовый университет

2 ООО НПП «Симплекс»

Авторами разработана конечно-элементная модель резервуара РВС-20000 со стационарной щитовой кровлей, состоящей из радиальных и кольцевых балок, а также листового настила в соответствии с типовым проектом ТП 704-1-60. В модели учитываются все нагрузки согласно действующим нормативным документам. Предложена расчетная схема, в которой учитывается неравномерное распределение снегового покрова согласно СП 20.13330.2011 для наиболее неблагоприятного варианта воздействия в сочетании с вакуумметрическим давлением. В работе получены эпюры распределения действующих напряжений и деформаций кровли РВС-20000, по которым установлено, что при действующих максимальных эксплуатационных нагрузках напряжения в металлоконструкциях резервуара не превышают допускаемые и конструкцией обеспечивается достаточный запас прочности. Также максимальные прогибы элементов кровли не превышают допускаемые значения, предписанные СП 20.13330.2011.

Статья в формате PDF

0 KB

МКЭ

ANSYS

НДС

прочность

напряжения

крыша

кровля

резервуар

настил

покрытие

1. Васильев Г.Г, Тарасенко А.А., Чепур П.В., Гуань Ю. Анализ сейсмостойкости вертикального стального резервуара РВСПК-50000 с использованием линейно-спектрального метода // Нефтяное хозяйство. – 2015. – № 10. – С. 120–123.

2. Тарасенко А.А., Чепур П.В. Эволюция взглядов на вопросы определения величины допустимых осадок резервуаров // Фундаментальные исследования. – 2014. – № 12–1. – С. 67–84.

3. Тарасенко А.А., Чепур П.В., Грученкова А.А. Использование критериев стандарта API-653 для оценки допустимой величины осадки днища резервуаров // Фундаментальные исследования. – 2014. – № 12–7. – С. 1418–1422.

4. Тарасенко А.А., Чепур П.В., Грученкова А.А., Соколов С.С. Оценка влияния трубопроводов системы подслойного пожаротушения на напряженное состояние резервуара при осадке основания // Фундаментальные исследования. – 2014 – № 11–8. – С. 1698–1702.

5. Тарасенко А.А., Чепур П.В., Тарасенко Д.А. Численное моделирование процесса деформирования резервуара при развитии неравномерных осадок // Нефтяное хозяйство. – 2015. – № 4. – С. 88–91.

6. Тарасенко А.А., Чепур П.В., Шарков А.Е., Гретченко Д.А. Технология диагностики вертикальных стальных резервуаров без снятия антикоррозионного покрытия // Фундаментальные исследования. – 2014. – № 9–8. – С. 1703–1708.

7. Чепур П.В. Напряженно-деформированное состояние резервуара при развитии неравномерных осадок его основания: дис. канд. техн. наук – М.: Российский государственный университет нефти и газа имени И.М. Губкина, 2015. – 181 с.

8. Чепур П.В., Тарасенко А.А., Грученкова А.А. Анализ возможности использования критериев стандарта API-653 для оценки неравномерной осадки резервуаров отечественных типоразмеров // Фундаментальные исследования. – 2014. – № 12–3. – С. 514–519.

9. Чепур П.В., Тарасенко А.А. Особенности совместной работы резервуара и устройств размыва донных отложений винтового типа // Фундаментальные исследования. – 2015. – № 2–8. – С. 1671–1675.

10. Чирков С.В., Тарасенко А.А., Чепур П.В. Определение оптимального количества тросов поддержки днища при подъеме резервуара // Известия вузов. Нефть и газ. – 2014. – № 5. – С. 72–78.

Вертикальные стальные резервуары (РВС) – высокоответственные сооружения, безотказность работы которых определяет стабильность системы магистрального транспорта нефти. Одним из наиболее нагруженных элементов резервуара является его кровля. На крышу РВС действуют сложные сочетания нагрузок, которые включают в себя: постоянную (собственный вес), длительную (избыточное давление, вакуум и вес снегового мешка) и кратковременную (воздействие ветрового потока) нагрузки. Стационарное покрытие резервуара состоит из балочного каркаса из радиальных и кольцевых балок, а также листового настила. Конструкция, состоящая из системы балок и листового настила, опирается на верхнее кольцо жесткости, через которое суммарная нагрузка передается на стенку резервуара. В актуализированных нормативных документах ужесточились требования в части обеспечения прочности конструкций кровли при воздействии неравномерно распределенного снегового покрова, т.е. снеговых мешков. В данной статье авторами предлагается проанализировать предельные прочностные характеристики металлоконструкций сферической кровли при действующих максимальных эксплуатационных нагрузках для наиболее распространенного в РФ типоразмера резервуара – РВС-20000.

Согласно ГОСТ 31385-2008 при расчете стационарных крыш учитывают первое основное сочетание нагрузок, в котором участвуют максимальные значения расчетных нагрузок, действующих на крышу от:

– собственного веса крыши с оборудованием и площадками;

– веса снега при равномерном и неравномерном расположении (значение определяется в соответствии с картой климатического районирования по снеговым районам);

– вакуума в газовоздушном пространстве Pвак = 250 Па.

Стационарная крыша должна выдерживать действие аварийного избыточного давления, равного 1,6·Pизб = 3200 Па.

Геометрические параметры и конструктивная схема щита стационарной кровли представлены в табл. 1 и на рис. 1.

Таблица 1

Геометрические параметры крыши

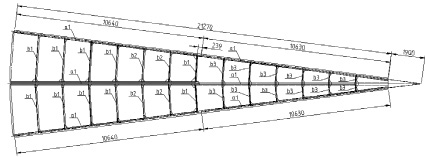
Рис. 1. Геометрическая схема щита кровли РВС-20000

При учете снеговой нагрузки были рассмотрены три варианта и получены результаты расчета НДС металлоконструкций кровли для наиболее неблагоприятного случая – неравномерно распределенной снеговой нагрузки.

– снеговая нагрузка – вариант 1 (снег, равномерно распределенный) по схеме Г.13 СП 20.13330.2011 μ1 = 1,0;

– снеговая нагрузка – вариант 2 (снег, неравномерно распределенный) по схеме Г.13 СП 20.13330.2011. Коэффициент перехода от веса снегового покрытия земли к снеговому покрытию на кровле μ2 по табл. 2 (и схеме на рис. 2);

– снеговая нагрузка – вариант 3 (снег, неравномерно распределенный) по схеме Г.13 СП 20.13330.2011. Коэффициент перехода от веса снегового покрытия земли к снеговому покрытию на кровле μ2 по табл. 2 (и схеме на рис. 2).

Таблица 2

Схема распределения снега на сферической крыше. Определение коэффициента распределения снеговой нагрузки μi

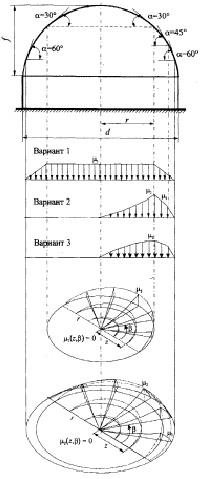
Рис. 2. Схема распределения снега на сферической крыше

С учетом условия обеспечения прочности конструкций сферической крыши в виде отсутствия превышения предела текучести используемого типа стали 09Г2С модель поведения материала принималась по линейному закону

σ = E?ε, (1)

где σ – напряжения, возникающие в материале, МПа; E = 2,1·105 МПа – модуль Юнга.

Эквивалентные напряжения по Мизесу σeqv, МПа, в металлоконструкциях сферической крыши не должны превышать предела текучести стали с учетом коэффициентов запаса согласно требованиям РД-23.020.00-КТН-018-14.

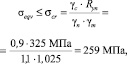(2)

где Ryn = 325 МПа – предел текучести стали 09Г2С в соответствии с СП 16.13330.2011; γc = 0,9 – коэффициент условий работы сферической крыши; γn = 1,15 – коэффициент запаса по назначению резервуара РВС-20000; γm = 1,025 – коэффициент запаса по материалу (для стали 09Г2С согласно СП 16.13330.2011).

Эквивалентные напряжения по Мизесу σeqv рассчитываются по формуле

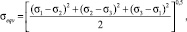(3)

где σ1, σ2, σ3 – главные напряжения в конечно-элементной модели, МПа.

Устойчивость несущего каркаса проверяется по результатам расчета модели в нелинейной геометрической постановке. Предельные деформации сферической крыши Δz, мм, не должны превышать принимаемые в соответствии с требованиями СП 20.13330.2011 значения:

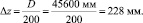(4)

Компьютерное моделирование и расчет конструкций сферической крыши производится с использованием программного комплекса, реализующего метод конечных элементов, ANSYS 16.1.

Компьютерная модель крыши представляет собой систему металлоконструкций, включающую радиальные несущие балки, опорное кольцо, листовой настил и узел сопряжения опорного кольца со стенкой. Для создание реальных условий работы опорного кольца в модель включена стенка высотой 12 м. Радиальные элементы, элементы опорного кольца и участка стенки соединены между собой жестко.

Граничные условия – нижняя кромка стенки жестко защемлена от перемещений и поворотов по всему периметру.

При компьютерном моделировании были применены следующие типы встроенных элементов ANSYS 16.1:

– для создания конечных элементов площадей – Shell181, реализующий механические свойства сжатия, растяжения и мембранные свойства путем привязки к существующей геометрии моделируемого объекта и задания толщины элемента;

– для создания конечных элементов балок несущего каркаса – Beam188, реализующий механические свойства сжатия, растяжения и изгиба путем привязки к существующей геометрии моделируемого объекта и задания сечения элемента;

– для создания снеговой нагрузки, действующей в соответствии с требованиями СП 20.13330.2011 – Surf154, реализующий приложение нагрузок и воздействий с привязкой к системе координат компьютерной модели;

– при генерации конечно-элементной сетки выполнялось разбиение модели на четырехузловые прямоугольные элементы размерами 0,5×0,5 м со сгущением стороны линейного объекта в контактных зонах до 0,01 м.

Геометрия, расположение узловых точек и направления прикладываемых нагрузок и воздействий конечных элементов Shell181, Beam188 представлены на рис. 3.

Расчетная схема РВС-20000 с разбиением КЭ-модели на сетку представлена на рис. 4, где показаны все действующие нагрузки на сооружение, а также граничные условия. Также на рис. 4 отражена конструкция радиальных и кольцевых балок кровли. Разработанная модель реализует фактическое состояние крыши при сборке секторов, изготовленных в заводских условиях с приваркой настила двусторонним сварным соединением.

Согласно пункту 8.4.4.а СП 16.13330.2011 устойчивость балок кровли следует считать обеспеченной при передаче нагрузки на балку через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и связанный с ним с помощью сварки. Следовательно, проверке на устойчивость подлежат только кольцевые балки секторов заполнения. Максимальные усилия, действующие в кольцевых элементах каркаса, приведены в табл. 3 для наиболее неблагоприятного сочетания нагрузок.

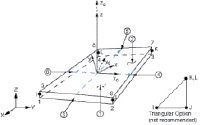
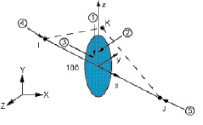
Рис. 3. Геометрия, расположение узловых точек (I, J, K, L) и направления прикладываемых нагрузок и воздействий (указаны цифрами) КЭ

Таблица 3

Максимальные усилия, действующие в элементах каркаса кровли

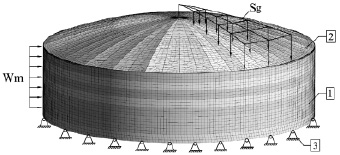
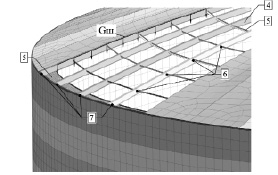
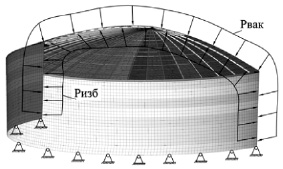
Рис. 4. Расчетная схема: 1 – стенка; 2 – листовой настил кровли; 3 – жесткая заделка; 4 – радиальная несущая балка кровли; 5 – кольцевая балка (уголок); 6 – жесткое соединение радиальной и кольцевых балок; 7 – жесткое соединение радиальных несущих балок с опорным кольцом; Wm – ветровая нагрузка; Sg – снеговая нагрузка для наиболее невыгодного случая распределения снегового покрова; Gш – нагрузка от собственного веса настила, балок и оборудования на кровле; Pизб – нагрузка от избыточного давления паров нефти; Pвак – вакуумметрическое давление

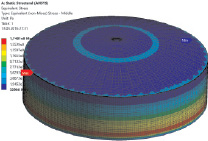
По результатам расчета элементов каркаса сферической крыши при действии нагрузок для наиболее неблагоприятного варианта установлено, что максимальные эквивалентные напряжения по Мизесу σeqv, МПа, в данных элементах не превышают предельных значений согласно критерию (2). Эпюра распределения эквивалентных напряжений представлена на рис. 5, а.

а б

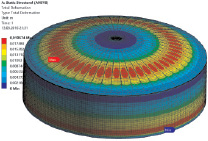
Рис. 5. Эпюры распределения действующих эквивалентных напряжений (а) и деформаций (б) в металлоконструкциях РВС-20000

Анализируя деформации стационарной кровли (рис. 5, б) при действующих нагрузках, установлено, что они не превышают допустимое согласно СП 20.13330.2011 значение – 228 мм. Максимальные деформации элементов кровли составили ?Z = 19,6 мм.

Выводы

1. Авторами разработана конечно-элементная модель резервуара РВС-20000 со стационарной щитовой самонесущей кровлей, состоящей из радиальных и кольцевых балок, а также листового настила. В модели учитываются все эксплуатационные нагрузки согласно требованиям действующих нормативных документов СП 20.13330.2011, ГОСТ 31385-2008.

2. Предложена расчетная схема, в которой учитывается неравномерное распределение снегового покрова согласно СП 20.13330.2011 для наиболее неблагоприятного варианта воздействия в сочетании с вакуумметрическим давлением.

3. В работе получены эпюры распределения действующих напряжений и деформаций кровли РВС-20000, по которым установлено, что при действующих максимальных эксплуатационных нагрузках напряжения в металлоконструкциях резервуара не превышают допускаемые (σeqv < [σ], 174 < 259 МПа) и конструкцией обеспечивается запас прочности – 1,5. Также максимальные прогибы элементов кровли (19,67 мм) не превышают допускаемые значения, предписанные СП 20.13330.2011.

Библиографическая ссылка