Технологический процесс фторирования урана требует точного дозирования оксида урана, надёжности и безопасности электропривода шнека загрузки.
В настоящее время в качестве электропривода (ЭП) шнека загрузки, служащего для подачи в пламенный реактор оксида урана в виде мелкокристаллического вещества при фторировании урана, используется ЭП постоянного тока, недостатками которого является низкая надёжность машины постоянного тока из-за наличия щёточно-коллекторного узла, сложность в обслуживании, высокая стоимость эксплуатации и массогабаритные показатели [4]. Использование ЭП на базе асинхронного двигателя с короткозамкнутым ротором (АД) и реализация современных методов управления им даёт высокие показатели эффективности и работоспособности таких электроприводов [5]. Широкое использование АД в массовом и специализированном электроприводе можно объяснить его высокой надежностью, обусловленной отсутствием щеточно-коллекторного узла и постоянных магнитов, простотой конструкции, малыми габаритами и моментом инерции ротора, отсутствием коммутационных ограничений по скорости и току и т.д. [1].
Поэтому разработка, исследование и внедрение современного частотно-регулируемого асинхронного ЭП для шнека загрузки пламенного реактора является актуальной и соответствует требованиям времени.
Оптимизация контуров регулирования системы частотно-управляемого асинхронного электропривода
Характерной особенностью частотно-регулируемых ЭП переменного тока является относительно большая инерционность в цепи обратной связи контуров регулирования тока, потокосцепления и скорости [3]. Поэтому для их оптимизации не может быть применена классическая теория оптимизации систем подчиненного регулирования с безынерционной обратной связью. Для оптимизации контуров регулирования с инерционной обратной связью используем методы, изложенные в [2]. Упрощенная структурная схема системы частотно-управляемого асинхронного ЭП приведена на рис. 1.
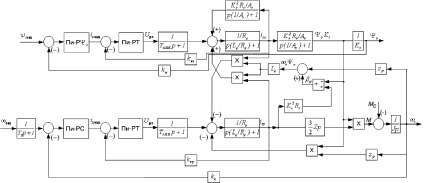
Рис. 1. Упрощенная структурная схема системы частотно-векторного управления асинхронным двигателем
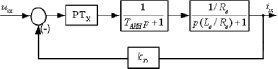
Рис. 2. Структурная схема контура для управления составляющей тока статора isx
Из структурной схемы видно, что в системе имеются контуры регулирования составляющей тока статора по оси х (с регулятором РТх), составляющей тока статора по оси у (с регулятором РТу), контур регулирования скорости двигателя (с регулятором РС) и контур регулирования, определяющий магнитный поток обмотки ротора машины (с регулятором РYr).
Оптимизация контура тока
Оптимизацию контура тока осуществляем без учёта перекрёстных связей двигателя и при нулевых заданиях на скорость и поток. Структурная схема контура приведена на рис. 2.
С учётом параметров контура выбираем пропорционально-интегральный (ПИ) – регулятор с передаточной функцией
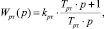
где Tpm = Te = Treg – постоянная времени регулятора; 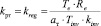 – коэффициент усиления регулятора; kinv – коэффициент обратной связи по току; am – коэффициент оптимизации контура тока по модульному оптимуму (МО).
– коэффициент усиления регулятора; kinv – коэффициент обратной связи по току; am – коэффициент оптимизации контура тока по модульному оптимуму (МО).
Передаточная функция разомкнутого контура тока
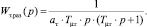 (1)
(1)
Передаточная функция замкнутого контура тока
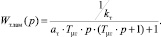 (2)
(2)
При моделировании в качестве АД используется двигатель D09SA4 со следующими каталожными данными: синхронная скорость вращения n0 = 1500 об/мин, номинальное фазное напряжение U = 220 В, номинальная мощность двигателя Pн = 1,1 кВт, номинальное скольжение S = 0,067, коэффициент полезного действия в режиме номинальной мощности ηн = 76,3 %, коэффициент мощности в режиме номинальной мощности cos φн = 0,78, кратность максимального момента 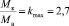 , кратность пускового момента
, кратность пускового момента 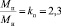 , кратность минимального момента
, кратность минимального момента 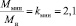 , кратность пускового тока
, кратность пускового тока 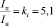 .
.
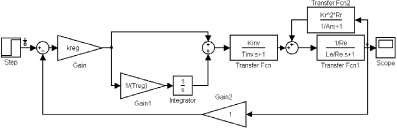
Рис. 3. Имитационная модель контура тока для управления составляющей тока статора isx
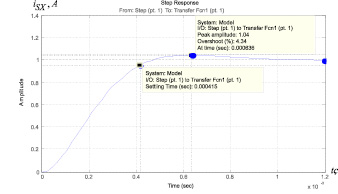
Рис. 4. Переходная характеристика i(t) контура тока
Таблица 1
Динамические показатели качества регулирования контура тока
|
Показатели |
Ожидаемые |
Полученные |
|
σ, % |
4,32 |
4,34 |
|
|
0,00041 |
0,000415 |
|
|
7100 |
7120 |
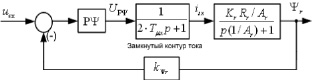
Рис. 5. Структурная схема контура потокосцепления
Результаты моделирования переходных процессов в контуре тока, настроенного на модульный оптимум при отработке ступенчатого входного воздействия UЗМ UЗМ = 1 о.е., представлены в виде переходной характеристики i(t) на рис. 4.
Показатели качества работы контура тока сведены в табл. 1.
Анализ полученных результатов моделирования показывает, что настройка контура тока с ПИ-регулятором близка к настройке на МО системы 2-го порядка. Контур является астатической системой 1-го порядка по управлению.
Оптимизация контура потокосцепления
Структурная схема контура потокосцепления приведена на рис. 5.
С учетом параметров контура выбираем ПИ-регулятор с передаточной функцией
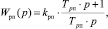 (3)
(3)
где kрп – коэффициент усиления; 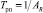 – постоянная времени регулятора.
– постоянная времени регулятора.
Полная передаточная функция разомкнутого контура потокосцепления
По структурной схеме контура потокосцепления (рис. 5) составим имитационную модель, которая приведена на рис. 6.
Результаты моделирования переходных процессов в контуре потокосцепления, настроенного на МО, при отработке ступенчатого входного воздействия Uзп.макс = 1 В приведены в виде переходной характеристики Yr(t) на рис. 7.
Показатели качества работы замкнутого контура потокосцепления приведены в табл. 2.
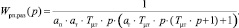 (4)
(4)
Полная передаточная функция замкнутого контура потокосцепления
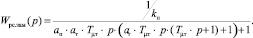 (5)
(5)
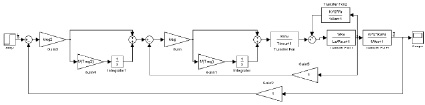
Рис. 6. Имитационная модель контура потокосцепления
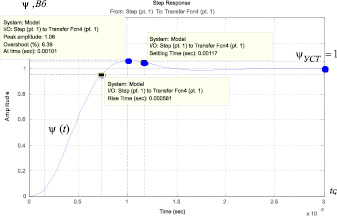
Рис. 7. Переходная характеристика контура потокосцепления
Таблица 2
Динамические показатели качества регулирования замкнутого контура потокосцепления
|
Показатели |
Ожидаемые |
Полученные |
|
σ |
8,14 |
6,39 |
|
|
0,0007 |
0,000581 |
|
|
0,0012 |
0,00117 |
|
|
5000 |
4640 |
|
|
3500 |
3440 |
Анализ полученных результатов моделирования контура потокосцепления показывает, что они практически совпадают с ожидаемыми качественными показателями работы контура тока. Небольшие расхождения в величинах качественных показателей контура потокосцепления и тока находятся в пределах допустимой погрешности.
Оптимизация контура скорости
Структурная схема контура скорости приведена на рис. 8.
С учётом параметров контура выбираем ПИ-регулятор с передаточной функцией
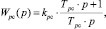 (6)
(6)
где kрс – коэффициент усиления; ac – коэффициент оптимизации контура скорости на СО; Tμc = aт?Tтп (о.е.) – малая постоянная времени контура; T2 = Tрс (о.е.) – большая постоянная времени контура.
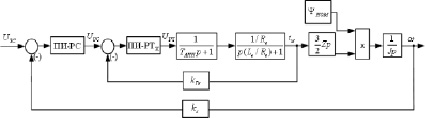
Рис. 8. Структурная схема контура скорости, настроенного на симметричный оптимум
Передаточная функция разомкнутого контура скорости, настроенного на СО:
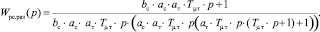
Передаточная функция замкнутого контура скорости без фильтра на входе:
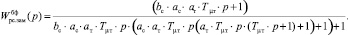
Передаточная функция замкнутого контура скорости с фильтром на входе:
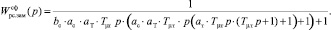
По структурной схеме контура скорости, настроенного на СО (рис. 8), построена имитационная модель, представленная на рис. 9.
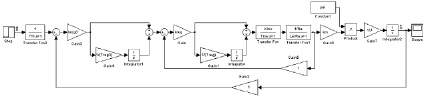
Рис. 9. Имитационная модель контура скорости, настроенного на СО
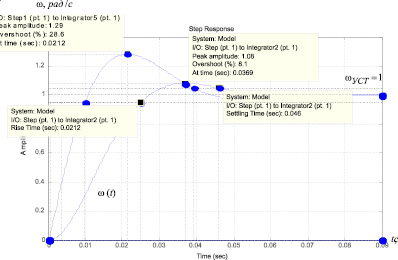
Рис. 10. Переходные характеристики υ(t) контура скорости, настроенного на СО
Таблица 3
Динамические показатели качества регулирования замкнутого контура скорости с фильтром на входе
|
Показатели |
Ожидаемые |
Полученные |
|
σ, % |
8,1 |
8,1 |
|
|
0,02176 |
0,0212 |
|
|
0,03248 |
0,046 |
|
|
141,24 |
124 |
|
|
101,69 |
103 |
Результаты моделирования переходных процессов в контуре скорости, настроенного на симметричный оптимум (c фильтром и без фильтра на входе), при отработке ступенчатого входного воздействия Uзс.макс = 1 В приведены в виде переходных характеристик υ(t) на рис. 10.
Динамические показатели качества регулирования замкнутого контура скорости с фильтром на входе приведены в табл. 3.
Выводы
1. Установлено, что применение частотно-регулируемого асинхронного электропривода для шнека загрузки пламенного реактора позволяет обеспечить динамические показатели качества регулирования, сравнимые с электроприводом постоянного на базе двигателя с независимым возбуждением.
2. Анализ динамических показателей качества регулирования основных контуров системы частотно-регулируемого асинхронного электропривода, полученных в результате моделирования и ожидаемых, показывает, что они практически не отличаются друг от друга. Небольшая погрешность между ними связана с введением упрощений в расчетах при оптимизации контуров. Следует отметить, что качество переходных процессов в контуре скорости с фильтром на входе несколько лучше, чем без него.
Библиографическая ссылка
Дементьев Ю.Н., Власов А.И., Кояин Н.В., Умурзакова А.Д. ОПТИМИЗАЦИЯ КОНТУРОВ ЧАСТОТНО-РЕГУЛИРУЕМОГО АСИНХРОННОГО ЭЛЕКТРОПРИВОДА ШНЕКА ЗАГРУЗКИ ПЛАМЕННОГО РЕАКТОРА // Современные наукоемкие технологии. 2016. № 4-2. С. 235-241;URL: https://top-technologies.ru/ru/article/view?id=35809 (дата обращения: 08.02.2026).




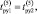 о.е.
о.е.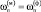 , o.e.
, o.e.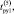 о.е.
о.е.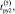 о.е.
о.е.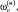 о.е.
о.е.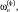 о.е.
о.е.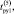 о.е.
о.е.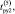 о.е.
о.е.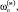 о.е.
о.е.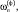 о.е.
о.е.