Сегодня ощущается большая потребность в личности, обладающей критическим мышлением: умеющей подвергнуть сомнению устоявшиеся мнения и суждения, способной вести диалог, определять суть проблемы и альтернативные пути ее решения, отличать факт, который всегда можно проверить, от предположения и личного мнения, и поэтому формирование такой личности стало одной из ведущих проблем российского образования.
Исследователями В.П. Зинченко [4], А.А. Тюковым [6], В.М. Розиным [5] и др. обоснован факт, что студент может получить полноценное знание только при условии развития критического мышления. Поэтому в современном высшем образовании необходимо перенесение акцента с информационного обучения на смыслопоисковое. Это требует изменений в подходах к процессу обучения, поиска наиболее эффективных путей формирования критического мышления студента, оценки причин и смыслов происходящего.
Кроме того, необходимость формирования критического мышления у студентов обусловлена следующими причинами:
1. В условиях неограниченного доступа к информации важно уметь ориентироваться в ее потоках, анализировать, различать главное и второстепенное, критически осмысливать информацию и т.д.
2. В связи с уменьшением в учебном процессе количества контактных часов преподавателя и студента по учебному плану при неизменном объеме учебного материала необходимо развивать познавательную самостоятельность, самообразовательную деятельность, учить студентов критически мыслить.
Причем в процессе формирования критического мышления обучающихся математические дисциплины являются наиболее эффективными. Математика как никакой другой предмет позволяет не просто решать сформулированную задачу, а делать это различными способами, применяя в том числе такие методы работы с информацией, как поиск, анализ, синтез, переработка и представление, учит аргументированности, доказательности и обоснованности рассуждений и т.д.
Под критическим мышлением мы понимаем процесс оценки достоверности, точности или ценности чего-либо, способность оценки искать и находить причины и альтернативные точки зрения, воспринимать ситуацию в целом и изменить свою позицию на основе фактов и аргументов [2]. Критическое мышление называют логическим или аналитическим мышлением. Кроме того, это мышление рефлексивное, оценочное, для которого знание является не конечной, а отправной точкой [1]. Оно основано на убедительной аргументации, что подразумевает владение обучающегося коммуникативными умениями.
Таким образом, развитие критического мышления студента способствует:
– развитию информационной культуры обучающегося, т.е. развитию умений грамотно и целенаправленно работать с информацией, применяя при ее создании, обработке, передаче и потреблении в том числе и новые информационные технологии, современные технические средства и методы;
– развитию познавательной мотивации, т.е. повышению интереса к предмету, к процессу обучения, активному усвоению учебного материала, развитию способности поднимать и формулировать важные проблемы и вопросы;
– формированию социальной компетентности, т.е. формированию коммуникативных навыков и ответственности за свои знания, способности эффективно общаться с собеседником, решая сложные проблемы и убедительно аргументируя свою точку зрения, уважать чужое мнение.
Вообще, развитие критического мышления ориентировано не на запоминание, а на вдумчивый творческий процесс познания, на постановку проблемы, поиск ее решения, обеспечивает более глубокое усвоение материала, повышает интерес к процессу обучения и к предмету, развивает коммуникативные навыки и др.
Технология развития критического мышления включает в себя три стадии:
– стадия вызова (пробуждение интереса к получению новой информации, актуализация имеющихся у обучающегося знаний, определение целей изучения материала);
– стадия осмысления (содержательная работа обучающегося с текстом, получение новой информации, корректировка обучающимся поставленных целей обучения);
– стадия размышления и рефлексии (формирование личного мнения обучающегося об изученном материале, вывод о достижении цели, коррекция, постановка новых целей обучения) [3].
Остановимся на некоторых методических особенностях реализации каждой стадии.
Традиционно процесс обучения строится, исходя из целей, поставленных преподавателем. Эти цели принимаются студентами в готовом виде как свои собственные. В условиях реализации технологии критического важно добиваться от студентов самостоятельной постановки целей обучения (на первых порах, возможно, с помощью преподавателя).
Кроме того, с целью приобретения дополнительного стимула формулировки студентом собственных целей-мотивов целесообразно предоставить студенту возможность проанализировать то, что он уже знает по изучаемой теме, и помочь ему прийти к выводу о том, что еще необходимо изучить, сформулировав это в виде цели.
Немаловажным аспектом при реализации стадии вызова является систематизация и обобщение всей информации, полученной в результате высказываний студентов. Представив собранную информацию в укрупненном виде, куда могут входить «правильные» и «неправильные» мнения, студенты должны выявить противоречия, нестыковку, непроясненные моменты, которые и определяют направления дальнейшего поиска в ходе изучения новой информации. Причем для каждого из студентов эти направления могут быть индивидуальными. Студент определит для себя, на каком аспекте изучаемой темы он должен заострить свое внимание, а какая информация требует только проверки на достоверность.
Подчеркнем, что стадия вызова и стадия размышления и рефлексии должны быть согласованными между собой: в выборе приемов для занятия должны соблюдаться определенная последовательность и логика. То есть если на этапе вызова применялись «ключевые термины» или «перепутанные логические цепочки», то на этапе рефлексии целесообразно вернуться к выполненным на стадии вызова заданиям и предложить студентам повторно выстроить предложенные события или понятия в хронологической или причинно-следственной последовательности.
В процессе реализации смысловой стадии студенты работают с новой информацией. Преподаватель в процессе усвоения нового материала имеет возможность расставить все акценты в соответствии с ожиданиями и заданными вопросами. Главная задача преподавателя на этом этапе – поддержать активность студентов, их интерес и инерцию движения, созданную во время фазы вызова. Большое значение при этом имеет качество отобранного материала, о котором пойдет речь ниже.
На этой стадии студенты самостоятельно продолжают активно конструировать цели своего учения. Постановка целей в процессе знакомства с новой информацией осуществляется при ее наложении на уже имеющиеся знания. Студенты могут найти ответы на ранее заданные вопросы, решить возникшие на начальном этапе работы затруднения. Вместе с тем далеко не все вопросы могут быть разрешены. В этом случае важно стимулировать студентов к постановке новых вопросов, поиску ответов через контекст той информации, с которой студенты работают.
Работа на стадии осмысления должна быть индивидуальной. Студенты знакомятся с новым материалом. У каждого из студентов знакомство с новым материалом должно происходить в соответствии с поставленными целями, возникшими на стадии вызова. В случае групповой работы должны присутствовать два элемента – индивидуальный поиск и обмен идеями, причем индивидуальный поиск обязательно предшествует обмену мнениями.
В процессе стадии рефлексии та информация, которая была новой, становится присвоенной, превращается в собственное знание. Рефлексивный анализ должен быть направлен на прояснение смысла нового материала, построение дальнейшего маршрута обучения (что понятно, что непонятно, что интересно и т.д.). В процессе обмена мнениями по поводу прочитанного или услышанного студенты должны осознать, что один и тот же текст может вызывать различные оценки, отличающиеся по форме и по содержанию. Некоторые из суждений других студентов могут оказаться вполне приемлемыми для принятия их как своих собственных. На стадии рефлексии осуществляется анализ, творческая переработка, интерпретация изученной информации. Работа может вестись индивидуально, в парах или в группах.
Остановимся на приемах обучения, способствующих развитию критического мышления студентов:
- систематизация материала (графическая): кластеры, таблицы;
- анализ верных и неверных утверждений;
- нахождение логических ошибок и самостоятельное исправление;
- упорядочивание перепутанных логических цепочек;
- установление причинно-следственных связей между блоками информации;
- мозговая атака;
- проблемные вопросы, «толстые» и «тонкие» вопросы;
- методы активного чтения (инсерт, фишбоун, идеал, бортовые журналы и др.);
- обсуждение ошибок в решении задач и проблем (в выборе наиболее рациональных способов решения) путем организации дискуссий и споров;
- рецензирование своих и чужих работ (критический анализ текста);
- тренинги по доказательству, опровержению гипотез и др.
Приведем некоторые типовые примеры заданий, использованных нами в процессе обучения бакалавров педагогического образования математическим дисциплинам:
1. В процессе занятия создается такая ситуация, когда из неверной изначально посылки путем корректных логических суждений получается новый вывод, явно противоречащий имеющимся у студентов знаниям. Предлагается найти причину этого несоответствия.
2. Создается ситуация, в которой из первоначально справедливого суждения путем некорректных логических операций получается абсурдный вывод. Причину предлагается выяснить.
3. Правильный результат специально «критически» осмысливается таким образом, что его правильность оказывается сомнительной (критическое осмысление проводится некорректно). Дальнейшее рассуждение предлагается студентам провести самостоятельно.
4. Провоцирующие задачи: условия содержат упоминания, указания, намеки или другие побудители, подталкивающие студентов к выбору ошибочного пути решения или неверного ответа. Провоцирующие задачи служат средством предупреждения различного рода заблуждений или ошибок обучающихся и показывают необходимость доказательств, рассуждений, с помощью которых студенты контролируют свои действия при решении задач.
5. Кластеры – выделение смысловых единиц текста и графическое их оформление в определенном порядке ввиде грозди. Это педагогическая стратегия, которая помогает студентам свободно и открыто думать по поводу какой-либо темы. Она требует выделения лишь тех структур, которые дают возможность стимулировать размышления о связях между идеями.
6. Инсерт – маркировка текста значками по мере его чтения. Дает возможность обучающемуся увязать содержание текста со своим личным опытом.
7. Синквейн – способность резюмировать информацию, излагать сложные идеи, чувства и представления в нескольких словах – важное умение. Оно требует вдумчивой рефлексии, основанной на богатом понятийном запасе.
8. Фишбоун – «рыбья кость». В «голове» этого скелета обозначена проблема, которая рассматривается в тексте. На самом скелете есть верхние и нижние косточки. На верхних – обучающиеся отмечают причины возникновения изучаемой проблемы. Напротив верхних косточек располагаются нижние, на которых обучающиеся по ходу чтения выписывают факты, отражающие суть.
9. Предлагается сформулировать вопросы к теме в форме «тонких» и «толстых» вопросов и занести их в таблицу. По ходу работы с таблицей в левую колонку записываются вопросы, требующие простого односложного ответа. В правой колонке записываются вопросы, требующие подробного, развернутого ответа; либо вопросы, на которые они сами пока не могут ответить, но хотели бы найти на них ответы.
Приведем конкретные примеры таких заданий:
Пример 1.
Найдите ошибку в доказательстве софизма: 22 = 5. «Возьмем равенство 16 – 36 = 25 – 45. Прибавив к обеим частям равенства по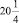 
, получим
.
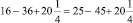Отсюда
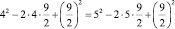
или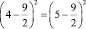 
или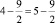 
,
т.е. 4 = 5. Таким образом, 22 = 5».
Пример 2.
Все числа равны между собой в силу следующих рассуждений: Пусть a и b – два произвольно взятых числа, таких, что a ≠ b. Тогда a – b = c или a = b + c. Умножая обе части последнего равенства на (a – b), получим
a(a – b) = (b + c)(a – b),
т.е. a2 – ab = ba – b2 + ca – cb.
Отсюда
a2 – ab – ca = ba – b2 – cb, a(a – b – c) = = b(a – b – c),
т.е. a = b. Таким образом, два произвольных числа равны. Найдите ошибку в приведенных рассуждениях.
Пример 3.
Найдите ошибочные доводы. Катет в прямоугольном треугольнике равен его гипотенузе. Доказательство: Пусть BO – биссектриса угла B. D – середина катета AC. DO ^ AC, OE ^ BC, OF ^ BA. Так как О лежит на биссектрисе угла В, то ΔBFO = ΔBEO (по гипотенузе и острому углу), поэтому
BF = BE. (1)
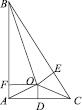
Рис. 1
Далее OA = OC, т.к. каждая точка перпендикуляра к отрезку AC, проходящего через середину отрезка AC, равноудалена от A и C. Так как OF = OE, то ΔAOF = ΔCOE, поэтому
AF = CE. (2)
Складывая почленно выражения (1) и (2), получим BF + AF = BE + CE, т.е. AB = CB. Таким образом, катет равен гипотенузе.
Пример 4.
Какие из приведенных далее определений верные и равносильны: «Треугольник, у которого все стороны равны, называется равносторонним», «Равнобедренный треугольник, у которого один из углов равен 60°, равносторонний», «Треугольник, у которого один из углов равен 60°, называется равносторонним».
Пример 5.
Верно ли умозаключение «Каждая призма – многогранник. Следовательно, каждая правильная призма – правильный многогранник»?
Пример 6.
Где ошибка в рассуждениях?
«Полупустое = Полуполное»,
значит
«
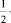Пустое = 
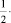Полное».
Если равны половинки, то равны и целые, т.е. «Пустое = Полное»
Пример 7.
Даны пять слов: четыре объединены одним общим признаком, пятое к ним не подходит. Его нужно подчеркнуть.
- а) степень;
б) одночлен;
в) произведение;
г) тождество;
д) соотношение;
- а) двучлен;
б) многочлен;
в) степень;
г) коэффициент;
д) уравнения;
- а) линейное уравнение;
б) график;
в) прямая;
г) система;
д) квадрат суммы двух выражений;
- а) кратное
б) НОК
в) НОД
г) делитель
д) дробь;
- а) задача;
б) уравнение;
в) переменная;
г) число;
д) функция.
Пример 8.
Из данной последовательности удалите лишний элемент:
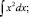
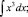
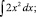
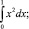
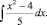
Пример 9.
Найти и исправить ошибки.
Достоверное событие – событие, которое в результате испытания может произойти, а может и не произойти. Невозможное событие – событие, которое вообще не может произойти в результате испытания. Случайное событие – событие, которое обязательно происходит в результате испытания. Несовместные (несовместимые) события – события, которые могут произойти одновременно в результате испытания.
Резюмируя, отметим, что формирование критического мышления дает студенту: повышение эффективности восприятия информации, интереса как к изучаемому материалу, так и к самому процессу обучения; ответственность за собственное образование; умение работать в сотрудничестве; повышение качества образования; желание и умение учиться в течение всей жизни. А также акцент на формировании критического мышления студентов дает преподавателю: умение создать в группе атмосферу открытости и ответственного сотрудничества; возможность использовать модель обучения и систему эффективных методик, которые способствуют развитию критического мышления и самостоятельности в процессе обучения; стать практиками, которые умеют грамотно анализировать свою деятельность; стать источником ценной профессиональной информации для других преподавателей.
Таким образом, критическое мышление набирает силу и укрепляет свои позиции. Причем применение критического мышления все чаще рассматривается как необходимость и одно из главных условий перестроения образования, начиная от содержания и заканчивая образовательными стандартами, а также внедрением новых прогрессивных форм и методов обучения.
Библиографическая ссылка
Бронникова Л.М. РАЗВИТИЕ КРИТИЧЕСКОГО МЫШЛЕНИЯ СТУДЕНТОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН // Современные наукоемкие технологии. – 2016. – № 3-1. – С. 101-105;URL: https://top-technologies.ru/ru/article/view?id=35700 (дата обращения: 20.04.2024).