Пневматические роботы нашли широкое применение в машиностроительном производстве. Они используются во многих технологических процессах и операциях: штамповки, резки, механической сборки, монтаже, сварке и др. Пневматические роботы, в отличие от электромеханических, дешевы, компактны, безопасны, обладают высокой надежностью и высоким ресурсом работы, перепрофилирование производства с использованием пневматических роботов доступнее. Одной из распространенных и актуальных задач, возникающих при автоматизации производства, является позиционирование рабочих органов роботов с заданной точностью и быстродействием, с конечной целью обеспечения заданных показателей качества технологического процесса.
Решение этой задачи заключается в создании рациональных конструкций пневматических робототехнических механизмов, с параллельным совершенствованием способов программного управления ими, или с учетом информации о среде, или управления функционально законченными действиями, или с применением самообучаемых моделей функционирования на основе искусственного интеллекта.
В данной работе рассмотрена методика формирования управляющих программ робота на основе нечетких коэффициентов, позволяющих гибко управлять пневмодвигателями робота. Приведены результаты экспериментов.
Основная часть
Разработанная аппаратно-программная система управления пневматическим роботом с использованием крановых превмораспределителей (КПР) на основе нечеткой логики показана на рис. 1. Работа системы основана на адаптивном программном управлении, с использованием нечеткой логики на основе отслеживаемых данных от датчиков обратной связи (измерители пути) магнитострикционного типа. Для обеспечения приемлемых расходов газа и высоких динамических характеристик пневмоприводов робота используются крановые превмораспределители с приводом от электрических шаговых двигателей (Патент RU 158927 U1. 2016 бюл. № 2), конвертирующих прямоугольные импульсы электрического напряжения в механическое вращение. За рабочие положения каждого пневмопривода отвечает пара КПР, за исключением пневмопривода механизма захвата, в нем используется один КПР. В качестве регулятора давления также применен КПР с управлением от электрического шагового двигателя, обратная связь в нем осуществляется при помощи датчика давления пьезоэлектрического типа.
Обучаемая программная часть системы включает следующие блоки.
«Блок обучения» получает данные с датчика обратной связи и фактически управляет «блоком элементарных программ управления». Эти данные формируют базу знаний, на основе которой формируются управляющие правила. Эти правила также могут задаваться или изменяться на основе команд, задаваемых в экспертном режиме.
Функционирование базы знаний нечеткого контроллера осуществляется на трех уровнях. На первом уровне располагаются лингвистические переменные, используемые для фаззификации данных. Лингвистические переменные формируются экспертным путем в «блоке задания параметров режимов работы робота» и методами прямых измерений при помощи магнитострикционного датчика измерителя пути. На этом уровне определяется базовый диапазон и число нечетких меток на нем, а также тип функции принадлежности. Количество нечетких меток влияет на точность управления.
На втором уровне сохранены нечеткие правила управления, применяемые для преобразования задаваемых параметров в управляющие. Эти правила составляются из лингвистических переменных, определенных на уровне выше.
На третьем уровне осуществляется соответствие полученных правил с реальными элементарными командами управления блока числового программного управления, которые сохраняются в блоке «База данных программ задания режимов работы робота» и в дальнейшем исполняются «блоком элементарных программ управления».
Разработка программы работы системы управления роботом на основе нечеткой логики включает несколько этапов.
В начале экспертным путем задаются режимы работы – типовой характер работы робота на основе элементарных программ управления.
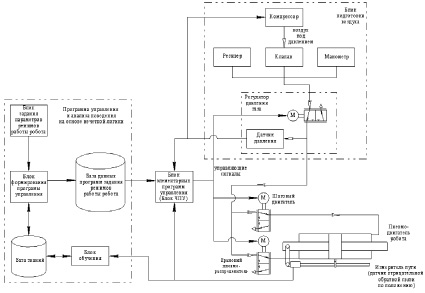
Рис. 1. Схема системы управления пневматическим роботом
На втором этапе, на основе характеристической методики работы робота, формируются изменения параметров во времени.
Следующий этап включает получение множества экспериментальных данных параметров (L, a1, a2) работы робота в соответствии с технологическим процессом по перемещению деталей разной массы. Для примера в таблице приведены данные с перемещаемой полезной нагрузкой, равной 0,1 кг.
Пример таблицы параметров L, a1, a2
|
L, м |
0 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,1 |
0,11 |
0,12 |
0,13 |
0,14 |
0,15 |
0,16 |
0,17 |
0,18 |
0,19 |
0,2 |
|
a1, град |
12,5 |
12 |
11,5 |
11 |
10,5 |
10 |
9,5 |
9 |
8,5 |
8 |
7,5 |
7 |
6,5 |
6 |
5,5 |
5 |
4,5 |
4 |
3,5 |
3 |
0 |
|
a2, град |
0 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
9,5 |
10 |
10,5 |
11 |
11,5 |
12 |
12,5 |
На четвертом этапе проводится фаззификация, то есть преобразование четких экспериментальных значений входных переменных в нечеткие с использованием лингвистического описания параметров (L, a1, a2).
Построение систем нечеткого вывода основано на понятии лингвистической переменной:
⟨X, U, FL(x), Stx(x), Sem(x)⟩, (1)
где X – название конкретного параметра (L, a1, a2); U – базовое множество диапазона значений параметров L, a1, a2; FL(x) – нечеткие метки; Stx(x) – синтаксические правила формирования команд управления; Sem(x) – семантические множества, показывающие отношения лингвистических переменных друг на друга.
Лингвистическая переменная L – это линейная длина измерительного элемента – волновода, датчика измерителя пути. Разбиваем показания L на нечеткие метки – 21 точку (0; 0,01; 0,02; 0,03; …; 0,2 м), a1, a2 – углы поворота шаговых двигателей КПР рассматриваемого привода.
Связь между базовым множеством параметров и нечеткими метками осуществляется при помощи функций принадлежности. Совместное рассмотрение лингвистических переменных L, a1, a2 лучше всего описывается треугольными (для L) и гауссовыми (для a1, a2) функциями принадлежности.
В аналитическом виде треугольная функция принадлежности может быть задана следующим образом [1]:
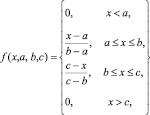 , (2)
, (2)
где x – базовое значение; b – нечеткая метка, соответствующая вершине распределения; a – левая граница функции принадлежности; с – правая граница функции принадлежности.
В аналитическом виде симметричная Гауссова функция принадлежности может быть задана следующим образом:
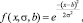 (3)
(3)
где b – координата максимума функции принадлежности; σ – коэффициент концентрации функции принадлежности.
Далее на основе лингвистических переменных формируются нечеткие фреймы управления типа ЕСЛИ L ТО a1 И a2.
На основе полученных фреймов формируется база знаний:
ЕСЛИ Lниз ТО a1выс И a2низ.
ЕСЛИ Lниже сред ТО a1выше сред И a2ниже сред.
ЕСЛИ Lсред ТО a1сред И a2сред.
ЕСЛИ Lвыше сред ТО a1ниже сред И a2выше сред.
ЕСЛИ Lвыс ТО a1низ И a2высок.
С их помощью получаем приближенный нечеткий результат.
Заключительный этап – дефаззификация, то есть приведение нечетких фреймов управления реальным управляющим командам, которые записываются и хранятся в БД.
Проведем дефаззификацию по методу Мамдани.
Выходная переменная относительно одной лингвистической переменной определяется как:
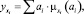 (4)
(4)
где х – четкое значение переменной A; yxi – выходная переменная y относительно лингвистической переменной A; аxi – нечеткие метки, принадлежащие лингвистической переменной А; μx(аxi) – принадлежность переменной х к соответствующей нечеткой метке.
Тогда выходные данные для a1, a2 запишем
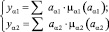 (5)
(5)
или
Таким образом, четкий вывод будет рассчитываться как сумма произведений переменных с добавлением дополнительной метки направления:
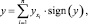 (7)
(7)
где y – четкое выходное значение; yxi – выходная переменная относительно соответствующей лингвистической переменной; n – количество лингвистических переменных; sign(y) – метка сигнатуры направления движения, определяется по приращению относительно двух точек, пройденных пневмодвигателем.
Метка сигнатуры направления необходима для преодоления точки равновесия a1 и a2, а также она применяется для записи сопутствующих физических данных.
В дальнейшем значение y учитывается в командах управления роботом верхнего и нижнего уровня.
На рис. 2 приведено окно визуализации нечеткого логического вывода.
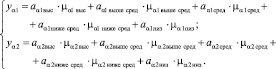 (6)
(6)
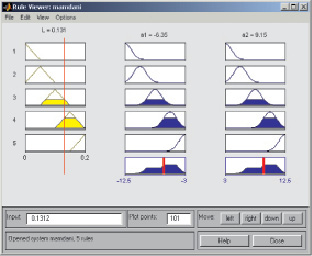
Рис. 2. Визуализация нечеткого логического вывода в среде Matlab
Результаты экспериментов
Испытания подтвердили работоспособность модели; разработана экспериментальная установка на базе пневматического робота МП-9С с применением предлагаемой аппаратно-программной системы управления и проведены экспериментальные исследования ее динамических характеристик; погрешность позиционирования рабочего органа робота при рабочей нагрузке 0,1 кг составила ~ 0,14 мм (или 0,1 %) при доверительной вероятности 0,993. Проведено сравнительное исследование с существующим аналогом, показавшее, что при использовании предлагаемой системы управления и в зависимости от заданной программы работы повышается быстродействие при достижении конечных положений выходных звеньев робота, возможна регулировка скорости, а также позиционирование рабочего органа робота в промежуточных положениях за счет программного управления шаговыми двигателями; установлено, что быстродействие предложенной системы управления выше на 16,7 % по сравнению с системой с использованием ближайшего аналога.
Выводы
Предлагаемая система управления пневматическим роботом на основе нечеткой логики позволяет управлять пневмоприводом робота по разностному способу включения крановых регулирующих устройств за счет программного управления их приводами, – электрическими шаговыми двигателями, с использованием методов нечеткой логики; повысить качество процесса управления пневматическим роботом за счет управляемого регулирования этапов замедления и ускорения при достижении промежуточных положений приводов его исполнительных механизмов с погрешностью не более 0,1 %.
Библиографическая ссылка
Хазиев Э.Л., Хазиев М.Л. СИСТЕМА УПРАВЛЕНИЯ ПНЕВМАТИЧЕСКИМ РОБОТОМ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ // Современные наукоемкие технологии. 2016. № 3-1. С. 74-78;URL: https://top-technologies.ru/ru/article/view?id=35695 (дата обращения: 04.02.2026).



