Вибрационные машины широко применяются в различных отраслях техники для интенсификации физических и химических процессов, для транспортирования и дозирования сыпучих материалов, их смешивания, уплотнения, а также разделения сыпучих материалов на разнокачественные фракции в качестве самостоятельной машины или в составе технологической линии [1]. Вибрационные сепарирующие машины используются для обогащения полезных ископаемых, вибрационной обработки деталей, изготовления литейных форм и выбивки опок, разделение различного рода порошков, подготовки сырья в технологических процессах производства строительных изделий и пищевых производств, сепарирования зерна на элеваторах, подготовке семян в агропромышленном комплексе [2].
В зависимости от назначения данные машины отличаются друг от друга по типу привода, по числу и расположению колеблющихся ситовых корпусов, по характеру их движения.
По типу преобразования подводимой энергии в энергию механических колебаний привода вибрационных машин делятся на две группы: с кинематически жестким приводом и инерционными колебателями направленного действия [3]. Простейшими из них являются кинематически жесткие приводы. Достоинство кинематически жесткого привода заключается в том, что он обеспечивает заданную амплитуду колебаний рабочего органа при изменении частоты колебаний, колеблющейся массы и технологической нагрузки. Недостатком такого привода является действие больших инерционных сил на звенья устройства и, следовательно, вибрация несущей конструкции вибрационной машины, снижение надежности машины, вибрация основания, на которое установлена машина [4, 5].
В вибрационных сепарирующих машинах вибрация рамы влияет не только на амплитуду колебаний ситовых корпусов, но и на равномерность толщины слоя материала по ширине сита. Наложение вибрации рамы на колебания ситовых корпусов вызывает поперечную вибрацию машины, в результате которой сепарируемый материал перераспределяется на одну сторону. При увеличении амплитуды наложенных поперечных колебаний увеличивается неравномерность толщины слоя по ширине сита, изменяется характер движения компонентов по ситу, движение осуществляется без мгновенных остановок, увеличивается путь зерна по ситу [6]. Все эти аспекты отрицательно влияют на технологические показатели работы машины.
При всем многообразии расчетных методов и вариантов их применения к пространственным стержневым конструкциям в литературе отсутствуют комплексные решения оптимизации сложных несущих конструкций машин, учитывающие ограничения по виброхарактеристикам, минимизирующие жесткость и массу конструкции, учитывающие влияние виброперемещений несущей конструкции на качество выполнения технологического процесса.
Существующие методы расчетов позволяют оптимизировать отдельные несложные элементы конструкций или определять максимальные напряжения в разработанных пространственных конструкциях и оценивать ее прочностные характеристики.
Для того чтобы на стадии проектирования задать оптимальные сечения элементов и их структурное расположение с учетом ограничений по виброхарактеристикам при минимальной массе конструкции, необходима разработка комплексной математической модели оптимизации таких конструкций [7]. Сложность задачи заключается также в том, что применение различных дополнительных устройств для снижения вибрации, а также повышение жесткости конструкции за счет дополнительных элементов приводит к увеличению массы самой машины. Для сепарирующих машин, которые устанавливаются, как правило, на перекрытиях строительных конструкций, это приводит к увеличению нагрузки на перекрытия, дополнительной вибрации перекрытия, что в свою очередь приводит к увеличению стоимости строительной части зданий и сооружений [8, 9, 10].
Цель исследования. Для определения оптимальных кинематических параметров работы вибрационных сепарирующих машин, оптимизации жесткости несущего основания на стадии проектирования необходимо определение собственных частот колебаний несущей конструкции вибрационной машины, а также оценка влияния конструктивных особенностей и компоновочных решений на собственные частоты несущей конструкции.
Материалы и методы исследования
Рассмотрим одну из наиболее характерных схем несущей рамной конструкции вибрационной сепарирующей машины. Данная конструкция может быть представлена как несимметричная рама с заделанными стойками, нагруженная двумя сосредоточенными массами (рис. 1). Под сосредоточенными массами подразумевается нагружение рамы со стороны подвесок ситовых корпусов вибрационной машины.
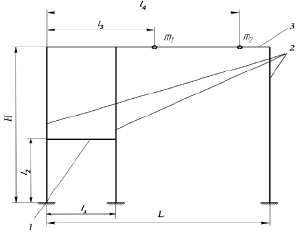
Рис. 1. Схема для расчета частот собственных колебаний рамной конструкции: 1 – горизонтальная балка с моментом инерции I1 = 88,35·10–8 м4; 2 – вертикальные балки (I2 = 87,88·10–8 м4); 3 – горизонтальная балка (I3 = 29,96·10–8 м4)
Пренебрегая собственной массой системы, прикладываем силы инерции в места приложения масс m1 и m2. Для системы с двумя степенями свободы выражение для определения частот принимает следующий, известный в теории колебаний, вид:
l1·(m1d11w2 – 1) + l2m2d12w2 = 0;
l1m1d21w2 + l2·(m2d22w2 – 1) = 0, (1)
где l – амплитуда колебаний, м; dik – перемещение в направлении i, вызванное единичной силой, действующей в направлении k, м; w – частота собственных колебаний, рад/с.
Учитывая, что амплитуда при наличии колебаний не обращается в нуль, определитель, состоящий из коэффициентов системы уравнений, равен нулю. В развернутом виде определитель представляется уравнением
w4·(d11d22 – d122)·m1m2 – – w2·(d11m1 + d22m2) + 1 = 0. (2)
Используя метод сил, для определения перемещений от единичных нагрузок строим эпюры изгибающих моментов под действием единичных сил Р1 = 1 и Р2 = 1, приложенных в точках расположения грузов. Значения перемещений dik определяются при помощи правила Верещагина и теоремы о взаимности перемещений (теорема Максвелла).
Результаты исследования и их обсуждение
Решение уравнения (2) осуществлялось в программе «МАТНCAD-2001». Были получены первая и вторая частоты собственных колебаний несущей рамной конструкции, которые составили соответственно 110 и 185 рад/с. Расчеты проведены для следующих размеров и сосредоточенных масс: L = 2,27 м; l1 = 0,4 м; l2 = 0,9 м; l3 = 0,80 м; l4 = 1,47 м; H = 1,59 м; m1 = 85 кг; m2 = 100 кг.
Величина значений виброперемещений несущей конструкции зависит от величины собственных частот конструкции. Согласно уравнению (2) на величину собственных частот оказывает влияние величина сосредоточенных масс и перемещение балки под действием грузов с массами m1 и m2 (рис. 1), а также перемещение в направлении силы тяжести от массы m1 под действием массы m2. Значения данных перемещений зависят от точек приложения этих масс. При смещении масс к центру увеличиваются прогибы и возрастает безразмерный коэффициент динамичности, т.е. отношение динамического перемещения к статическому:
K∂ = 1/|(1 – p2/w2)|, (3)
где р – частота возмущающей силы, рад/с.
Зависимость динамического коэффициента от точки приложения груза массой m1 при постоянном значении величины l4 представлена на рис. 2 (кривая 1). Зависимость динамического коэффициента от точки приложения груза массой m2 при постоянном значении величины l3 представлена на рис. 2 (кривая 2). Максимальное значение коэффициент динамичности принимает при одновременном приложении масс к центру конструкции, он соответствует значению 1,778, тогда как при исходной схеме он равен 1,261. При этом увеличение коэффициента динамичности составляет 40 %. При максимальной удаленности друг от друга данных грузов коэффициент динамичности уменьшается на 10 %.
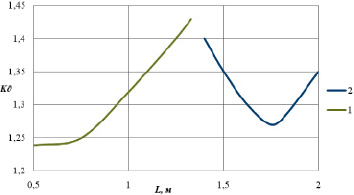
Рис. 2. Зависимость коэффициента динамичности (k∂) от точек приложения масс: 1 – для груза с массой m1; 2 – для груза с массой m2
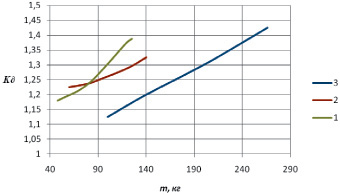
Рис. 3. Зависимость коэффициента динамичности (k∂) от величины масс (m1, m2): 1 – для груза с массой m1; 2 – для груза с массой m2; 3 – для двух грузов с суммой масс m1 + m2
Исследуем зависимость частоты колебаний от величины масс, приложенных к данной конструкции. При увеличении какой-либо массы все собственные частоты уменьшаются, что приводит к увеличению динамического коэффициента. Зависимости динамического коэффициента от величины массы грузов приведены на рис. 3. Увеличение массы m1 на 40 % вызывает увеличение динамического коэффициента на 5 % (кривая 1). При увеличении массы m2 на 47 % значение динамического коэффициента возрастает на 9,5 % (кривая 2). Одновременное увеличение масс вызывает максимальный рост динамического коэффициента. При увеличении суммы масс на 43 % динамический коэффициент возрастает на 13,2 % (кривая 3).
Заключение
Приведенные данные свидетельствуют о том, что на виброперемещение несущей конструкции вибрационной сепарирующей машины оказывает существенное влияние величина и положение сосредоточенных масс. Наиболее значимым фактором является положение масс. При расположении масс в середине верхней горизонтальной балки значение ее виброперемещения в вертикальном направлении возрастает на 40 %. При увеличении массы системы за счет увеличения сосредоточенных масс собственные частоты уменьшаются, а виброперемещения возрастают (для случая, когда вынужденные частоты колебаний меньше собственных).
Библиографическая ссылка
Пивень В.В., Уманская О.Л. ОПТИМИЗАЦИЯ НЕСУЩЕЙ КОНСТРУКЦИИ ВИБРАЦИОННОЙ МАШИНЫ // Современные наукоемкие технологии. 2016. № 3-1. С. 70-73;URL: https://top-technologies.ru/ru/article/view?id=35694 (дата обращения: 09.03.2026).



