А<p><img src="/i/2016/3-1/lomakina05_fmt.jpg" alt="lomakina05.wmf" /></p>В работе рассматривается диагностирование сложных систем произвольной физической природы, в том числе и программных средств, модель которых может быть представлена в виде графа или таблицы функции неисправностей. Вершины графа, в частности, могут изображать блоки системы.
Диагностирование системы, т.е. определение ее неисправных блоков, производится на основании концепции скрытого параметра. В задаче диагностирования вектор проверок b и результата тестирования системы y являются наблюдаемыми параметрами. Вектор состояния системы s – неизмеряемое свойство системы, от которого зависит наблюдаемый параметр y. Данный вектор s является скрытым параметром. Скрытый параметр можно определить, определив его функцию на множестве наблюдаемых параметров.
С целью построения оптимальной стратегии локализации дефектов в работе используется метод главных компонент. Данный метод позволяет выбрать оптимальную по информационному критерию последовательность точек контроля для каждого блока системы. Использование индивидуальных последовательностей точек контроля для каждого блока позволяет локализовать неисправность более точно, чем использование единой последовательности точек контроля, полученной на основе усредненного информационного критерия.
Метод определения состояния системы
Пусть G(V, U) – упорядоченный граф с n вершинами, представляющий модель объекта диагностирования [3]. Обозначим V – множество вершин графа, U – множество ребер графа. Вершины графа соответствуют модулям объекта, а ребра графа – связям между модулями. Обозначим через X = {x1, ..., xq} (q ≤ n) множество входов графа G(V, U), а через W = {w1, ..., wp} (1 ≤ p) – множество выходов.
Если в объекте диагностирования в некоторый момент времени одновременно отказало некоторое множество модулей, то совокупность номеров {η1, ..., ηk} соответствующих вершин графа G, представляющего модель объекта диагностирования, назовем дефектом кратности k (1 ≤ k ≤ n).
Пусть имеет место дефект {η1, ..., ηk}. Состоянием объекта диагностирования назовем n-мерный вектор s = {s1, ..., sn}, в котором

Всего будет 2n состояний объекта. Всё множество состояний S можно рассматривать как пространство элементарных событий s ∈ S, каждое из которых может наступить после эксплуатации системы в течение заданного времени с вероятностью, равной
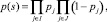
где pj – вероятность появления дефекта в j-м модуле; J – множество номеров исправных модулей; I – множество номеров неисправных модулей.
При этом предполагается, что дефект в одном из модулей не влияет на вероятность появления дефектов в других модулях.
Будем полагать, что вершины x и r в графе G(V, U) образуют контрольную пару (x, r), если в соответствующей системе сигнал, подаваемый на вход элемента x, может быть снят на выходе элемента r. Очевидно, для того чтобы пара (x, r) была контрольной, необходима достижимость вершины r графа G(V, U) из вершины x. В дальнейшем контрольную пару будем называть точкой контроля, а множество точек контроля обозначим Z.
Вектором проверки точки контроля (x, r) назовем n-мерный вектор
b(x, z) = {b1, ..., bn}
компонента bl которого равна 1, если существует хотя бы один путь от x к r, содержащий вершину l, и равна 0 в противном случае.
Пусть для упорядоченного графа G(V, U) на n вершинах задано некоторое исходное множество Z точек контроля. Тогда матрицей проверок
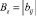
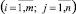
на множестве Z точек контроля назовем матрицу, в которой
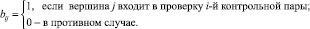
Проверка сигнала в каждой точке контроля позволяет судить о работоспособности всех модулей соответствующего подмножества, которое определяется совокупностью единиц в соответствующей строке матрицы проверок.
Результатом диагностирования системы, содержащей m точек контроля, будет являться m-мерный вектор y = {y1, ..., ym}, для которого выполняется соотношение: y = Bs. Матрица В является математической моделью канала связи между множеством векторов состояний объекта S и множеством векторов результатов диагностирования Y. Компоненты вектора y равны 1, если значение измеряемого параметра в соответствующей точке контроля вышло из допуска и равны 0 в противном случае. Таким образом, при выходе из строя одного из модулей вектор y совпадает с соответствующим столбцом матрицы проверок. В случае выхода из строя нескольких модулей с номерами η1, ..., ηk вектор y равен логической поэлементной сумме соответствующих столбцов матрицы:
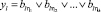
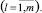
Концепция скрытого параметра
Изначально понятие скрытого параметра было введено в квантовой механике для разрешения парадоксов [6]. Для того чтобы разрешить квантовые неопределенности, было сделано предположение о существовании неизвестных свойств объектов, влияющих на наблюдаемые параметры. Эти свойства были названы скрытыми параметрами. В качестве примера рассмотрим периодическую систему химических элементов Менделеева. Ранее метод построения этой системы являлся скрытым параметром, поскольку правила классификации химических элементов были неизвестны. Поскольку критерием классификации является заряд ядра, то количественной характеристикой скрытого параметра является количество протонов в ядре атома. Наблюдаемыми параметрами являются результаты химических реакций – новые вещества.
В данной работе предлагается использовать концепцию скрытого параметра в области проектирования систем диагностирования состояния сложных систем.
Пусть система описывается множеством наблюдаемых параметров O. Будем полагать, что элементом o ∈ O множества наблюдаемых параметров является векторная величина o = {o1, …, on+1}, компоненты o1, …, on которой равны соответствующим компонентам вектора проверки b, а on+1 равен результату тестирования системы y. Таким образом, вектор o представляет собой конкатенацию вектора b и скаляра y. Поскольку результат тестирования системы может принимать одно из двух значений, то множество наблюдаемых параметров O будет содержать 2m элементов, где m – число точек контроля.
В задаче диагностирования вектор проверки b и результат тестирования системы y являются наблюдаемыми параметрами, а вектор состояния системы s – неизмеряемое свойство системы, которое является скрытым параметром. Зададим функцию скрытого параметра, возвращающую результат тестирования заданного блока:
s = f(o1, …, on),
где o1, …, on – точки контроля, проверяющие заданный блок.
Рассмотрим пример поиска дефекта во втором блоке системы, состоящем из пяти блоков. Из всего множества наблюдаемых параметров O были выбраны четыре параметра – o1, …, o4, которые позволяют обнаружить неисправность во втором блоке. Значение скрытого параметра – состояния системы s – будет определяться из соотношения y = Bs (рис. 1). Наблюдаемые параметры выбираются таким образом, чтобы доставлять максимальное количество информации о состоянии системы – локализовать неисправность с точностью до наименьшего подмножества. Каждый новый параметр будет доставлять дополнительную информацию о состоянии системы, таким образом уменьшая подмножество блоков, подозреваемых на наличие дефекта.
Таким образом, каждый наблюдаемый параметр o характеризует значение скрытого параметра с точностью до некоторого подмножества. Совместное использование набора наблюдаемых параметров позволит более точно локализовать скрытый параметр (рис. 2).
Таким образом, концепция скрытого параметра позволяет определить последовательность точек контроля для проверки наличия дефекта в каждом блоке системы.
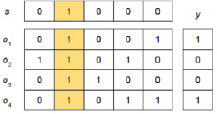
Рис. 1. Соответствие между состоянием системы s и результатом тестирования y
Рис. 2. Соответствие между множеством результатов тестирования Y и множеством состояний системы S
Использование метода главных компонент для выбора оптимального числа точек контроля
Рассмотрим возможность сокращения числа наблюдаемых параметров с использованием метода главных компонент.
Объект диагностирования можно представить в виде многомерного объекта, характеризующегося вектором значений признаков. В задаче диагностирования признаком может служить точка контроля b. Таким образом, значением признака будет являться результат тестирования объекта на основании выбранной точки контроля. Результат тестирования системы на основании m точек контроля можно представить в виде m-мерной векторной переменной y ∈ Y.
Продолжительность тестирования системы возрастает с ростом размерности обрабатываемых данных. Время диагностирования можно уменьшить, если подвергнуть снижению размерность пространства признаков. Снижение размерности возможно, поскольку результаты тестирования объекта могут быть взаимосвязаны. Взаимосвязь между результатами тестирования указывает на избыточность полученных данных с точки зрения теории информации.
Снижение размерности m-мерного исходного пространства точек контроля Y без существенной потери информации о состоянии системы позволит сократить продолжительность тестирования системы без снижения точности локализации дефекта. Для снижения размерности воспользуемся методом главных компонент. Алгоритм будет заключаться в последовательном отборе точек контроля на основе концепции скрытого параметра. Критерий останова алгоритма основан на методе главных компонент и позволяет получить минимальную последовательность точек контроля, доставляющую максимальное количество информации о состоянии выбранного блока. Сформулируем процедуру выбора точек контроля для каждого блока системы.
Рассмотрим пример работы алгоритма при выборе последовательности точек контроля для поиска неисправности в первом блоке (табл. 1).
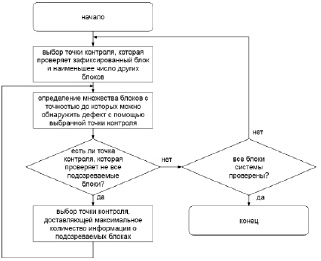
Рис. 3. Блок-схема алгоритма выбора точек контроля
Таблица 1
Результат работы алгоритма выбора точек контроля
|
Номера итерации |
Выбранная точка контроля |
Множество блоков, состояние которых проверяет выбранная точка контроля |
Результат тестирования системы |
Множество блоков, подозреваемых на наличие дефекта после тестирования |
|
1 |
a |
{1, 3, 4} |
1 |
{1, 3, 4} |
|
2 |
b |
{1, 2, 4, 6} |
1 |
{1, 4} |
|
3 |
c |
{4} |
0 |
{1} |
Таблица 2
Результаты работы безусловного алгоритма
|
Номер итерации |
Выбранная точка контроля |
Множество блоков, состояние которых проверяет выбранная точка контроля |
Результат тестирования системы |
Множество блоков, подозреваемых на наличие дефекта после тестирования |
|
1 |
a |
{1, 3, 4} |
1 |
{1, 3, 4} |
|
2 |
b |
{1, 2, 4, 6} |
1 |
{1, 4} |
|
3 |
d |
{3, 5, 6} |
0 |
{1, 4} |
Выбранные три точки контроля позволяют локализовать дефект с точностью до блока. Данную процедуру необходимо повторить для остальных блоков системы. Таким образом, результатом работы алгоритма будет пять последовательностей точек контроля. Последовательность проверки блоков системы зависит от вероятности отказа блоков. Если вероятность отказа блоков различна – следует проверять блоки в порядке убывания вероятности их отказов. Если априорной информации о вероятности отказов блоков нет – тогда порядок проверки блоков не важен.
Сравним безусловный алгоритм, предложенный в [3], с данным алгоритмом. Результатом работы безусловного алгоритма является последовательность точек контроля для обеспечения максимальной глубины локализации дефекта. Последовательность точек контроля, полученная с помощью безусловного алгоритма, такова: {1, 3, 4}, {1, 2, 4, 6}, {3, 5, 6}. Проверим систему на основании данных точек контроля, полагая, что первый блок системы неисправен (табл. 2).
Безусловный алгоритм позволил локализовать дефект с точностью до двух блоков.
Условный алгоритм, предложенный в данной статье, позволяет определить последовательности точек контроля для получения информации о конкретном блоке. Безусловный алгоритм, предложенный в [3], определяет последовательность точек контроля, которые доставляют максимальное количество информации о состоянии системы в среднем.
Применение предложенного условного алгоритма для проверки каждого блока системы позволяет последовательно исправлять однократные дефекты и, таким образом, точнее локализовать состояние системы, чем использование безусловного алгоритма.
Выводы
На основании концепции скрытого параметра и метода главных компонент был разработан алгоритм диагностирования сложных систем. Предложенный алгоритм позволяет определить минимальную последовательность точек контроля для обеспечения максимальной глубины локализации дефекта. Результаты экспериментальных исследований подтвердили более высокую эффективность разработанного алгоритма диагностирования сложных систем по сравнению с безусловным алгоритмом.
Библиографическая ссылка
Ломакина Л.С., Ворон А.М. ДИАГНОСТИРОВАНИЕ СЛОЖНЫХ СИСТЕМ НА ОСНОВЕ КОНЦЕПЦИИ СКРЫТОГО ПАРАМЕТРА // Современные наукоемкие технологии. 2016. № 3-1. С. 50-54;URL: https://top-technologies.ru/ru/article/view?id=35690 (дата обращения: 09.03.2026).



