Преобразования, происходящие в жизни современного информационного общества, быстрая смена технологий в результате достижений фундаментальных и прикладных исследований создают потребности различных областей науки и техники в профессионале, мыслящем нестандартно, способном принимать решения и нести за них ответственность. Важную роль в подготовке такого специалиста играет система образования как одна из фундаментальных устойчивых форм социального института, обеспечивающая целостность и стабильность преемственности социального опыта.
В современном образовании, в условиях компетентностного подхода целенаправленное использование концепции учебных моделей научных исследований способствует ранней диагностике способностей и склонностей обучаемых к научной деятельности на основе универсальных умений и навыков математического и компьютерного моделирования. Развитие творческих способностей и черт личности обучаемых, связанных с потребностью к самообразованию и самовоспитанию, обеспечивается соответствием содержания учебной модели научного исследования уровню знаний учащихся и их возрастным особенностям [1].
Научная и исследовательская деятельность – это творческая деятельность, и не существует общих универсальных правил или схем, по которым она развивается. Но все же, несмотря на это, специалисты в области изучения исследовательского поведения пытались и пытаются выработать приемы и алгоритмы, которые позволяют отыскивать истину.
Одну из наиболее удачных, а потому и наиболее известных разработок такого рода создал в XIX веке известный математик Б. Больцано. Он выделил приемы эвристической деятельности, которые называл «искусство открытия»: точно сформулировать вопрос, ответ на который мы ищем (необходимо строго ограничивать область исследования); оценить, является ли истинный ответ на поставленный вопрос возможным с точки зрения имеющихся знаний; разбить задачу на подзадачи и подвопросы и искать ответы на них сначала выведением решения из известных истин или сведением к решению подобных задач; прямо вывести решение из уже имеющихся знаний, если это возможно; выдвинуть гипотезы методом полной или неполной индукции или аналогии; совокупность четвертого и пятого приемов; сопоставить полученный результат с известными знаниями; проверить точность использования логических приемов; проверить правильность всех определений и суждений, используемых в решении; выразить все понятия решаемой задачи в «целесообразных» знаках (воспользовавшись символическим языком); стремиться к выработке наглядных образов объектов задачи; результат решения формулировать логически строго; оценить все «за» и «против» полученного результата; решать с большим сосредоточением на задачу [6].
В методике учебно-исследовательской деятельности речь идет о получении новых знаний в общекультурном значении. Путь, который самостоятельно проходит молодой исследователь, «переоткрывая» какой-либо факт, для него может быть столь же сложным, новым и творческим, как и для первооткрывателя. Результат исследовательской деятельности во многом зависит от той проблемы, которую предстоит решить. Многие задачи изначально носят чисто учебный характер. Некоторые фундаментальные проблемы имеют внутренний потенциал, позволяющий получить объективно новое знание. Иногда учебная задача помогает увидеть новую проблему, выходящую за рамки учебной.
Аналитический метод (решение задач по формулам), сыграл важную роль в развитии науки ХVIII–XX вв. и широко применяется в настоящее время. Однако метод все же является ограниченным, поскольку его можно использовать, как правило, в идеализированных ситуациях. Аналитические задачи обычно разбираются в задачниках по физике и математике. Это нужные задачи, так как они обучают мыслить математическими и физическими категориями, но они, как правило, далеки от реальности. Они идеализированы настолько, что могут служить только иллюстрацией закона, правила или иерархии моделей. В таких задачах приходится считать зависимости предельно простыми: движения- равноускоренными, силы – линейно зависящими от отклонений или от скорости, токи – линейно зависящие от напряжения, оптические среды – однородными.
Со времен натурфилософии Ньютона совершенствовались численные методы в дискретной математике, которые позволяют приближенно решать задачи математического моделирования. В идейном плане численные методы проще аналитических методов высшей математики, и некоторые из них доступны школьникам [5].
Вспоминая историю науки, отметим, что в 50–60-х годах XX века началась новая научная революция – достижения физики, математики, информатики и техники открыли перспективы реализации крупнейших проектов – овладение атомной энергией и создание атомного оружия, освоение космического пространства и поиск новых фундаментальных законов природы. Осуществление проектов потребовало огромных затрат ресурсов, детального анализа возможных путей протекания физических явлений и технологических процессов, тщательного отбора наилучших вариантов постановки дорогостоящих экспериментов. Сложность возникающих задач делала их недоступными для стандартных приемов теоретической и экспериментальной физики, а необходимость решения проблем стимулировала возникновение вычислительной физики как новой методологии научных исследований.
В начале ХХ века внимание многих ученых было привлечено к различным задачам физики твердого тела. Их интересовало, можно ли предсказывать теплоемкость твердых тел на основе простых представлений о движении и взаимодействии отдельных частиц, как в кинетической теории газов. Проблема хаотизации колебаний атомов в нелинейном кристалле восходит к работам П. Дебая (1914 г.).
Позднее Э. Ферми были инициированы первые вычислительные эксперименты в физике твердого тела. Когда в 1953 году ученые сформулировали проблему, они думали, что удастся найти решение путем расчета на компьютере. Научные исследования проводились на Mathematical Numerical Integrator and Computer (MANIAC), одном из первых цифровых компьютеров в мире. Однако теплового равновесия в системе так и не удалось достигнуть.
Дж. Паста и С. Улам рассчитывали динамику 32 и 64 связанных осцилляторов с нелинейными силами взаимодействия. Вместо термализации энергии, хаотизации колебаний обнаруживался квазипериодический обмен энергии между нормальными модами и солитонные решения. Кроме того, наблюдался парадокс возврата системы к начальному состоянию. Совокупность изучаемых вопросов численного моделирования о применимости законов статистической физики к нелинейным системам с большим числом степеней свободы стали называть классическими проблемами или парадоксами Ферми-Паста-Улама (ФПУ) [10].
Методике учебного компьютерного моделирования при изучении фундаментальных научных проблем посвящены работы с участием автора [5], [6], [7], [8], [9].
Вероятностный характер законов классической статистической физики, где случайность была налицо, принято было списывать на очень большое число частиц и степеней свободы и на неполноту данных. Такая точка зрения со временем стала привычной и позволяла как-то примириться с этим противоречием, но, тем не менее, оставляла чувство неудовлетворенности. Поэтому неопровержимое установление возможности, хаотического, непредсказуемого поведения детерминированных динамических систем, а также применимость законов статистической физики в модели ФПУ решающим образом затрагивает наши фундаментальные мировоззренческие представления о природе волновых процессов в нелинейных средах.
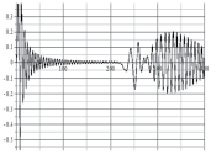
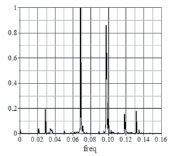
Рис. 1. Спектральный анализ в нелинейной цепочке связанных осцилляторов
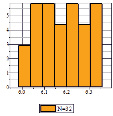
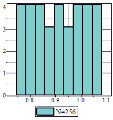
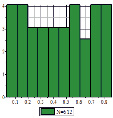
Рис. 2. Гистограммы равномерного распределения энергии по степеням свободы в цепочке Ферми-Паста-Улама
На рис. 2 представлены результаты компьютерных экспериментов с цепочкой Ферми-Паста-Улама разного размера со статистической обработкой данных. Современное программное и математическое обеспечение, интерактивная графика позволяют выйти за рамки классической системы ФПУ и получить гистограммы равномерного распределения энергии по степеням свободы в малой окрестности средних значений для длинных наноразмерных цепочек.
В учебном пособии [2] феноменологическая термодинамика рассматривается как универсальная модель физической системы. Показано существование термического уравнения состояния из транзитивности термодинамического равновесия. Причем уравнения транзитивности всегда можно определить, мысленно разбивая рассматриваемую физическую систему на макроскопические подсистемы. Поэтому существенное увеличение размера цепочки оправдано, причем, внесение случайностей в динамику детерминированной системы возможно за счет взаимодействия цепочки с окружающей средой, а также за счет возможных случайных погрешностей вычислительного эксперимента. В этом случае статистический закон о равномерном распределении энергии по степеням свободы можно обобщить на случай произвольной молекулярной системы c учетом дисперсии измеряемой энергии.
Выводы
Реальный мир управляется не детерминистическими законами, но и не абсолютной случайностью. Устойчивые и обратимые во времени системы соответствуют предельным, исключительным случаям. Адекватное физическое описание хаотических систем, эволюции во времени достижимо только на уровне ансамблей. Здесь опять торжествует парадоксальный характер управляющих миром законов, соединяющий воедино, казалось бы, несовместимые представления. Но эта несовместимость на поверку оказывается результатом слишком узких рамок теории – соответствующее обобщение показывает, что противоречивость положений выступает только в крайних, предельных случаях, когда старая теория соответствует наблюдаемым реалиям и пропадает в новой теории, основанной на других фундаментальных концепциях [3].
Выявление и развитие творческого потенциала учащихся может быть достигнуто путем реализации концепции учебной модели научного исследования при изучении фундаментальных проблем математического и компьютерного моделирования реальных процессов и систем. Соответствие научной значимости учебной модели и дидактических принципов доступности и наглядности может быть обеспечено путем построения и изучения относительно простых моделей сложных явлений при последовательном учете иерархии пространственно-временных масштабов, характеризующей процессы в реальных системах.
В рамках развития современного компетентностного подхода в образовании можно говорить об определенных универсальных исследовательских умениях и навыках, связанных с возможностью реализации цикла научного творчества, независимо от конкретного объекта исследования применительно к проведению комплексных теоретико-экспериментальных исследований по разработке физических, математических и компьютерных моделей изучаемых явлений, проведение вычислительного эксперимента и анализ полученных результатов с целью адекватного объяснения парадоксов и возможностей решения актуальных проблем, обсуждаемых в научной и методической литературе.
Библиографическая ссылка
Ходанович А.И. КЛАССИЧЕСКИЕ ПАРАДОКСЫ ВЫЧИСЛИТЕЛЬНОЙ ФИЗИКИ В СОВРЕМЕННОЙ НАУКЕ И ОБРАЗОВАНИИ // Современные наукоемкие технологии. 2016. № 2-3. С. 585-588;URL: https://top-technologies.ru/ru/article/view?id=35679 (дата обращения: 31.01.2026).



