Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дулесов А.С. 1 Карандеев Д.Ю. 1 Кондрат Н.Н. 1

---

1 ФГБОУ ВПО «Хакасский государственный университет им. Н.Ф. Катанова»

Представлен метод, с помощью которого определяется количество информации, содержащееся в структуре технической системы. Для реализации метода даны пояснения, касающиеся подготовки исходных данных. Данные формируются на основе составленной структуры и её показателей. Показателями структуры являются вероятности состояний элементов системы, которые разделены по качественному признаку на два противоположных состояния. Построены математические выражения, и представлен порядок расчетов определения информационной энтропии. В основу метода положен способ построения последовательно-параллельных структур методом минимальных путей. Дан пример, на котором показана работа данного метода. Предлагаемый метод позволяет на основе сопоставления значений энтропии противоположных состояний выбрать систему с более высоким уровнем эффективности или структурной надежности. Полученные результаты сравнивались с данными, полученными методом перебора состояний системы.

Статья в формате PDF

0 KB

мера информации

информационная энтропия

структура технической системы

1. Дулесов А.С., Агеева П.А. Мера информации в задаче оценки бесперебойной работы технической системы // Журнал «Фундаментальные исследования». – 2011. – № 12 (часть 1). – С. 102–107.

2. Дулесов А.С., Карпушева Т.В., Хрусталев В.И. Информационные взаимосвязи в технических системах и оценка качества информации // Журнал «В мире научных открытий». – 2010. – № 6 (12). – С. 56–61.

3. Дулесов А.С., Кондрат Н.Н. Количество информации при наложении и пересечении элементарных событий // Журнал «Научное обозрение». – 2014. – № 12. – С. 146–150.

4. Дулесов А.С., Кондрат Н.Н. Мера неопределенности информации и её свойства применительно к оценке случайного поведения технического объекта // Журнал «Научное обозрение». – 2014. – № 7. – С. 258–264.

5. Дулесов А.С., Кондрат Н.Н. Определение для простейшей структуры технической системы количества информационной энтропии посредством её нормировки // Журнал «Фундаментальные исследования». – 2015. – № 2 (часть 20). – С. 4408–4412.

6. Дулесов А.С., Кондрат Н.Н. Определение количества информационной энтропии в структуре технической системы методом перебора состояний // Журнал «Фундаментальные исследования». – 2015. – № 7 (часть 4). – С. 745–748.

7. Дулесов А.С., Кондрат Н.Н. Эквивалентирование количества информационной энтропии в структуре технической системы // Журнал «Фундаментальные исследования». – 2015. – № 6 (часть 1). – С. 14–19.

8. Дулесов А.С., Семенова М.Ю., Хрусталев В.И. Свойства энтропии технической системы // Журнал «Фундаментальные исследования». – 2011. – № 8 (часть 3). – С. 631–636.

Многие технические системы имеют явно выраженные структуры с вероятностными характеристиками. Отображение структуры, например, в виде графа, применение математических инструментов определения количества информации, позволяет оценивать состояния системы. По величине информации можно судить о том, насколько информативна система. О количественном содержании информации в технической системе можно ознакомиться в работах [1, 2, 8].

Элементы системы связаны между собой определенным образом. И от того, какие требования предъявляются к системным элементам, как они связаны между собой, в каких состояниях они находятся в тот или иной момент времени, зависит не только топология структуры, но и количество информации. Например, рассматривая структурную надежность системы, разделяют состояния элементов на работоспособное и неработоспособное, что предопределяет необходимость рассчитывать количество информации (информационной энтропии) по качественному признаку [5].

Определение количества энтропии требует построения моделей выявления совместной и условной энтропий при рассмотрении событий, обусловливающих вероятностные состояния элементов. Такие модели предложены в [3, 4]. Реализация моделей требует разработки методов. Одним из таких методов можно считать метод перебора состояний (предложенный в [6]), метод эквивалентирования последовательно-параллельных структур (представленный в [7]). Однако такие методы неприменимы для сложнозамкнутых и многоэлементных структур. Поэтому востребован метод, который базировался бы на способе построения минимальных путей от начала к концу структуры.

Далее предложим к рассмотрению математический метод минимальных путей, который позволит выполнить расчет количества энтропии, присущей противоположным (непересекающимся) вероятностным состояниям элементов системы.

Предварительная подготовка данных востребована для расчета количества энтропии и включает в себя построение (например, согласно [3, 4]) статистического ансамбля. В качестве статистических показателей могут присутствовать: время, в течение которого элемент находился в том или ином состоянии; частота появления тех или иных событий и др. Эти показатели позволяют рассчитать вероятности pi нахождения элемента i в рассматриваемом состоянии и найти собственное значение информации элемента: 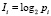. Логарифм определения величины Ii в битах имеет основание, равное 2, что свидетельствует о рассмотрении двух противоположных состояний (например, работоспособное и неработоспособное, рассматриваемые при анализе структурной надежности технической системы). Поэтому в нашей задаче будем учитывать только 2 противоположных состояния, в предположении о наличии качественной составляющей, касающейся необходимости разделения значений собственных (частных) информаций Ii на две составляющие. Собственная информация с учетом её разделения на составляющие позволяет определить информационную (статистическую) энтропию по Шеннону. Так для одного элемента i энтропия определится по выражению:

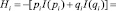
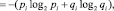(1)

при условии pi + qi = 1. Здесь pi и qi соответственно, – вероятность работоспособного и неработоспособного состояний элемента i.

Для всей системы в целом можно получить суммарную энтропию:

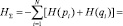
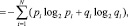(2)

где N – число элементов в структуре системы. При всех pi = qi = 0,5, по (2) получим энтропию: HΣ = N.

Применение (2) дает частное решение, поскольку не учитывается топология структуры, и самое главное, нет возможности выделить энтропию противоположных состояний для последующего более полного анализа. Чтобы устранить данный недостаток, востребован предлагаемый в работе метод, позволяющий рассчитывать качественные составляющие суммарной энтропии. Имея на предварительном этапе предобработанные данные, можно приступить к определению энтропии методом минимальных путей.

Определение энтропии методом минимальных путей. Для определения энтропии каждого из двух противоположных (непересекающихся) множеств состояний элементов необходимо, с одной стороны, иметь число элементов N (состояния которых рассматриваются как независимые), с другой – топологию структуры.

Метод предполагает рассмотрение структуры, как правило, замкнутой, с обозначением в ней начала (исходной точки) и конца (конечной точки) для поиска и выделения минимальных путей. Методика построения минимальных путей известна, с ней можно ознакомиться в материалах, представленных в сети Интернет.

Сформированные пути в виде последовательно-параллельной структуры являются основанием для применения предлагаемого метода, который базируется на эквивалентных преобразованиях [7]. Предложим далее порядок и математические выражения для определения энтропии вновь созданной структуры системы. Отметим дополнительно: представленные далее в выражениях подстрочные символы справедливы при условии нумерации путей и перенумерации элементов каждого пути.

1. Рассчитывается энтропия по каждому из N элементов согласно (1):

– для работоспособного состояния элемента i –

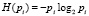; (3)

– для неработоспособного состояния элемента i –

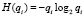. (4)

2. Для каждого пути определяются вероятности:

– работоспособного состояния элементов пути j –

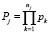, (5)

где pk – вероятность работоспособного состояния элемента k, пути j, nj – количество элементов, входящих в путь;

– неработоспособного состояния элементов пути j –

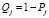. (6)

3. По каждому из путей определяются составляющие энтропии:

– работоспособного состояния элементов пути j –

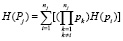; (7)

– неработоспособного состояния элементов пути j –

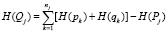. (8)

4. Определение энтропии системы:

– работоспособного состояния –

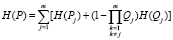, (9)

где m – количество путей;

– неработоспособного состояния –

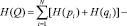
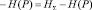, (10)

где i – порядковый номер элемента структуры системы.

При реализации данного метода имеется один нюанс, а именно: последовательно-параллельная структура, состоящая из путей, не является эквивалентом исходной структуры. Следовательно, появляются проблемы в получении приемлемого решения. Во-первых, количество элементов в последовательно-параллельной структуре будет больше чем в исходной структуре, во-вторых – из-за того, что учитываются только минимальные пути, результат будет с погрешностью по отношению к результатам, полученным методом перебора всех состояний элементов. Первая проблема имеет решение, вторая зависит от уже сложившегося на практике подхода к построению последовательно-параллельных структур.

Разрешение первой проблемы заключается в следующем. Каждый из элементов в созданной последовательно-параллельной структуре будет дублирован один и более раз. Поскольку такая структура является только расчетной, то количество информации в ней должно быть равно количеству энтропии исходной структуры. Тогда определить энтропию элемента k (вновь созданной структуры) следует по выражениям:

;

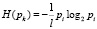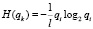, (11)

где l – количество повторений элемента i во вновь построенной структуре, i – порядковый номер элемента исходной структуры.

Пример. Следует определить количество энтропии работоспособного и неработоспособного состояний мостиковой структуры, представленной на рис. 1.

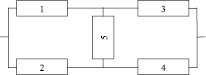
Рис. 1. Мостиковая структура (схема)

Согласно рис. 1 множество всех состояний элементов 52 = 32. Работоспособных состояний или путей – 16: {13}, {24}, {154}, {253}, {134}, {243}, {123}, {124}, {524}, {123}, {1524}, {1523}, {1534}, {2534}, {1324}, {12345}. Из них минимальными являются пути {13}, {24}, {154}, {253}, количество которых – m = 4. Последовательно-параллельная структура из минимальных путей представлена на рис. 2.

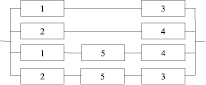
Рис. 2. Последовательно-параллельная структура (схема)

Примем значения вероятностей: pi = 0,9; qi = 1 – pi = 0,1. Такие значения вероятностей приняты исходя из возможности сопоставления полученных значений, с результатами, представленными в [7].

Порядок выполнения расчетов выполним без перенумерации элементов каждого из путей, представленных на рис. 2.

1. Определим по (3) и (4) энтропию элементов исходной схемы с N = 5 (рис. 1):

– для работоспособного состояния –

,

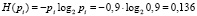– для неработоспособного состояния –

.

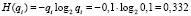Поскольку в последовательно-параллельной структуре (рис. 2) элементы дублированы (каждый элемент дублирован дважды – l = 2), то для определения энтропии её элементов применим выражения (11):

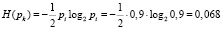
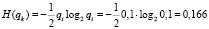
2. По выражениям (5) и (6) определяем для каждого из путей вероятности:

– работоспособного состояния: , ,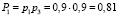

, ,

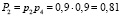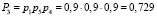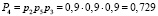– неработоспособного состояния: , , , .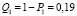

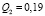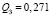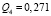3. Согласно (7) и (8) определим составляющие энтропии каждого пути:

– работоспособного состояния:

,

,

,

,

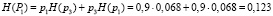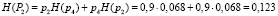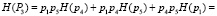
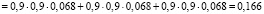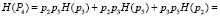
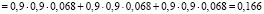– неработоспособного состояния:

,

,

,

.

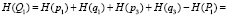
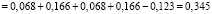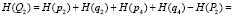
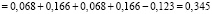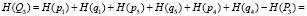
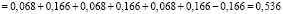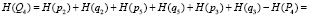
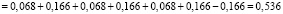4. Определение по выражениям (9) и (10) энтропии системы:

– работоспособного состояния:

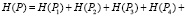
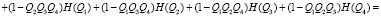
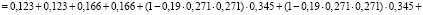
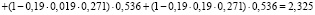
– неработоспособного состояния:

.

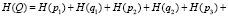
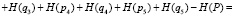
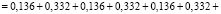
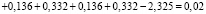Из расчетов видно, что энтропия работоспособного состояния преобладает над энтропией противоположного состояния, поскольку вероятность работоспособного состояния выше, чем неработоспособного.

Сравним аналогичные результаты с представленными в работе [7]: Н(Р) = 2,169; Н(Q) = 0,176; суммарная энтропия – НΣ = Н(Р) + Н(Q) = 2,345.

Поскольку оба сравниваемых метода построены на предположении о независимости событий (возникающих в системе), то полученные по ним суммарные энтропии совпали, подтверждая тем самым справедливость предлагаемого метода. Однако между энтропиями состояний существует разница (между Н(Р) – 6,7 %, между Н(Q) – 8,8 раз). Ошибка обусловлена способом построения минимальных путей, без учета множества других путей. Представленный метод можно рекомендовать для систем с высоким показателем работоспособности элементов.

Заключение

Основное назначение данного метода – определение энтропии двух противоположных состояний системы. Результаты могут быть получены для последовательно-параллельных структур систем и для замкнутых структур через их преобразование по методу минимальных путей. Полученное количество энтропии отражает качественное и количественное содержание информации. С помощью полученных математических выражений можно рассчитывать количество информации отдельно по каждому из рассматриваемых противоположных (например, для работоспособного и неработоспособного) состояний системы. Интеграция данного метода в среду оценки состояния системы (например, её структурной надежности) через меру неопределенности информации позволит выполнить сопоставительные оценки между противоположными состояниями системы.

Рассматривая различные варианты структур системы, используя предлагаемый метод, можно выбрать более надежную или эффективную структуру с позиции наличия в ней определенного количества информационной энтропии.

Работа выполнена при поддержке гранта РФФИ № 15-08-01473а.

Библиографическая ссылка