Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сарванова Ж.А. 1

---

1 ФГБОУ ВПО «Мордовский государственный педагогический институт им. М.Е. Евсевьева»

В статье представлен один из возможных путей решения проблемы обучения учащихся методу площадей при решении геометрических задач в контексте деятельностного подхода. Обучение решению задач в контексте указанного подхода предполагает раскрытие деятельности поиска их решения, разъяснение различных приемов и методов. Учащиеся испытывают трудности в применении метода площадей, особенно при решении заданий итоговых экзаменов по математике. Поэтому выделение приемов, составляющих названный метод, формирование адекватных им действий, является актуальным. Автор указывает типы геометрических задач, для которых использование метода площадей наиболее рационально. Каждому такому типу поставлены в соответствие приемы решения. Рассмотрены примеры геометрических задач, направленных на формирование отдельных действий выделенных приемов и их совокупностей.

Статья в формате PDF

0 KB

деятельностный подход

формирование приемов

метод площадей

геометрическая задача

решение задач

соответствующие действия

1. Капкаева Л.С. Алгебраический и геометрический методы в школьном курсе математики как способы познавательной деятельности учащихся// Гуманитарные науки и образование. – 2012. – №1 (9). – С.18–22.

2. Капкаева Л.С. Интеграция алгебраического и геометрического методов в среднем математическом образовании: монография; Мордов. гос. пед. ин-т. – Саранск, 2004. – 287 с.

3. Овчинникова Е.Е. Использование метода площадей и объемов при решении школьных геометрических задач: дис. ... канд. пед. наук. – М., 2002. – 133с.

4. Родионов М.А., Федосеев В.М., Шабанов Г.И. Актуализация социокультурной проекции математического образования как фактор его гуманитаризации// Интеграция образования. – 2012. – №2. – С.91–95.

5. Саранцев Г.И. Методика обучения геометрии: учеб. пособие для студентов вузов по направлению «Педагогическое образование». – Казань: Центр инновационных технологий, 2011. – 228с.

6. Сарванова Ж.А. Совокупность задач для обучения учащихся основной школы применению метода площадей при решении геометрических задач// Учебный эксперимент в образовании. – 2015. – №4 (76). – С.34–39.

7. Сарванова Ж.А. Элективный курс по геометрии «Метод площадей» для учащихся 10–11 классов// Преподавание математики в школах и вузах: проблемы содержания, технологии и методики: сборник научных трудов IV Всероссийской научно-практической конференции, Глазов, 14–15 декабря 2012г. – Глазов. – С.118–120.

8. Ульянова И.В. Обучение учащихся доказательству теорем в контексте деятельностной концепции УДЕ// Наука и школа. – 2010. – №4. – С. 85–88.

9. Ульянова И.В. Особенности обучения учащихся методам решения геометрических задач в контексте укрупнения дидактических единиц// Знание. Понимание. Умение. – 2012. – №1. – С.233–238.

Обучение математике на современном этапе базируется на использовании системно-деятельностного подхода, заключающегося в создании условий для организации активной учебно-познавательной деятельности обучающихся, т.е. обучении школьников способам рассуждений, самостоятельному открытию фактов, их обоснований [4, с.91]. Существуют и другие точки зрения на содержание понятия деятельностного подхода в обучении. Согласно одной из них, деятельностный подход соотносят с выделением совокупности действий, адекватных понятию, теореме, методам решения задач [8, с.85].

При обучении решению задач деятельностный подход предполагает раскрытие деятельности поиска решения, разъяснение используемых приемов и методов [2, c.72]. Однако применение данного подхода к обучению учащихся осложняется тем, что недостаточно полно выделен деятельностный состав многих методов решения задач, в частности метода площадей. Ктому же круг задач школьных учебников геометрии, направленных на применение метода площадей в различных ситуациях, ограничен. Поэтому выделение приемов, составляющих указанный метод, раскрытие их содержания, области применения, способов формирования является актуальным.

Цель исследования – выделить частные приемы, составляющие метод площадей, их деятельностные компоненты, выявить средства их формирования.

Материалы и методы исследования

Анализ научно-методической литературы по проблемам обучения учащихся методам решения задач, использования деятельностного подхода в обучении; анализ школьных учебников геометрии; изучение и обобщение педагогического опыта.

Результаты исследования и их обсуждение

В методике обучения математике выделены гносеологические и деятельностные компоненты метода.

К гносеологическим компонентам относят: исходные знания об объекте, к которому применяется метод, его свойствах; знания, полученные в ходе преобразования или изучения объекта; знания о сфере приложения метода (круг задач, решаемых с помощью данного метода, их виды и т.д.); знания об особенностях его использования в зависимости от сферы приложения [1, c.21].

К деятельностным компонентам относят определенную систему действий, реализация которой ведет к достижению результата; средства осуществления деятельности, основанной на данной системе действий. Отмечается, что обучение методу связано не только с усвоением школьниками деятельностных и гносеологических компонентов, но и собучением применению метода [1, c.22].

Л.С.Капкаева поясняет, что любой метод состоит из приемов, но не является их простой суммой. Например, метод треугольников состоит из приемов, основанных на использовании признаков равенства треугольников, свойствах равнобедренного треугольника и т.д. [1, с.20].

Общий подход к обучению решению задач геометрическими методами рассмотрен в работах многих авторов. Так, Г.И.Саранцев утверждает, что методы решения задач, особенно геометрических, состоят из различных действий (логических, специальных, эвристических), поэтому применение метода предполагает овладение составляющими его действиями и их совокупностями.

К действиям, составляющим метод координат, он относит:

1)перевод геометрического языка задачи на аналитический и обратно;

2)построение точки по заданным координатам;

3) нахождение координат заданных точек;

4)вычисление расстояния между точками, заданными координатами;

5)оптимальный выбор системы координат;

6)составление уравнения заданных фигур;

7)видение за уравнением конкретного геометрического образа;

8)выполнение преобразования соответствующих алгебраических соотношений [5, c.133].

Средством формирования действий и их совокупностей, по мнению автора, должны выступать соответствующие задачи.

Конкретизация общего подхода рассмотрена в работах И.В.Ульяновой, Е.Е.Овчинниковой и др. Вработах И.В.Ульяновой говорится об использовании в обучении методам решения задач укрупненного подхода к формированию составляющих их действий. Суть последнего заключается в том, что у учащихся нужно последовательно формировать новые действия при одновременном закреплении ранее сформированных. Средством реализации указанного подхода выступают блоки укрупненных задач [9, с.235].

В диссертации Е.Е.Овчинниковой выделены следующие действия, выполняемые в процессе решения задач методом площадей и объемов:

1)анализ заданной в условии задачи конфигурации в целом и отдельно ее элементов с точки зрения включения площади или объема для решения задачи;

2)отбор элементов заданной конфигурации, которые будут необходимы для опредмечивания выбранных свойств площадей или объемов;

3)выбор конкретных свойств и формул площади или объема, связанных с заданной конфигурацией;

4)нахождение площади или объема выбранных фигур или тел, их отношения;

5)подстановка найденных значений или отношений в выбранные свойства для получения результата [3, с.53].

Отметим, что выделенные действия относятся не только к методу площадей, но и к методу объемов, то есть носят обобщенный характер.

Автором выделены три типа задач на применение указанного метода, то есть по сути указана гносеологическая составляющая метода. Первый тип задач характеризуется нахождением площади фигуры двумя способами, составления уравнения и нахождения неизвестной величины. Ко второму относятся задачи, в решении которых используется свойство аддитивности площади. Задачи на применение свойств отношения площадей – это задачи третьего типа. Характерной чертой таких задач является то, что площадь может быть включена в условие или требование задачи, а может и не фигурировать в них [3, c.52]. Поэтому площадь фигуры выступает вспомогательным элементом при их решении, что и вызывает определенные трудности у учащихся. Тем не менее применение именно метода площадей позволяет наиболее рационально, «красиво» решать многие задачи, в том числе и задачи итоговых экзаменов по математике.

Опираясь на имеющиеся исследования, а также на действия, применяемые в решении задач с использованием метода площадей, нами были выделены частные приемы, образующие метод площадей и составляющие их действия. Под приемом деятельности понимают наиболее рациональную совокупность действий и операций, выполняемых в определенном порядке и служащих для решения задач деятельности [1, c.20]. Тогда прием решения задачи можно определить как наиболее рациональную совокупность действий, выполняемых в определенном порядке и способствующих выполнению ее требования.

Приемы, составляющие метод площадей, поставим в соответствие тем типам задач, которые были указаны выше. Таким образом, можно выделить прием, основанный на нахождении площади фигуры двумя способами, прием, основанный на использовании свойства аддитивности площади и прием, основанный на использовании свойств отношений площадей и соответствующих отрезков.

Проиллюстрируем применение метода площадей на примерах решения задач, в условии которых говорится о треугольнике. Отметим, что выделенные действия будут справедливы и для решения названных выше типов задач, в содержании которых фигурируют не только треугольники, но и другие геометрические фигуры.

Итак, прием, основанный на нахождении площади фигуры двумя способами, составляет совокупность следующих действий:

1)составление выражения для площади фигуры по условию задачи;

2)составление выражения для площади фигуры с использованием неизвестного элемента;

3)составление равенства полученных выражений для площади фигуры;

4)решение полученного уравнения и нахождение неизвестной в задаче величины.

Приведем примеры задач1–3 для формирования перечисленных действий.

Задача1. Втреугольнике со сторонами a и b высота, проведенная к первой стороне, равна h. Обозначьте высоту, проведенную ко второй стороне треугольника, за x и найдите площадь треугольника двумя способами.

Задача2. Втреугольнике со сторонами 9 и 6 высота, проведенная к первой стороне, равна 4. Используя формулу площади треугольника, cоставьте уравнение.

Задача 3. Утреугольника АВС к стороне АВ=9 проведена высота СН=4. Кстороне АС проведена высота ВM=6. Найдите сторону АС.

Задача1 направлена на формирование действий (1) и (2). Решение задачи2 включает выполнение действий (1)(3).

Выполняя решение задачи3, используя формулу площади треугольника

S=0,5⋅a⋅h,

находят площадь треугольника АВС одним способом, то есть

S=0,5⋅АВ⋅СН.

Затем находят площадь этого же треугольника другим способом, а именно

S=0,5⋅АС⋅ВM.

Далее приравнивают найденные выражения

0,5АВ⋅СН=0,5⋅АС⋅ВM,

откуда

АВ⋅СН=АС⋅ВM,

ирешают уравнение

6⋅АС=36,

откуда АС=6. Таким образом, решение задачи3 способствует формированию всего комплекса действий, составляющих первый прием. Причем приведенная последовательность задач характеризуется тем, что каждой из задач1 и 2 является вспомогательными для решения задачи3. Такая цепочка задач полезна не только для поэтапного формирования отдельных действий приема, их совокупности, но и способствует открытию учащимися способа решения задач.

Укрупнив рассматриваемый прием, мы получим прием, основанный на использовании свойства аддитивности площади. Перечислим действия, адекватные этому приему:

1)разбиение фигуры на части с использованием условия (требования) задачи;

2)составление выражения для площадей фигур, получившихся при разбиении (для этого используем данные и искомые элементы задачи);

3)составление выражения для площади фигуры как суммы площадей составляющих ее фигур;

4)нахождение площади исходной фигуры, используя данные задачи;

5)составление равенства полученных выражений для площади фигуры;

6)решение полученного уравнения и нахождение неизвестной в задаче величины (или вывод доказываемого равенства).

Названные действия можно выполнять в указанной последовательности. Однако некоторые их них, например действия (2), (3) и (4), можно выполнять в любом порядке. Также можно заметить, что действия (3)(6) названного приема аналогичны действиям, составляющим первый прием.

Приведем примеры задач4–6, направленных на формирование действий, выделенных во втором приеме.

Задача4. На стороне AC треугольника АВС отмечена точка М. Используя эту точку, разбейте данный треугольник на два треугольника, не имеющих общих внутренних частей, и выразите площадь треугольника АВС через площади полученных треугольников.

Задача5. Вравностороннем треугольнике АВС точка М – середина стороны АС. Из точки М к сторонам АВ и ВС проведены соответственно перпендикуляры MH и MK. Докажите, что

ВМ=MH+MK.

Задача6. Докажите, что сумма расстояний от любой точки, выбранной на основании равностороннего треугольника, до его боковых сторон есть величина постоянная.

Задача4 направлена на формирование действий (1)(3).

В решении задачи5 разбиваем треугольник АВС на два треугольника АВM и ВМС. Тогда, используя свойство аддитивности площади, получим

SABC=SАВМ+SВМС,

то есть

0,5⋅ВМ⋅АС=0,5⋅MH⋅АВ+0,5⋅MK⋅ВС

или

ВМ⋅АС=MH⋅АВ+MK⋅ВС,

откуда, учитывая равенство сторон треугольника, получаем

ВМ=MH+MK.

Таким образом, учащиеся будут выполнять действия (1)(6), составляющие второй из приведенных приемов. Отметим, что задачи4 и 5 являются вспомогательными для задачи6.

В основу третьего приема положим действия, выполняемые при использовании свойств отношений отрезков и площадей, указанных в работе [3].

Свойство1. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).

Свойство2. Если треугольники имеют общую сторону, то их площади пропорциональны длинам отрезков, высекаемых продолжением их общей стороны на прямой, соединяющей их вершины.

Согласно этому свойству S1:S2=m:n (рисунок).

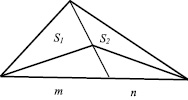
Иллюстрация свойства 2

Свойство3. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.

Применение указанных свойств при решении задач позволило нам выделить состав приема, основанного на отношении площадей и соответствующих отрезков. Перечислим входящие в него действия:

1)соотнесение искомых отрезков с площадью фигур, элементами которых они являются (или соотнесение площадей искомых фигур с соответствующими отрезками), и применение свойств1–3;

2)нахождение отношения площадей этих фигур (длин отрезков).

Приведем примеры задач7–9, способствующих формированию данного приема.

Задача7. Докажите, что каждая медиана треугольника разбивает его на две равновеликие части.

Задача8. Докажите, что медианы треугольника разбивают его на шесть равновеликих частей.

Задача9. Втреугольнике ABC на стороне AB выбрана точка D так, что AD:DB=1:2. На стороне ВС – точка E, такая, что BE:EC=1:2. Какую часть площади треугольника ABC составляет площадь треугольника DBE?

В задаче7 применяется свойство1. Задачу8 можно решить, применяя либо свойство1, либо свойство2. При решении задачи9 отношение площадей треугольников ABC и DBE соотносят с отношениями отрезков AD и DB, BE и EC, заданных в условии задачи. Затем применяют свойство3, так как треугольники имеют общий угол, и после небольших преобразований, получают SDBE:SABC=1:3. Таким образом, выполняются все действия названного приема.

Заключение

Применение метода площадей при решении геометрических задач способствует развитию творческого, эвристического мышления учащихся, поскольку использование площади как вспомогательного элемента – это нестандартный, эвристический способ решения задач. Формирование последовательности действий, составляющих выделенные нами приемы, будет способствовать эффективному и осмысленному применению метода площадей в различных ситуациях. Средством обучения учащихся этому методу являются геометрические задачи определенных типов. Один из вариантов построения совокупности таких задач в контексте темы исследования приведен нами в статье [6]. Там же можно найти и методику поэтапного формирования действий, адекватных методу площадей [6]. Кроме того, формирование целостной системы знаний о данном методе можно продолжить на занятиях элективного курса по геометрии. Примерное содержание такого курса приведено нами в статье [7].

Библиографическая ссылка