Сегодня трудно представить себе проектную или конструкторскую организацию, не использующую в своей практике в той или иной мере математические модели. Все более распространенным и эффективным становится применение математического моделирования в научных исследованиях. Интенсивно разрабатываются математические модели в экономике, управлении, биологии и многих других областях знаний. Математическое моделирование в последние десятилетия оформилось в отдельную междисциплинарную область знаний с присущими ей объектами, подходами и методами исследования. Под моделью (от лат. modulus – мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект-оригинал, сохраняя некоторые важные для данного исследования типичные его черты. Процесс построения и использования модели называется моделированием. Системой моделирования занимались А.А. Самарский, Н.Н. Моисеева [4] и др.
Моделирование является одним из составных компонентов наглядно-модельного обучения. В процессе обучения мы формулируем модель существенных признаков объекта изучения, адекватных поставленной цели. Важно до предъявления объекта изучения предварительно провести подготовку обучаемого к восприятию, четко поставить цель, предъявить объект изучения и организовать деятельность обучаемого при работе с объектом адекватно знаково–символическим средствам представления математических знаний.
Наглядно-модельное обучение включает в себя как построение модели, так и формирование адекватного результата внутренних действий бакалавров в процессе учебной деятельности. Модель должна отражать суть понятия, формы или метода исследования.
Степень сложности задачи, как об этом пишет А.М. Матюшкин [3], определяется числом существенных взаимосвязей в ее условии, числом опосредований и преобразований, приводящих к нахождению искомого. Зависит она и от уровня самостоятельности при постановке и решении проблемы (В.А. Крутецкий [2]).
Моделирование позволяет максимально полно отразить существенные качества объекта исследования, при этом предполагается процедура научного анализа, при которой происходят последовательные многократные дополняющие друг друга взаимодействия теоретических схем с эмпирическими данными, что существенно облегчает выработку системы операциональных понятий, хорошо согласованных как с категориями методологического уровня, так и с экспериментальными данными.
Метод моделирования предполагает определение структуры и свойств изучаемого явления в виде модели с заданными параметрами. Модель строится путем последовательного формирования мотивации и сопоставления результатов функционирования этой модели с экспериментально наблюдаемыми процессами. При существенном расхождении смоделированных и реально наблюдаемых процессов необходимо искать аналитически пропущенные в модели элементы и корректировать ее параметры. Построение математической модели позволяет экспериментально согласовать с помощью единого формализованного описания все взаимосвязанные виды проявления мотивации. С помощью метода моделирования преодолевается односторонний подход к пониманию, диагностике и формированию мотивации: двойственность во взаимосвязи понятий мотивации и предметности снимается, так как эти феномены представляются свойствами единого образования. На основе специально разработанной процедуры эмпирического измерения экспериментально выделенных формализованных параметров этой модели каждому испытуемому можно дать комплексную характеристику, спрогнозировать направление измерений мотивации, выработать рекомендации по ее формированию, изучить условия и факторы, влияющие на воспитание и обучение.
Метод моделирования позволяет и более эффективно организовать конкретное психолого-педагогическое исследование. При теоретическом и эмпирическом подходах большое значение имеет интуиция исследователя. При исследовании мотивации методом моделирования значимость научной интуиции и практического опыта исследователя существенно возрастает, поскольку конкретная экспериментальная задача по разработке параметров модели складывается из двух постоянно чередующихся подзадач, решаемых поочередно в теоретическом, а затем в эмпирическом плане. В связи с этим продуктивное научное исследование такого типа должно базироваться на специальных процедурах и способах работы с экспериментами, использовать разработанные для этих целей методы анализа экспертных оценок. Для эффективного решения поставленной задачи необходимо участие нескольких экспертов, хотя в любом случае результат работы экспертной группы может рассматриваться лишь как рабочая гипотеза, требующая специальной экспериментальной проверки.
Для практической оценки меры проявления тех или иных смыслообразующих мотивов у конкретного индивида в конкретном виде деятельности нужна специальная экспериментальная диагностическая процедура. Задача усложняется еще и исключительными свойствами и положением предмета исследования – мотивация всегда относилась к самым интимным и трудно осознаваемым сторонам человеческой деятельности и психики. Поэтому в данном случае необходимо использовать специальные приемы и методы анализа, позволяющие выявить сущность явления.
Аналогия (от греч. analogia – соответствие, соразмерность) – это представление о каком-либо частном сходстве двух объектов, причем такое сходство может быть как существенным, так и несущественным. Существенность сходства или различия двух объектов условна и зависит от уровня абстрагирования (от лат. abstrahere – отвлекать), определяемого конечной целью исследования.
Гипотезы и аналогии должны обладать наглядностью или сводиться к удобным для исследования логическим схемам. Именно подобные логические схемы, упрощающие рассуждения и логические построения, а также позволяющие проводить эксперименты, приводящие к пониманию явлений природы, называют моделями.
Если результаты моделирования удовлетворяют исследователя и могут служить основой для прогнозирования поведения или свойств исследуемого объекта, то говорят, что модель адекватна (от лат. adaequatus – приравненный) объекту. При этом адекватность модели зависит от целей моделирования и принятых критериев.
В качестве одной из характеристик модели может выступать простота модели. Из двух моделей, позволяющих достичь желаемой цели и получить требуемый результат с заданной точностью, предпочтение должно быть отдано более простой. При этом адекватность и простота модели не всегда являются противоречивыми требованиями.
В качестве еще одного свойства модели можно рассматривать потенциальность модели (от лат. potentia – мощь, сила), или предсказательность с позиций возможности получения новых знаний об исследуемых объекте. Данное свойство модели подчеркивается в определении Н.Н. Моисеева [4]: «…модель содержит в себе потенциальное знание, которое человек, исследуя ее, может приобрести, сделать наглядным и использовать в своих практических жизненных нуждах». Именно свойство потенциальности позволяет модели выступать в качестве самостоятельного объекта исследования.
Хорошо построенная модель, как правило, доступнее, информативнее и удобнее для исследования, нежели реальный объект.
Самым важным предназначением моделей является их применение при изучении и прогнозировании поведения сложных процессов и явлений. Некоторые объекты и явления вообще не могут быть изучены непосредственным образом: широкомасштабные «натурные» эксперименты с экономикой страны или со здоровьем ее населения нежелательны, в силу своей дороговизны или рискованности для человека и /или среды его обитания. [5; 6]. Эксперименты на моделях с применением ЭВМ позволяют разработать план натурных экспериментов, выяснить требуемые характеристики измерительной аппаратуры, наметить сроки проведения наблюдений, а также оценить стоимость такого эксперимента.
Другое, не менее важное, предназначение моделей состоит в том, что с их помощью выявляются наиболее существенные факторы, формирующие те или иные свойства объекта, поскольку сама модель отражает лишь некоторые основные характеристики исходного объекта, учет которых необходим при исследовании того или иного процесса или явления.
Технология наглядного моделирования [7] позволяет стимулировать мотивации разного уровня и длительности. Моделирование своим объектом имеет модели. В исследовании Н.Г. Салминой разводятся понятия схемы и модели в учебной деятельности. Если модель не предполагает исследовательской функции, а применяется для иллюстрации каких-то положений или выступает как средство усвоения готового материала, то это схема, а вид знаково-символической деятельности – схематизация [1; 5].
Представление знаний связано со знаково-символической деятельностью и характеризуется структурированностью, связностью и активностью представления. Виды знаково-символической деятельности порождают тип моделей представления знаний, принятые в инженерии знаний и решений проблем искусственного интеллекта: логические, реляционные, семантические сети, продукционные, фреймовые.
Модель должна адекватно отражать основные, главные черты исследовательской деятельности обучаемых и должна быть описана математически; кроме того, необходимо учесть роль каждого определяющего структуру элемента, его функции и характеристики. Поэтому актуальной является проблема такой организации процесса обучения математике, когда представления, возникающие в мышлении обучаемых, отражают основные, существенные, ключевые стороны предметов, явлений и процессов, в том числе посредством адекватного моделирования и математического знания.
Именно формирование этих узловых, опорных качеств объекта восприятия (перцептивная модель) и представляет собой суть процесса наглядного моделирования. При этом особую значимость приобретают модели, фиксирующие процедуру математических действий в процессе исследовательской активности.
Наглядность – не только особое свойство психических процессов, но и свойство математического объекта в рамках учебного исследования. Наглядность математического объекта определяется, как уже отмечалось, факторами восприятия, представления, мнемическими процессами в их единстве на основе диагностируемого целеполагания. Следующие критерии определяют существо наглядности математического объекта:
– диагностируемое целеполагание целостности математического объекта (моделирование, кодирование, схематизация, замещение);
– понимание обучаемым сущности математического объекта (адекватность восприятия);
– устойчивость перцептивного образа и представления;
– познавательная и творческая активность обучаемого на основе комфортности и успешности обучения.
Первый и третий критерии обуславливаются проектированием ориентировочной основы учебной деятельности со знаково-символическими средствами учебного процесса, второй и четвертый – знаково-символической деятельностью обучаемого и обучающего.
Системная реализация в процессе исследовательского обучения математике всех видов наглядного моделирования выступает фактором формирования целостных образов математических объектов, неотъемлемым этапом имитации научного познания в обучении обучаемых, а значит, и значительно способствует усвоению математических знаний и развитию когнитивных способностей и математического мышления.
Наглядное моделирование – это формирование адекватного категории диагностично поставленной цели устойчивого результата внутренних действий обучаемого в процессе моделирования существенных свойств, отношений, связей и взаимодействий при непосредственном восприятии приемов знаково-символической деятельности с отдельными знаниями или упорядоченными наборами знаний [5; 6].
Таким образом, наглядное моделирование в обучении есть процесс, включающий в себя как проектирование и построение a priori модели (схемы, кода, заместителя), отражающей существо объекта восприятия, так и формирование адекватного результата внутренних действий обучаемых в процессе учебной деятельности. Использование «мягких математических моделей» [1] при создании ориентировочной и информационной основы учебной деятельности создает условия для оптимального управления познавательной деятельностью обучаемых.
Наглядное моделирование в процессе исследовательского поведения обучаемых создает основы для формирования положительной мотивации достижения результатов, самореализации личности и мотивации интеллектуального напряжения.
Таблица показывает прямые аналогии содержания понятия наглядного моделирования в обучении и требований к информационным моделям в инженерной психологии.
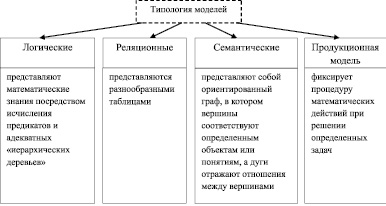
Типология моделей
Понятия наглядного моделирования
|
№ п/п |
Существенные связи наглядного моделирования в обучении |
Требования к проектированию информационных моделей в инженерной психологии |
|
1 |
Отражение существенных свойств, отношений, взаимодействий математических объектов и действий |
Модель представляет собой абстракцию, в которой сохраняются существенные свойства, отношения, взаимодействия |
|
2 |
Непосредственное восприятие математических объектов и действий |
Модель должна быть наглядной т.е. сведения, поставляемые моделью, должны быть восприняты быстро и без их кропотливого анализа |
|
3 |
Адекватность категории диагностично поставленной цели результатам внутренних действий обучаемых |
Модель должна быть геометрически подобной их (структурных компонентов объекта) действительному расположению |
|
4 |
Моделирование существенных свойств математических объектов и действий |
Модель имеет правильную организацию структуры (отбор того существенного и типичного, что позволяет с максимальной эффективностью донести существо реальной ситуации) |
|
5 |
Устойчивость результатов внутренних действий обучаемых, соответствие законам психологии восприятия |
Необходимо учитывать психофизиологические возможности человека |
Процесс объяснения, так же как и процесс наглядного моделирования в обучении математике, должен завершаться пониманием или адекватностью результатов внутренних действий обучаемых априорной модели (схемы). «Понимать объяснение – это … видеть сущность объясняемого в неразрывном единстве с конкретизацией этой сущности» (А.М. Сохор).
Подводя итог вышесказанному, отметим ключевые моменты, подтверждающие заключение о том, что моделирование выполняет интегративную функцию в обучении математике и инженерным дисциплинам.
Увеличивающийся объем информации в инженерной сфере, требующий выработки умения комплексно применять знания из различных дисциплин и способности к самостоятельному, творческому мышлению, противоречит дифференциации данных учебных дисциплин и создает предпосылки к их интеграции.
В качестве механизма управляемой интеграции можно выделить связи, плодотворное и целенаправленное осуществление которых на уровне знаний возможно за счёт использования естественнонаучных математических моделей, а на уровне видов деятельности – наглядного моделирования как структурообразующего фактора реализации профессиональной направленности.
Все сказанное выше оказывает существенное влияние на определение целей и содержания курса математики в вузах на инженерных специальностях и методику исследования профессионально-ориентированных задач на основе интеграции математических знаний и наглядного моделирования технических процессов в рамках указанного курса.
Библиографическая ссылка
Белоногова Е.А. МОДЕЛИРОВАНИЕ КАК ОСНОВНОЙ КОМПОНЕНТ НАГЛЯДНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ ИНЖЕНЕРОВ-БАКАЛАВРОВ // Современные наукоемкие технологии. 2016. № 2-1. С. 65-69;URL: https://top-technologies.ru/ru/article/view?id=35573 (дата обращения: 13.02.2026).



