Хорошо известно, что эффективность реализации любых технических решений зачастую не может достигать ожидаемого уровня из-за отсутствия в достаточной степени развитой теоретической базы. Именно это происходит в области создания современных нелинейных систем автоматического управления.
Вместе с тем системы управления такого рода нашли чрезвычайно широкое применение в системах управления роботов и манипуляторов, в станкостроении, в транспортной, авиационной, оборонной, ракетостроительной и других отраслях промышленности.
Современное состояние теории автоматического управления показывает, что успешного решения данной проблемы по всему комплексу показателей качества и для всего многообразия систем с единых математических и методологических позиций не найдено. Поэтому предпринимаются довольно успешные попытки создания общих теоретических подходов по отдельным направлениям проблемы [1].
Синтез систем является наиболее актуальной задачей современной теории управления. Для линейных систем эта задача решена в полной мере, для нелинейных систем далека от сколько-нибудь полного разрешения.
Рассматриваемые в работе нелинейные динамические системы являются наиболее употребимыми в современной инженерной деятельности, поэтому актуальны задачи синтеза именно таких систем.
Цель исследования
Показать преимущества использования Нλ-операторов при синтезе нелинейных динамических систем.
Материалы и методы исследования
В работе использованы методы теории систем и системного анализа, качественные методы нелинейного функционального анализа и теории нелинейных операторов. Методы, предложенные в диссертационной работе, могут быть использованы при решении таких практически значимых задач, как синтез нелинейных динамических систем и управление ими.
Результаты исследования и их обсуждение
Любой процесс управления включает в себя следующие основные этапы [8]:
– сбор и обработку информации о положении объекта управления в целях оценки сложившейся ситуации;
– принятие решения о наиболее целесообразных действиях;
– исполнение принятого решения.
Сбор информации о положении объекта управления заключается в измерении его координат, а также величин задающих и возмущающих воздействий. Для решения этой задачи используются различные измерительные устройства, образующие так называемую информационно-измерительную подсистему.
Обработка полученной информации имеет целью выработку на основании принятого закона управления управляющего сигнала, который должен обеспечить достижение цели управления. Обработка информации и принятие решения о необходимых действиях осуществляются в логико-вычислительной подсистеме.
Управляющие сигналы, полученные в логико-вычислительной подсистеме, поступают на исполнительную подсистему, которая приводит в действие регулирующие органы объекта управления, которые и решают задачу приведения его в требуемое положение. Совокупность объекта управления и управляющей подсистемы, в которую входят вышеперечисленные устройства (подсистемы), и образует систему автоматического управления (САУ).
Объект управления рассматривается как сколь угодно сложная система, преобразующая входные управляющие воздействия U(t) в выходные сигналы (траектории) V(t), характеризующие состояние объекта управления в момент времени t. Очевидно, что реальный объект управления может иметь множество входов и выходов, определяющих его функциональное взаимодействие с внешней средой.
Объект управления и воздействующее на него устройство управления образуют систему управления. Предполагается, что на объект управления действуют также возмущения ξ(t), изменяющие, как правило, в непредсказуемом направлении основные характеристики объекта управления.
Сигнал управления вырабатывается в соответствии с некоторой заданной целью управления, определяемой теми задачами, которые поставлены перед системой управления. Довольно часто в системах управления для выработки управляющих воздействий оказывается необходимой информация о действительном состоянии объекта управления. Эта информация поступает по цепи обратной связи.
Описание некоторого объекта как объекта управления и выявление каналов воздействия на него может производиться только исходя из заданной цели управления.
Математические вопросы теории управления включают в себя целый круг проблем анализа и синтеза.
При анализе полностью известна структура системы, заданы все ее параметры и требуется оценить какое-либо ее статическое или динамическое свойство. Под задачей анализа всякой системы подразумевается нахождение точного аналитического или приближенного решения соответствующей математической модели, описывающей рассматриваемую систему, и ее дальнейшее исследование в заданной области пространства состояний. Эта прямая задача хорошо разработана и широко применяется в инженерной практике для определения численными методами конструкции модели с известными параметрами.
Задачи синтеза обычно рассматриваются как обратные к задачам анализа, так как в них требуется определить как можно точнее структуру и параметры исходной системы по заданным критериям качества, и преследуют рациональный выбор исходных параметров и основных характеристик рассматриваемой системы. Указанное направление в технике принято называть проектированием или синтезом систем регулирования и управления. Его характерной чертой является стремление к нахождению оптимальных решений при определенных технических условиях среды, в которой находится рассматриваемая динамическая система [4].
Как известно, главной задачей теории автоматического регулирования следует считать создание методов синтеза. В настоящее время разработка и проектирование систем автоматического регулирования является сложной задачей. Здесь можно наметить следующие основные этапы.
1. Изучение объекта регулирования, определение его характеристик, параметров, условий работы и воздействий, которые он испытывает.
2. Формулирование требований к системе регулирования.
3. Выбор первоначальной схемы регулирования.
4. Выбор элементов схемы регулирования на основе требований к их мощности, надёжности имеющихся источников питания, эксплуатационных требований и т.д.
5. Определение характеристик системы регулирования, обеспечивающих выполнение требований по статике и динамике.
6. Уточнение структурной схемы регулирования, определение необходимых корректирующих средств, окончательный выбор и расчёт элементов и параметров системы регулирования.
7. Теоретический анализ спроектированной системы, построение переходных процессов, частотных характеристик, исследование влияния различных управляющих и возмущающих воздействий.
8. Экспериментальное исследование спроектированной системы и внесение корректировок в схему.
9. Проектирование и монтаж системы регулирования.
10. Наладка системы регулирования в реальных условиях работы и опытная эксплуатация.
Как известно, изучение общей проблемы синтеза нелинейных динамических систем в ряде ситуаций существенно упрощается, если их рассматривать с позиций операторного подхода.
Остановимся вкратце на некоторых часто встречающихся в инженерной практике нелинейных операторов в динамических системах. В случае модели нелинейной системы ее структуру, как правило, представляют в виде комбинаций более простых звеньев: линейного и функционального, предполагая, что в функциональном звене длительность переходного процесса пренебрежимо мала. Нелинейные операторы, входящие в интегральную модель, – это, как правило [7]:
- нелинейный оператор суперпозиции Немыцкого:
;
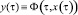- нелинейный интегральный оператор Гаммерштейна:
;
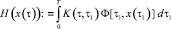- нелинейный интегральный оператор Урысона:
;
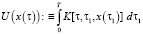- оператор Лихтенштейна – Ляпунова:
.
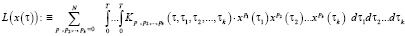Естественно, что не все нелинейные системы поддаются описанию моделями типа вышеуказанных с помощью операторов, связывающих в явном виде вход системы с ее выходом. Если, например, в рассматриваемой нелинейной динамической системе существует обратная связь, то эта система описывается операторным уравнением вида
,
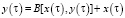где В – нелинейный оператор. Так, в динамических системах контроля и учета электроэнергии, являющихся следящими, оператор В часто удается представить в виде нелинейного интегрального оператора Гаммерштейна Н.
Как оказалось, вышеперечисленные нелинейные интегральные операторы являются Н-операторами, подчиняющимися условию
,
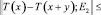
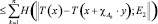где функция H∈Ф(L), для каждого элемента y∈E1 и для всех попарно дизъюнктных измеримых подмножеств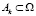 
, 
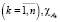– индикатор подмножества Ak.
Пусть Е1 и Е2 – два ЛОФП измеримых по Лебегу функций, оператор А: Е1 → М,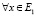 
. Назовем оператор А Нλ-оператором, если для 
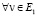выполняется условие
,
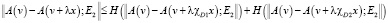где функция Н: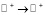 
принадлежит классу F(L), для каждого элемента x∈E1 и для любых измеримых подмножеств D1 и D2 из Ω таких, что 
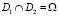и 
, 
– и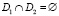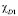ндикатор множества Di, i = 1,2 и 
.
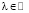Частными примерами Нλ-оператора А являются: оператор суперпозиции (Немыцкого), нелинейные атомические интегральные операторы Гаммерштейна, Урысона, интегро-степенные ряды Вольтерра, нормальные интегранты, локально определенные операторы [2].
Оператор T: Е0 → Е1 назовем суперлинейным, если [5]
,
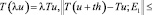
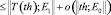где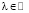 
, 
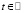, и, th∈Е0.
Примерами суперлинейных операторов являются:
1. Всякий непрерывный выпуклый функционал Г. Достаточно выбрать t0 настолько малым, чтобы число Г(u + th) имело одинаковый знак с Г(u) при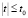 
. Тогда из выпуклости функционала Г вытекает
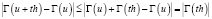
при всех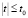 
.
2. Нелинейный интегральный оператор Урысона
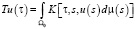
в паре F-квазинормированных пространств будет суперлинейным, если его ядро подчиняется условиям:
а) K(τ, s, λu) = λK(τ, s, u) при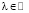 
.
б)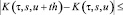 
.
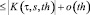3. Достаточным условием суперлинейности оператора Немыцкого fu(s) = f[s, u, (s)], где f – нормальный интегрант (в частности, каратеодориева функция), является однородностью функции f(s,u) по u при каждом s и выполнение ограничения
.
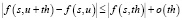Оператор H: S(X) → S(Y) называется локально определенным оператором [2], если для любого множества А∈Σ и любых двух функций x1 и x2 из S(X), совпадающих на А почти всюду, их образы Нx1 и Нx2 также совпадают почти всюду на А.
Локально определенные операторы являются более широким классом операторов суперпозиции, охватывающим Н-операторы, с характеристиками в виде К-функций и более общего вида.
В публикациях последнего времени, посвященных синтезу динамических систем, большое внимание уделяется свойствам и роли так называемых доминированных линейных и нелинейных операторов, входящих в модель рассматриваемой системы. Теория мажорирования представляется перспективной для вышеуказанных систем идеей мажорирования операторов. Теория таких нелинейных операторов, действующих в локально невыпуклых топологических пространствах, – интересная и исключительно важная в прикладном аспекте область функционального анализа. Если оператор мажорируется другим оператором, называемым доминантой, то свойства последнего существенно влияют на свойства первого. Так, для случая произвольной пары локально ограниченных пространств измеримых функций, и заданных каратеодориевых ядер К1 и К2 нами показано, что при условии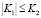 
нелинейный интегральный оператор с ядром К1 наследует нужные «хорошие» свойства оператора, содержащего ядро К2 [2].
Нелинейные динамические системы, описываемые нелинейными обыкновенными дифференциальными уравнениями, целесообразно сводить к отвечающим им нелинейным интегральным уравнениям.
Несмотря на наличие значительного числа работ, синтез как метод построения оптимальных систем только начинает развиваться, что объясняется прежде всего сложностью задач синтеза. Целый ряд задач синтеза, имеющих существенное значение для практики, еще ждет своего решения, в особенности это относится к нелинейным системам.
Заключение
Таким образом, в данной работе развита модель нелинейных динамических систем, а именно показано преимущество использования нелинейных Нl-операторов, являющихся обобщением нелинейных интегральных операторов, для описания нелинейной динамической системы при синтезе.
Библиографическая ссылка
Фетисов В.Г., Панина И.И. ОПЕРАТОРНЫЙ ПОДХОД В СИНТЕЗЕ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ // Современные наукоемкие технологии. – 2016. – № 2-1. – С. 34-37;URL: https://top-technologies.ru/ru/article/view?id=35567 (дата обращения: 21.11.2024).