Проблемы управления сложными системами связаны с избыточным количеством параметров, характеризующих состояние системы. Сбор и обработка данных обо всех параметрах является очень сложной и дорогой процедурой. Однако отказаться от нее невозможно в силу необходимости получения актуальных и достоверных данных для принятия и реализации управленческих решений. Таким образом, необходимо искать способы и пути сокращения числа контролируемых параметров, создавать алгоритмы, позволяющие прогнозировать наличие нежелательных процессов в контролируемой системе, выработать рекомендации для более детального анализа отдельных систем (или групп систем) среды обитания.
Одним из способов сокращения числа контролируемых параметров является факторизация множества параметров, т.е. разбиение их на относительно независимые группы. Принцип факторизации позволяет изучить каждый тип объектов по отдельности, а затем рассмотреть всю систему в целом. Тем самым достигается возможность применить достаточно хорошо известные методы и процедуры теорий управления, информации, вероятности и других наук на практике без значительных затрат на предварительную разработку подробных математических моделей и создать практически реализуемую универсальную концепцию интеллектуальной среды обитания (ИСО), состоящую из управляемых и взаимодействующих объектов. В результате можно не только прогнозировать развитие ИСО и объектов, ее составляющих, но и корректировать состояние конкретных объектов и проектировать подсистемы управления с учетом полученных результатов.
В настоящей работе рассмотрен энтропийный подход к мониторингу, в котором, на основе математических процедур, вытекающих из теории информационного взаимодействия объектов [1], создаются информационные феноменологические модели сложных динамических систем. Разработанная методология позволяет эффективно использовать энтропийный подход к оценке устойчивости систем.
Мониторинг на основе анализа динамики энтропии
Понятие энтропии является одним из ключевых понятий термодинамики и теории информации, а также находит свое применение в ряде других наук, предметом исследования и изучения которых являются сложные стохастические системы. Возможности использования энтропии и энтропийного моделирования в настоящее время активно исследуются в социально-экономических системах, например в работах [5, 2].
Использование энтропии в различных отраслях науки обуславливает различные подходы к ее интерпретации. В термодинамике под энтропией, введенной Р. Клаузисом, понимается величина, являющаяся функцией состояния системы и определяющая меру рассеяния энергии системы [7]. В теории информации под энтропией, введенной Шенноном, понимается мера неопределенности информации в системе [3]. Однако на семантическом уровне связь энтропий объясняется тем, что при получении системой некоторого количества информации ее информационная энтропия увеличивается, при этом для обработки информации требуется совершение работы, что, в свою очередь, приводит к росту энтропии термодинамической. Таким образом, закономерности изменения энтропии в разных разрезах при одинаковых условиях одинаковы, что позволяет при дальнейшем рассмотрении не разделять энтропию на термодинамическую и информационную. При этом, несмотря на разницу в интерпретации, математическая форма определения энтропии остается идентичной для термодинамики и теории информации, что хорошо показано в работе [4].
Для сложных стохастических систем, в т.ч. социально-экономических, энтропия является характеристикой динамической устойчивости системы – ключевого свойства системы с точки зрения системного подхода и общей теории систем. Это дает возможность использовать энтропию в качестве интегрального параметра мониторинга состояния социально-экономической системы.
Сложности прикладного применения энтропии в качестве интегрального параметра в ее классической интерпретации по отношению к реальным социально-экономическим системам заключаются главным образом в невозможности получения ее точного значения, которое бы системно учитывало все факторы, влияющие на динамику системы. Однако косвенная оценка энтропии возможна путем оценки скорости изменения параметров системы.
Очевидно, что при изменении какого-либо из параметров количество информации, необходимое для описания текущего состояния системы, меняется, следовательно, меняется ее энтропия. Скорость изменения параметров системы, а следовательно, и скорость изменения энтропии характеризуют динамику системы относительно внешней окружающей среды. Робастная оценка скорости изменения дает возможность прогнозировать будущее состояние системы, используя классические инструменты технического анализа. Справедливо и обратное: при изменении энтропии количество информации в описании системы меняется, следовательно, параметры описания системы изменились. При этом, если скорость изменения параметров системы не соответствует скорости изменения внешней окружающей среды, система выходит из состояния динамического равновесия. Об этом свидетельствует критическое изменение выходных параметров системы и их отклонение от прогнозных значений. Свойство аддитивности энтропии позволяет идентифицировать отклонения в отдельных элементах системы на основе анализа феноменологической модели.
Однако количество параметров, характеризующих состояние системы, избыточно. Это, во-первых, затрудняет процедуру мониторинга; во-вторых, увеличивает время реакции на принятие и реализацию управленческих решений. Одним из возможных способов сокращения количества исследуемых параметров является их факторизация.
Факторизация параметров мониторинга и феноменологическая модель сложной динамической системы
Факторизация параметров мониторинга предполагает разбиение множества параметров, характеризующих состояние системы, на относительно независимые группы. При этом предполагается, что группы параметров, а также параметры внутри групп имеют причинно-следственную связь.
Разбиение параметров мониторинга проводится по уровням иерархии системы; при этом в рамках одного уровня может быть выделено несколько групп параметров, связанных между собой технологическим циклом и информационным взаимодействием. При факторизации группы параметров выделяются таким образом, что характеризуют состояние отдельных элементов (подсистем).
Декомпозиция сложной динамической системы на подсистемы по уровням иерархии проводится по объектам управления с учетом горизонта управления (стратегического, операционного и оперативного) и характера деятельности (управляющей, основной, обеспечивающей). Общее количество подсистем определяется структурой системы. Использование феноменологической модели позволяет не учитывать внутреннюю структуру в процессе факторизации.
Феноменологический подход к анализу управляемой системы ориентируется на обобщенные характеристики, которые оцениваются по входным и выходным информационным потокам. Преобразование входных информационных потоков и сигналов в выходные описывается неизменным между циклами мониторинга оператором G, являющимся математическим описанием модели системы или ее элементов. При этом под циклом мониторинга понимается период (или интервал между отсчетами) между калибровками системы, т.е. такого внешнего воздействия или изменения входных информационных потоков, которое при отклонении фактических значений результатов мониторинга от прогнозируемых сохраняет устойчивость системы.
В общем случае, оператор G является нелинейным оператором. Однако в рассматриваемом подходе принимается, что на интервале между отсчетами, осуществляемыми в процессе мониторинга, оператор G является линейным (кусочно-линейная аппроксимация). Для обеспечения этого условия интервал между отсчетами выбирается достаточно коротким и равным технологическому циклу на выбранном уровне иерархии (фактически ограниченной возможностью технологической реализации такого интервала определяется применимость рассматриваемой модели). Другими словами, чем динамичнее система и чем меньше ее инерционность по отношению к внешним воздействиям, тем короче должен быть интервал, чтобы обеспечить достаточную точность линейного прогнозирования выходных сигналов и эффективность отрицательных обратных связей, обеспечивающих стабильность. Если прогнозируемые значения оцениваемых параметров отличаются от измеренных настолько, что не могут быть объяснены наличием случайных погрешностей измерения, то необходимо произвести робастное оценивание изменений на основе короткой выборки из нескольких отсчетов и принять решение о необходимости внешнего воздействия на систему для восстановления ее состояния. Для углубленного анализа причин отклонений и типа воздействия проводится анализ «базы знаний» и/или привлекается эксперт, чтобы провести обследование отдельных подсистем в соответствии со структурной моделью системы. При внешнем воздействии оператор G будет соответственно изменен и, как это следует из теории управления, должна осуществляться калибровка системы (соответственно и параметров ее модели), чтобы сохранить устойчивость системы.
Таким образом, оператор G может изменяться в промежутках на основе управленческих решений в процессе адаптации системы к внешним воздействиям и (или) на основе алгоритма самообучения. Таким образом, множество выходных информационных потоков и сигналов {u} описывается как
{u} = G({х},{y}), (1)
где{x} – предсказуемые (предопределенные) входные параметры системы или ее элемента, полученные от стандартных партнеров по информационному взаимодействию и являющиеся функциями времени;
{y} – «случайные» входные параметры системы или ее элемента, обусловленные воздействием внешней среды и также являющиеся функциями времени.
Изменение выходных информационных потоков и сигналов {u} определяется первой производной по времени от входных информационных потоков и сигналов, т.е.
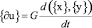 . (2)
. (2)
Скорость изменения выходных информационных потоков и сигналов {∂2u} определяется второй производной по времени от входных информационных потоков и сигналов, т.е.
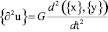 . (3)
. (3)
При этом, время для формул (1), (2) и (3) определяется длительностью периода мониторинга.
Формулы (1), (2) и (3) справедливы как для системы, так и для отдельных ее элементов (подсистем).
Предсказуемые входные сигналы {x}, поступающие в систему, не влияют на устойчивость системы, поскольку являются заранее предопределенными таким образом, что служат основой для прогнозирования динамики изменения выходных параметров.
Сложная динамическая система находится в постоянном взаимодействии с внешней окружающей средой, что обуславливает постоянное изменение параметра {y}. Постоянное изменение «случайных» входных сигналов увеличивает энтропию системы, выводя ее из состояния динамического равновесия, за счет увеличения количества неизвестной информации в системе, а также за счет необходимости совершения дополнительной работы на обработку такой информации. В случае, если система не успевает обработать «случайные» входные сигналы в рамках одного цикла мониторинга, т.е. не успевает вернуться в состояние динамического равновесия, значения скорости изменения выходных информационных потоков будут сильно отличаться от пороговых, что свидетельствует о необходимости применения нелинейных методов управления и анализа причин отклонений. Скорость обработки «случайных» входных сигналов зависит также от состава сигнала – количества полезной информации и шумов, содержащихся в нем.
В случае, когда значения «случайных» входных сигналов равны нулю или на протяжении нескольких циклов мониторинга не меняются, энтропия системы остается неизменной; скорость изменения выходных информационных потоков не меняется. В соответствии с законами теории информации и термодинамики это свидетельствует о том, что система находится в таком состоянии динамического равновесия, что стремится к состоянию стагнации, близкому к изолированности системы и теряет способность быстрой адаптации под изменения внешней окружающей среды.
Подходы к выбору параметров мониторинга
Специфика оценки устойчивости социально-экономической системы по данным мониторинга связана со следующими факторами:
1) наличием одновременно технических и социальных подсистем, между которыми имеется информационное взаимодействие;
2) невозможностью и нецелесообразностью существования технических подсистем без социальных;
3) существованием различных целей и интересов у групп, входящих в социальную подсистему, которые не всегда задаются управляющим органом и могут быть описаны рассматриваемым выше оператором G.
Приведенные факторы обуславливают выбор в качестве интегральных параметров мониторинга социально-экономической системы целей заинтересованных сторон и индикаторов их достижения; в качестве отдельных параметров мониторинга – целей и индикаторов, определенных на основе факторной модели и включающих параметры технической подсистемы. При этом при определении интегральных параметров необходимо учитывать как формальные цели, так и неформальное влияние заинтересованных сторон на динамику системы.
Для определения формальных целей используются современные методологии управления по целям в социально-экономических системах – теория заинтересованных сторон, система сбалансированных показателей Нортона и Каплана, рассматриваемые в настоящей работе, и другие практики управления.
На первом этапе определения интегральных параметров балансовая модель ресурсных отношений, разработанная в рамках теории заинтересованных сторон, позволяет определить основные цели и артефакты обмена в социально-экономической системе, определяя таким образом выходные информационные потоки и сигналы верхнего уровня иерархии.
Полученные в результате формирования балансовой модели ресурсных отношений цели и артефакты обмена являются основными целями для формирования сбалансированной системы показателей Нортона и Каплана [6].
Алгоритм формирования интегральных параметров мониторинга повторяется на каждом уровне иерархии системы с учетом причинно-следственных взаимосвязей между уровнями иерархии. Далее, для каждого уровня иерархии строится факторная модель и определяются входные информационные потоки.
Для определения неформальных параметров, характеризующих влияние человеческого фактора на рассматриваемую систему, вводится понятие симбиотических групп или объединений. Под симбиотической группой или объединением рассматривается группа взаимодействующих неформально участников системы, вектора интересов которых близки по направлению, и осуществляющих согласованные действия с целью удовлетворения личных интересов. Определение вектора интереса полностью соответствует определению вектора мотивации. Значение вектора меняется в пределах от 0 до 1 и определяется мерой удовлетворенности владельцев связи; при этом значение вектора имеет вероятностный характер. Установление неформальных связей носит как случайный, так и спланированный характер.
Таким образом, симбиотическое объединение или группа формируют некоторую нерегламентированную подсистему в рамках уже существующей системы деятельности. При этом, в случае, если стохастический вектор интересов владельцев симбиотической связи близок по направлению с целевым вектором системы, то скорость возвращения системы в состояние динамического равновесия при внешних воздействиях и динамика изменения интегральных параметров будут высоки; система быстро развивается и переходит на новый качественный уровень жизненного цикла. В случае, если вектора не совпадают по направлению, то наблюдается противоположный результат: система не успевает вернуться в состояние динамического равновесия в рамках одного цикла мониторинга; энтропия возрастает, система приходит в состояние, близкое к «тепловой смерти», не успевая при этом адаптироваться под внешнюю среду.
Симбиотическая группа или объединение включаются в совокупность формальных параметров мониторинга как стохастический вектор интересов владельцев связи на соответствующем горизонте и уровне иерархии управления и обуславливает появление нечетких данных мониторинга. Количество векторов при этом определяется исходя из факта, что один владелец может иметь связь не более чем с семью и не менее чем с тремя другими владельцами одного уровня иерархии и не более чем с двумя владельцами других уровней управления.
Полученные таким образом интегральные и частные параметры и входные информационные потоки, а также причинно-следственные связи между ними используются для оценки устойчивости системы в соответствии с формулами (1), (2) и (3).
Анализ и использование результатов мониторинга
На каждом периоде мониторинга на основе робастной оценки скорости изменения выходных параметров на предыдущих циклах формируется прогнозное значение динамики выходных параметров. Полученные в результате мониторинга данные сравниваются с прогнозными; статистические отклонения и условия, при которых они были получены, фиксируются в базе знаний («Data Knowledge»). В базе знаний хранится онтологическое описание предыдущих типовых и сходных ситуаций для рассматриваемой или аналогичной системы. База знаний непрерывно обновляется, образуя «интеллектуальную» основу системы принятия решений, сочетающую решения экспертов-управленцев и автоматических экспертов, действующих на основе опыта, заложенного в их алгоритмах и базе знаний.
В процессе эксплуатации системы в течение всего жизненного цикла осуществляется экспертная оценка проектов управленческих решений по результатам их воздействия на текущее состояние системы. Решение об использовании того или иного проекта принимается руководителем соответствующего уровня управления или автоматически, с помощью интеллектуального алгоритма, который учитывает возможные последствия выполненных решений.
Алгоритм мониторинга в соответствии с рассматриваемым подходом приведен на рисунке.
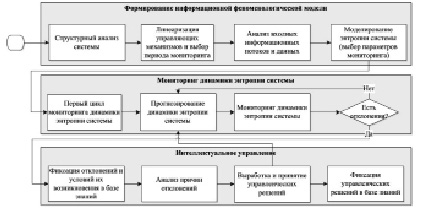
Алгоритм мониторинга на основе энтропийного подхода
Заключение
В настоящей статье рассмотрен подход к мониторингу сложной динамической системы, основанный на энтропийном подходе к оценке устойчивости в соответствии с информационной феноменологической моделью системы. К ключевым результатам относятся следующие выводы:
1. Мониторинг сложных социально-экономических систем, включающих технические составляющие, может быть успешно реализован на основе энтропийного подхода с использованием феноменологической модели системы.
2. Оптимизация набора наблюдаемых параметров и выбор периодичности мониторинга основан на формировании интегральных параметров, являющихся функциями входных и выходных информационных потоков.
3. Особенности мониторинга социально-экономической системы заключаются в необходимости учитывать нечеткие данные, обусловленные человеческим фактором вместе с более или менее точно определенными оценками технических параметров системы.
4. Нечеткие данные включаются в набор параметров мониторинга путем анализа и учета существующих и перспективных симбиотических групп социально-экономической системы.
5. Рассмотренный подход позволяет минимизировать количество параметров, наблюдаемых в процессе мониторинга, снизить требования к инфокоммуникационным каналам, корректно оценить динамику системы и прогнозировать возникающие признаки неустойчивости.
6. Принятие управленческих решений осуществляется соответствующим лицом или автоматически, на основе обновляемой в процессе жизненного цикла системы базы знаний, в которой сосредотачивается предшествующий опыт эксплуатации системы и ее аналогов.
7. Рассмотренный подход не привязан к конкретной прикладной области и может быть использован в различных системах, для которых характерно совмещение принципов нечеткой логики и детерминированных технических систем.
Библиографическая ссылка
Горелик С.Л., Марков Я.Г., Чернышкова М.А. МОНИТОРИНГ СЛОЖНЫХ СИСТЕМ НА ОСНОВЕ ФЕНОМЕНОЛОГИЧЕСКОЙ МОДЕЛИ // Современные наукоемкие технологии. 2016. № 2-1. С. 13-18;URL: https://top-technologies.ru/ru/article/view?id=35563 (дата обращения: 13.03.2026).



