В течение всей истории существования криптографии самым важным свойством шифра являлась и является до сих пор его стойкость – возможность алгоритма противостоять атакам. Чем больше времени и ресурсов требуется для взлома шифра, тем большей стойкостью он обладает. Существует несколько способов анализа стойкости алгоритма, одним из которых является слайдовая (сдвиговая) атака [4].
Слайдовая атака – криптографическая атака на основе подобранного открытого текста, которая позволяет проводить криптоанализ многораундовых блочных шифров [9]. Впервые такой вид атак был предложен Алексом Бирюковым и Дэвидом Вагнером в 1999 году.
Основой слайдовой атаки являются два понятия:
1. Идентичность раундов шифрования – для каждого раунда функция F() одинаковая;
2. Возможность нахождения ключа –зная текст на входе и на выходе любого раунда, можно найти K, зная P и F(P).
Простейшая слайдовая атака представлена на рис. 1.
Идея заключается в сопоставлении двух процессов шифрования между собой таким образом, что один из них будет отставать от другого на один раунд. После нахождения слайдовой пары можно вычислить некоторые биты подключа. Для нахождения оставшихся битов необходимо найти другу слайдовую пару и провести анализ уже с ее помощью. В результате нахождения нескольких слайдовых пар возможно нахождение всех битов ключа [1].
Рассмотрим, насколько применима слайдовая атака для алгоритма Магма.
Магма представляет собой симметричный блочный шифр, основанный на ГОСТ 29147-89, для которого зафиксированы блоки замены, с размером блока данных 64 бита, секретным ключом 256 бит и 32 раундами шифрования [6]. Магма основана на сети Фейстеля, модифицируется только одна половина сообщения, что позволяет сравнить левую часть P и правую часть P’. Рассмотрим алгоритм слайдовой атаки для различных комбинаций ключа.
В алгоритме Магма, так же, как и в стандарте ГОСТ 28147-89, не предусмотрена функция выработки подключей, что позволяет ослабить алгоритм, апеллируя определенными значениями ключа. Также не стоит забывать, что последние 8 элементов ключа инвертируются, но в данных примерах этот факт опускается.
Для начала рассмотрим случай, когда все подключи имеют одинаковое значение. Т.к. объем одного элемента ключа составляет 32 бита, то существует 232 вариант ключа (из всего ключевого пространства 2256, для которых все раундовые подключи будут иметь одинаковые значения. Опираясь на Парадокс Дней Рождений (ПДР), который гласит, что достаточно перебрать 2N/2 значений тестов для получения слайдовой пары с вероятностью 0,5, нам достаточно будет опробовать 216 различных вариантов. Так как алгоритм Магма построен по схеме Фейстеля, то в соответствии с рис. 1, правая половина текста Р (32 бита) будет совпадать с левой половиной текста Р’.
Процесс шифрования будет выглядеть аналогично представленному на рис. 1. Пусть входные тексты Р и Р’ будут представлены в виде двух половин текстов (PL, PR) и (PL1, PR1) соответственно, а выходные тексты E и E1 – из (EL, ER) и (EL1, ER1). В этом случае для нахождения слайдовой пары достаточно, чтобы выполнялось тождество PL = PR1.
Рассмотрим, как будет выглядеть поиск слайдовой пары при наличии двух подключей, которые циклически повторяются, то есть
К1 = К3 = К5 = К7 и К2 = К4 = К6 = К8. (1)
Всего существует 264 варианта исходного секретного ключа из всего ключевого пространства 2256, для которых будут выполняться равенства (1). В качестве допущения примем, что раундовые подключи не меняют порядок следования в последних раундах шифрования. В отличие от первого рассмотренного случая, в этом случае поиск необходимо вести по всему диапазону возможных входных значений в алгоритм шифрования. В соответствии с ПДР, можно ожидать, что слайдовая пара будет найдена при переборе всего 232 вариантов открытых текстов.
На рис. 2 предоставлена схема сопоставления раундов шифрования с запаздыванием на 2 раунда.
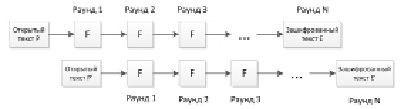
Рис. 1. Простейшая реализация слайдовой атаки
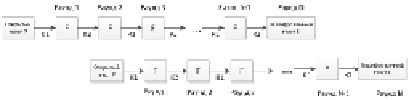
Рис. 2. Схема шифрования с запаздыванием на два раунда

Рис. 3. Процесс зашифрования со сдвигом на 4 раунда
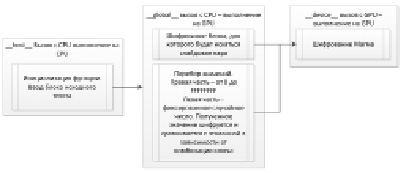
Рис. 4. Схема работы программы поиска слайдовой пары
Обозначим левую и правую часть первого открытого текста PL и PR соответственно, второго PL1 и PR2 соответственно. Сопоставив схему с рис. 2 и схему Фейстеля, получим следующие равенства:
PR⊕PL1 = F(PR, K1);
PL1 ⊕PR = F(PR1, K2).
Аналогично определяется связь шифр- текстов EL, ER и EL1, ER2:
EL1 ⊕ER = F(ER1, K2);
EL⊕ER1 = F(ER, K1);
В заключении рассмотрим случай, когда исходный секретный ключ будет состоять из двух равных половин по 128 бит. Сделаем допущение о том, что раундовые подключи не меняют порядок следования в последних раундах шифрования. В этом случае будет четыре уникальных раундовых подключа, которые циклически повторяются. То есть будут выполняться следующие равенства:
К1 = К5, К2 = К6, К3 = К7, К4 = К8.
В данном случае полный перебор ключевого пространства будет составлять 2128 опробования. А для ПДР это количество будет равно 265, но с вероятностью нахождения слайдовой пары 0,5.
Сопоставим процессы зашифрования с запаздыванием на 4 раунда, как показано на рис. 3.
Связи между исходными и шифр-текстами для первого (PL, PR, EL, ER) и второго (PL1, PR1, EL1, ER1) процессов шифрования будут выглядеть следующим образом:
PL⊕ F(PR, K1) ⊕ PL1 =
= F((PR1 ⊕ F(PL1, K4)), K3);
ER⊕ F(EL, K1) ⊕ ER1 =
= F((EL1 ⊕ F(ER1, K4)), K3).
В ходе данного исследования была разработана программа для поиска слайдовых пар с использованием технологии параллельных вычислений NVIDIACUDA [2, 3, 6]. За её основу была взята более ранняя программа «Шифрование криптографическим алгоритмом Магма с использованием технологии параллельных вычислений NVIDIACUDA». В новой программе считается, что для анализа мы используем модель Черного ящика. То есть данные шифруются одним и тем де ключом. Наша задача заключается в нахождении этого ключа. Мы можем подавать на вход открытые тексты и считывать шифрованные. Анализируя их, найти слайдовую пару и сделать предположение о ключе. На рис. 4 представлена общая схема работы программы.
Разберем подробнее схему, предоставленную на рис. 4. В функции main задается эталонный (для которого будем искать слайдовые пары) блок шифрования, выделяется память на GPU и вызывается функция с приставкой __global__ , обозначающая, что функция вызывается на CPU, а ее вычисления происходят на GPU. Внутри данной функции на нулевом потоке производится непосредственно шифрование эталонного блока с использованием функции, разработанной в более ранней программе, с той лишь разницей, что теперь функция имеет приставку __device__, которая обозначает, что функция вызывается и выполняется только на GPU. Поиск слайдовой пары основан на переборе требуемого набора значений. Левая часть блока заполняется фиксированным псевдослучайным числом, которое выработано на основе функции времени, а правая часть непосредственно перебирается. Затем эталонный шифр-тест сравнивается с перебираемым на основе требуемых условий.
Рассмотрим вышеописанный алгоритм на примерах из кода [8]. Память на GPU выделяется следующим образом:
intcnt = 0; //Host переменная
int *dev_cnt; //Device переменная
cudaMalloc( (void**)&dev_cnt, sizeof(int) ); //выделение памяти для переменной на device
cudaMemcpy(dev_cnt, &cnt, sizeof(int), cudaMemcpyHostToDevice); //копирование значения переменной с host на device
Выработка псевдослучайного числа происходит следующим образом:
srand ( time(NULL) ); //создание метки времени
intrandint = rand() % N; //получение случайного значение от 0 до N, где N = 2147483647 (231 – 1)
Непосредственный вызов __global__ функции выглядит довольно просто:
pair_search<<<1, 512>>>(dev_block, dev_cnt, dev_randint, dev_ar); // аргументами функции выступают эталонный блок, переменная для получения количества слайдовых пар, фиксированное псевдослучайное число, массив для получения найденных слайдовых пар. В <<<>>> скобках представлены числа, обозначающие количества блоков и количества потоков. 512 выбрано в качестве оптимального числа потоков.
Теперь рассмотрим внутренность функции pair_search:
intLE = *EL>> 32; //получение LE и RE для шифрования эталонной пары
int RE = *EL& 0xffffffff;
int et = 0;
if ( 0 == threadIdx.x) //шифрование эталонного блока происходит на 0 потоке
{
et= encrypt(LE, RE, 0);
}
int it = 0
for (inti = 0; i < 65536 / blockDim.x; ++i) // перебор 216 значений
{
intPR1 = threadIdx.x + i * blockDim.x; //в ER1 записывается число от 0 до 65535, распараллеливаясь при этом на 512 потоков
ER1 = encrypt(*randint, PR1, 1); //шифрование перебираемого блока. Первым аргументом идет фиксированное псевдослучайное число, рассмотренное выше.\
if ( ER1 ==et) //проверка условия (данный пример для одинаковых подключей)
{
++*cnt; //инкрементирование переменной количества слайдовых пар
if (it< 5) //проверка и запись первых пяти найденных слайдовых пар
{
*ar[it] = PR1;
}
++it;
}
}
Таблица 1
Время вычисления для поиска пары при шифровании только одной части (PR1)
|
Количество потоков |
Время, мс |
|
1 |
8680 |
|
8 |
2357 |
|
16 |
2079 |
|
64 |
559 |
|
128 |
357 |
|
256 |
241 |
|
512 |
125 |
|
1024 |
120 |
Не стоит также забывать о том, что вычисления на GPU происходят асинхронно как между потоками, так и с GPU. Поэтому необходимо создать точку синхронизации:
cudaEvent_tstart; //инициализация точки синхронизации
cudaEventCreate(&start ); //создаем event
pair_search<<<1, 512>>>(dev_block, dev_cnt, dev_randint); //вызов функции
cudaEventRecord( start, 0 ) ; //записываем event
cudaEventSynchronize( start ) ; //синхронизируем event
cudaMemcpy(&ar, dev_ar, sizeof(int)*5, cudaMemcpyDeviceToHost); // получение массива найденных слайдовых пар с GPU на CPU
cudaMemcpy(&cnt, dev_cnt, sizeof(int), cudaMemcpyDeviceToHost); // получение количества найденных слайдовых пар с GPU на CPU
Таблица 2
Примеры найденных слайдовых пар
|
Исходное значение |
Ключ |
Слайдовая пара |
|
P – 0xfedcba9876543210 E – 0xe9ec4191bad969b9 |
0xffeeddccffeeddccffeeddccffeeddccffeeddccffeeddccffeeddccffeeddcc |
P1 – 0x7654321028da3b14 E1 – 0xbad969b9ef04eacb |
|
P – 0x1111111111111111 E – 0xe52d6d84bcf784ec |
0x1111111111111111111111111111111111111111111111111111111111111111 |
P1 – 0x11111111b8382606 E1 –0xbcf784ec6552d11e |
|
P – 0xffffffffffffffff E – 0x8727ffdcd2f88b5 |
0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff |
P1 – 0xffffffff9a7806c7 E1 – 0xcd2f88b5eb81ab2a |
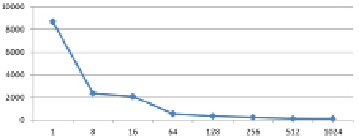
Рис. 5. Зависимость времени выполнения от количества параллельных потоков
Одной из целей данного исследования был временной аспект поиска слайдовой пары [1]. Вычисления производились на ПК Inteli5 2400 NVIDIAGTS 459 8 GbRAM. Поиск слайдовых пар (по сути это перебор значений от 0 до 65525 с использованием их в качестве входных данной функции) занимает порядка 100–150 мс.
На табл. 1 представлена зависимость времени поиска от количества потоков.
На рис. 5 приведен график по данным из табл. 1.
Как видно из вышеприведенного графика, при увеличении количества потоков, время уменьшается, что является довольно закономерным результатом.
Результаты найденных слайдовых пар представлены в табл. 2.
Работа выполнена при поддержке гранта РФФИ № 15-37-20007-мол-а-вед.
Библиографическая ссылка
Ищукова Е.А., Богданов К.И., Бабенко Л.К. СЛАЙДОВАЯ АТАКА НА КРИПТОГРАФИЧЕСКИЙ АЛГОРИТМ МАГМА И ЕЁ РЕАЛИЗАЦИЯ С ИСПОЛЬЗОВАНИЕМ ТЕХНОЛОГИИ ПАРАЛЛЕЛЬНОГО ВЫЧИСЛЕНИЯ NVIDIACUDA // Современные наукоемкие технологии. 2016. № 1. С. 25-29;URL: https://top-technologies.ru/ru/article/view?id=35486 (дата обращения: 11.03.2026).



