Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Климов А.В. 1 Главный В.Г. 1 Кротов С.В. 1 Куликов Д.В. 1 Меледин В.Г. 1

---

1 ФГБУН «Институт теплофизики им. С.С. Кутателадзе Сибирского отделения Российской академии наук»

Предложен высокоразрешающий алгоритм для дальномеров с линейной частотной модуляцией (ЛЧМ) зондирующего сигнала, комбинирующий идеи обработки сигнала окном Гаусса, преобразования Фурье и обработки спектральной плотности мощности методом центра масс. Показано, что разрешение ЛЧМ-дальномера определяется разрешением вычислительных алгоритмов идентификации частоты сигнала, что определяет актуальность и практическую значимость создания новых алгоритмов высокого разрешения для ЛЧМ-дальномера. Выполнен сравнительный анализ предложенного и известных методов спектрального анализа – устойчивого метода Фурье фиксированного разрешения и основанных на определении параметров предполагаемой модели сигнала менее устойчивых сверхразрешающих алгоритмов. На основе результатов сравнения, численного и физического экспериментов показано, что использование разработанного высокоразрешающего алгоритма существенно улучшает разрешение, точность и устойчивость ЛЧМ-дальномеров.

Статья в формате PDF

2931 KB

лчм-дальномер

высокое разрешение

алгоритмы обработки сигналов

центр масс

окно гаусса

численное моделирование

экспериментальная установка

тестирование качества алгоритмов

1. Марпл-мл С.Л. Цифровой спектральный анализ и его приложения. – М.: Мир, 1990. – 584 с.

2. Оппенгейм А.B. Цифровая обработка сигналов / А.B. Оппенгейм, Р.B. Шафер. – 5-е изд. – М.: Техносфера, 2006. – 856 с.

3. Самарский А.А., Гулин А.В. Численные методы. – M.: Наука, 1989. – 432 с.

4. Hyun E. Method to Improve Range and Velocity Error Using De-interleaving and Frequency Interpolation for Automotive FMCW Radars / E. Hyun, J. H. Lee // International Journal of Signal Processing, Image Processing and Pattern Recognition. – 2009. – Vol. 2, № 2. – P. 11–22.

5. Im Y.T. A DDS and PLL-based X-band FMCW radar system / Y. T. Im J, H. Lee, S. O. Park // Intelligent Radio for Future Personal Terminals (IMWS-IRFPT), 2011 IEEE MTT-S International Microwave Workshop Series on. – P. 1–2.

6. Investigation of spectral centroid features for cognitive load classi?cation / P.N. Le, E.Ambikairajaha, J. Epps, V. Sethua, E.H.C. Choi // Speech communication. – 2011. – Vol. 53, № 4. – P. 540–551.

7. Laser ranging: a critical review of usual techniques for distance measurement / M. C. Amann, T. B.M. Lescure, R. Myllyla, M. Rioux // Optical Engineering. – 2001. Vol. 40, № 1. – P. 10–19.

8. Skolnik M. I. Introduction to Radar Systems. – McGraw-Hill, 1980. – 581 p.

9. Stelzer A. Resolution Enhancement with Model-Based Frequency Estimation Algorithms in Radar Signal Processing / A. Stelzer M. Pichler // Subsurface Sensing Technologies and Applications. – 2003. – Vol. 4, № 3. – P. 241–261.

Лазерная дальнометрия как метод определения расстояний до объектов основана на зондировании и обработке отраженного сигнала. Наиболее распространены дальномеры, зондирующий сигнал которых подвергается линейной частотной модуляции (ЛЧМ, в зарубежной литературе – FMCW). Подобные ЛЧМ-дальномеры обладают наилучшими характеристиками на малых и средних расстояниях [7]. Задача развития высокоразрешающих методов обработки сигналов для повышения точности и расширения функциональных возможностей ЛЧМ-дальномеров, в полной мере, актуальна.

Структура ЛЧМ-дальномера представлена на рис. 1.

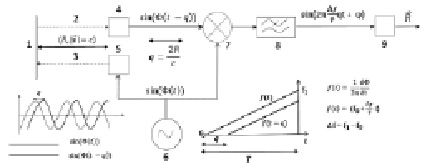
Рис. 1. Структура ЛЧМ-дальномера. 1 – объект, 2 – отраженный сигнал, 3 – зондирующий – сигнал, 4 – приемник, 5 – источник, 6 – генератор сигнала, 7 – смеситель, 8 – фильтр низких частот, 9 – вычислитель

Генерируемый опорный ЛЧМ периодический сигнал преобразуется на источнике излучения в сигнал, зондирующий объект. Отраженный сигнал через время q прохождения сигнала до объекта и обратно попадает на приемник. Смеситель частот переданного и принятого ЛЧМ сигналов в последовательном соединении с низкочастотным фильтром позволяют получить фрагмент периодического сигнала, частота которого пропорциональна расстоянию до объекта. После дискретизации дальность до объекта алгоритмически определяется на основе расчета частоты сигнала по набору его дискретных значений.

При обработке сигнала 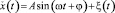по дискретной выборке 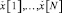необходимо найти оценку 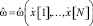частоты ω, где ξ(t) – случайный шумовой процесс, 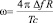, ?f – разность частот в ЛЧМ, R – расстояние до объекта, c – скорость распространения сигнала до объекта и обратно, T – период ЛЧМ.

Задача определения частоты периодического сигнала относится к классу задач спектрального анализа, для которых за многие годы был разработан и теоретически обоснован ряд методов [1]. Базовым алгоритмом определения частоты сигнала в ЛЧМ-дальномерах считается алгоритм Фурье, имеющий фиксированное разрешение, равное 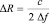, и определяемое шириной полосы ЛЧМ [8]. Дополнение нулями исходного сигнала длины N позволяет интерполировать значения спектральной плотности мощности (СПМ) сигнала между N исходными значениями СПМ. Это приводит к увеличению вычислительной стоимости, но улучшению разрешения базового алгоритма Фурье, что было использовано в работе [4] при проектировании ЛЧМ-дальномера.

Для достижения сверхразрешения при определении частоты сигнала используют класс алгоритмов, основанный на определении параметров предполагаемой модели сигнала. К ним относят методы Писаренко и методы Прони, оценивающие сумму комплексных экспонент в шуме, и ряд других методов. В работе [9] модифицированные аналоги методов Писаренко и Прони были применены для обработки сигнала ЛЧМ-дальномеров.

Недостатком сверхразрешающих методов является плохая обусловленность решаемой обратной задачи и необходимость адекватности использованных моделей. В совокупности все это приводит к меньшей устойчивости алгоритмов по сравнению с алгоритмами фиксированного разрешения. Выбранный авторами подход к определению частоты сигнала с одной стороны улучшает точность рассмотренных выше методов спектрального анализа с фиксированным разрешением, а с другой стороны, обеспечивает повышение устойчивости по сравнению со сверхразрешающими алгоритмами.

Алгоритм центра масс (spectral centroid) применяется в спектральном анализе [6] для поиска центра тяжести спектрального пика, определяющего оценку частоты сигнала. Метод упомянут в [9] в качестве возможного подхода к обработке сигнала ЛЧМ-дальномера и использован в [5] при реализации прибора. Метод по разрешению превосходит метод Фурье, так как является интегральным, и устойчив, так как решает прямую непараметрическую задачу. Важной частью предлагаемого авторами подхода является оконная предобработка сигнала, активно применяемая с 1940-х годов для улучшения свойств анализируемой СПМ сигнала [1, 2], таких как ширина и уровень главного и боковых лепестков. В данной работе мы используем обработку сигнала окном Гаусса.

Предложенный высокоразрешающий алгоритм для ЛЧМ-дальномера основан на суперпозиции идей оконной обработки сигнала, построении его СПМ и вычислении центра тяжести данной СПМ. Несмотря на упоминание метода «центра масс» для ЛЧМ-дальномеров в работах [5, 9], ни в одной из них не показана возможность его эффективного использования в сочетании с обработкой окном.

Предлагаемый алгоритм для ЛЧМ-дальномера

Задача определения дальности до объекта в ЛЧМ-дальномерах сводится к задаче определения частоты фрагмента периодического сигнала. Теоретическим фундаментом для алгоритмов определения частоты сигнала типа «центр масс» является следующая теорема.

Теорема 1. Пусть S(ω) – СПМ, определим формулу «центра масс»:

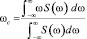. (1)

Если S(ω) – симметрична относительно ω1, то центр масс совпадает с центром симметрии, то есть ωc = ω1.

Доказательство. Достаточно в верхнем интеграле сделать замену ω2 = ω – ω1, после чего разбить интеграл на сумму двух интегралов, первый из которых равен нулю в силу нечетности функции, а второй равен

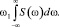
Можно ввести приближение формулы (1) для сеточной функции 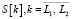, заданной с шагом hw, применяя численное интегрирование методом прямоугольников [3]:

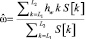. (2)

Предлагаемый алгоритм для определения частоты сигнала ЛЧМ-дальномера реализуется следующим образом. Фрагмент периодического сигнала 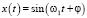перемножается с функцией Гаусса с таким параметром σ2, чтобы 99 % ее энергии приходилось на носитель. Используемое для обработки сигнала окно Гаусса близко по норме к функции Гаусса, и можно считать, что его преобразование Фурье также является функцией Гаусса [2]. Тогда, предполагая, что частота сигнала ω1 намного больше ширины полосы СПМ функции Гаусса, можно считать, что СПМ сигнала x(t), обработанного окном Гаусса, равна

.

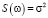
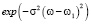Ввиду симметричности СПМ S(ω) относительно ω1, для нее верна Теорема 1, и алгоритм (2) применяется для оценки частоты сигнала ω1.

Особенностью предложенного алгоритма для ЛЧМ-дальномера является предварительная обработка окном Гаусса. Выбор окна обусловлен получением гладкой СПМ, позволяющей получать приближение (2) формулы (1) с меньшей, по сравнению с традиционными прямоугольными окнами, ошибкой численного интегрирования [3].

Для тестирования предложенного алгоритма численно промоделирована измерительная схема дальномера, описанная во введении. В численных экспериментах параметры модели были заданы следующим образом: частота генератора FDDS = 256 МГц, разность частот в ЛЧМ ?f = 20 МГц, время модуляции T = 32,768 мс, максимальная задержка qmax = 16,384 мс, частота дискретизации после НЧ фильтра FS = 1 МГц, число отсчетов оцифрованного анализируемого сигнала N = 16384. На анализируемый сигнал был наложен гауссовский шум, отношение «сигнал-шум» = 5. На рис. 2 показан пример сигнала, численно смоделированного в данной схеме и обрабатываемого алгоритмами для определения расстояния.

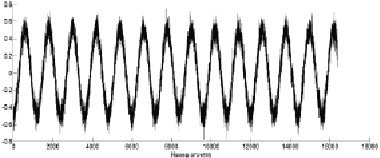
Рис. 2. Пример модельного сигнала ЛЧМ-дальномера

Проведено сравнение предложенного алгоритма с известными применяемыми при обработке сигналов ЛЧМ-дальномеров алгоритмами. Сравнение проводилось на 1000 экспериментах, в которых расстояние до объекта задавалось случайно в диапазоне R∈[200, 2000]. Гистограммы ошибок методов приведены на рис. 3. Хорошо видно, что ширина гистограммы является наименьшей у метода центра масс с окном Гаусса, а метод обеспечивает статистически наименьшую погрешность.

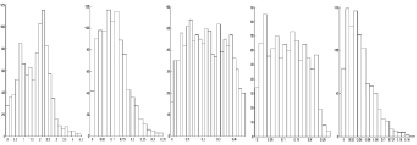
Рис. 3. Гистограмма ошибок алгоритмов для модельных сигналов ЛЧМ-дальномера. По оси X – абсолютная ошибка алгоритма, м. По оси Y – количество экспериментов, для которых ошибка попала в заданный интервал. Алгоритмы слева направо: центр масс с прямоугольным окном, метод Прони, метод Писаренко, метод Фурье с дополнением сигнала нулями, центр масс с окном Гаусса

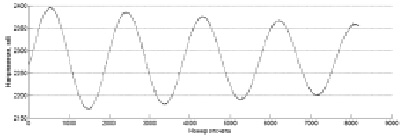
Рис. 4. Пример экспериментального сигнала ЛЧМ-дальномера

Таблица 1

Относительные погрешности методов ( %) для различных расстояний (м)

Дополнительно проведены 100 независимых численных экспериментов для каждого из 10 различных расстояний, равномерно расположенных на интервале [500, 561] метров, в которых вычислялись дальность и относительная ошибка. Выбор диапазона расстояний обусловлен тем, что при заданных параметрах численной модели шаг сетки для СПМ соответствует интервалу 61 метр. Соответственно, при последовательном моделировании расстояния в данном диапазоне пик СПМ равномерно смещается относительно узла сетки СПМ, что лучше позволяет протестировать спектральные методы анализа сигналов.

Данные экспериментов приведены в табл. 1. Они показывают, что ошибка метода центра масс с окном Гаусса на порядок меньше ошибки остальных методов, и подтверждают высокое разрешение предложенного алгоритма.

Для дополнительной верификации работы алгоритма на экспериментальных данных создан макет электронной измерительной схемы, аппаратно моделирующий тракт стандартного ЛЧМ-дальномера. Процессы зондирования объекта и отражения от него сигнала вместе с самим объектом были реализованы при помощи радиоимпульсных передатчика и приемника, а звено задержки – при помощи коаксиального кабеля.

Таблица 2

Относительные погрешности методов ( %) для различных длин кабеля (м)

Задача определения дальности сводилась к определению длины кабеля. Основные параметры были заданы следующим образом: FDDS = 256 МГц, ?f = 20 МГц, T = 9,216 мс, qmax = 1,024 мс, FS = 1 МГц, N = 8192. Оцифрованный сигнал собирался в микроконтроллере, откуда по COM-порту передавался на стационарный компьютер и анализировался в среде Matlab. Особенностью экспериментального сигнала, пример которого показан на рис. 4, является хорошее отношение «сигнал-шум», получаемое из-за относительно малой длины кабеля и отсутствия эффектов многолучевого рассеяния, а также некоторая паразитная модуляция амплитуды, обусловленная неидеальностью фильтров электронной схемы.

Для сравнения алгоритмов кабель удлинялся несколькими способами. Проводились тесты на относительную разницу в показаниях алгоритмов для исходного и удлиненного кабелей. Предложенная экспериментальная методика хорошо детектирует разрешение алгоритмов и позволяет определять чувствительность методов к небольшим изменениям положения объекта. Для удлинения исходного кабеля к нему присоединялись отрезки с длинами 0,077, 0,483, 0,585, 1,093 метров и коэффициентом замедления, равным 0,7 скорости света. Для каждого составного кабеля осуществлялось 100 независимых измерений длины, и вычисленный результат каждого из алгоритмов усреднялся по этим измерениям.

Результаты эксперимента приведены в табл. 2. Чувствительность нового алгоритма к изменению длины кабеля оказалась наилучшей среди тестируемых методов, что дополнительно подтвердило его высокое разрешение и перспективы практического использования.

Заключение

Рассмотрена проблема повышения разрешения ЛЧМ-дальномера, актуальная для систем с высокими требованиями к точности определения дальности до объекта. Показана сводимость задачи определения расстояния ЛЧМ-дальномером к алгоритмическому определению частоты фрагмента периодического сигнала. Предложен новый высокоразрешающий алгоритм для ЛЧМ-дальномера, комбинирующий идеи обработки сигнала окном Гаусса, преобразования Фурье и обработки спектральной плотности мощности методом центра масс. При численном моделировании схемы ЛЧМ-дальномера показано, что новый алгоритм превосходит в несколько раз по разрешению известные и применяемые при проектировании ЛЧМ-дальномеров методы спектрального анализа. Эффективность и точность предложенного алгоритма для ЛЧМ-дальномера подтверждена при тестировании на экспериментальной установке, подтвердившем перспективность и важность для практических приложений разработанного высокоразрешающего алгоритма для ЛЧМ-дальномера.

Работа выполнена при поддержке гранта РНФ № 14-29-00093.

Библиографическая ссылка