Сушка – этап послеуборочной обработки зерна, от которого зависит его дальнейшая сохранность, предназначен для удаления избыточного количества влаги из зернового материала. Известно, что наиболее распространенной является конвективная сушка, которая характеризуется наличием агента сушки (нагретый воздух) и агента охлаждения (атмосферный воздух), которые выполняют две функции: изменение температуры; удаление испаренной влаги за пределы зерносушилки [4].
Конвективный способ подразделяется на четыре зоны: нагрев зерна; период постоянной скорости сушки; период убывающей скорости сушки; охлаждение. Интенсивность этого процесса зависит от температуры и скорости агентов сушки и охлаждения, а также от продолжительности нагрева и охлаждения. Временно-температурные показатели процесса влагоудаления отражены в кинетике сушки [7].
Определение времени сушки и времени охлаждения одной зерновки (как и любого другого тела) описывается выражением Ньютона-Рихмана [3]:
сМΔТ = ατS(Ta – Tз), (1)
где с – теплоемкость зерновки, Дж/кг °С;
М – масса одной зерновки, кг;
ΔТ – изменение температуры зерновки, °С;
α – коэффициент теплоотдачи, Вт/м2 °С;
τ – время нагрева или охлаждения, с;
S – площадь поверхности зерновки, м2;
Та – температура агента сушки (охлаждения), °С;
Тз – начальная температура зерновки, °С.
Представленное выражение (1) позволило сформулировать цель исследований – выявить влияние температурно-влажностных параметров агента сушки (охлаждения) на коэффициент теплоотдачи.
Для решения поставленной цели были сформулированы следующие задачи исследования:
– определить значение коэффициента теплоотдачи для влажного воздуха;
– определить коэффициент теплоотдачи для сухого воздуха;
– определить коэффициент теплоотдачи для насыщенного пара;
– оценить влияние влажности воздуха на коэффициент теплоотдачи влажного воздуха для диапазона параметров, ограниченных кинетикой сушки.
Материалы и методы исследования
Объект исследования: коэффициент теплоотдачи влажного воздуха при конвективной сушке зерен пшеницы.
Методы исследования: статистический и аналитический анализы.
Результаты исследования и их обсуждение
Учеными СибНИПТИП сформулирована концепция интенсификации процессов переработки биосырья, основанная на активизации гидроаэродинамического взаимодействия энергоносителя и объекта обработки [3]. Основываясь на данной концепции, была предложена схема сушки зернового материала на базе теплонасосной установки.
Известно, что влажный воздух представляет собой смесь сухого воздуха и насыщенного пара [1].
Если разделить поток влажного воздуха на два параллельных потока сухого воздуха и насыщенного пара, то произведение эквивалентной теплоемкости на площадь определится по выражению (2) [10]
αS = αсв·Sсв + αнп·Sнп, (2)
где α – коэффициент теплоотдачи влажного воздуха, Вт/м2 °С;
αсв – коэффициент теплоотдачи сухого воздуха, Вт/м2 °С;
αнп – коэффициент теплоотдачи насыщенного пара, Вт/м2 °С;
S – площадь теплоотдачи, м2;
Sсв – площадь теплоотдачи от сухого воздуха, м2;
Sнп – площадь теплоотдачи от насыщенного пара, м2.
Для расчета соотношений площадей насыщенного пара и сухого воздуха была составлена расчетная схема (рис. 1) при постоянном значении атмосферного давления.

Рис. 1. расчетная схема для определения соотношений площадей. Примечание: dx – толщина слоя, м; Vнп – объем, занимаемый насыщенным паром, м3; Vсв – объем, занимаемый сухим воздухом, м3; mнп – масса насыщенного пара, кг; mсв – масса сухого воздуха, кг; ρнп – плотность насыщенного пара, кг/м3; ρсв – плотность сухого воздуха, кг/м3
Соотношение площадей насыщенного пара и сухого воздуха будет определяться по выражению
К = Sнп/Sсв = Sнп·dx/(Sсв·dx) = Vнп/Vсв, (3)
где К – коэффициент соотношения площадей теплоотдачи.
Известно, что произведение объемов на плотности есть масса, поэтому:
К = Vнп/Vсв = mнп·ρсв/(mсв·ρнп). (4)
Соотношение масс, содержащихся в выражении (4), определяется из выражения влагосодержания влажного воздуха (5):
mнп/mсв = d/1000, (5)
где d – влагосодержание влажного воздуха, г/кг.
Соотношение плотностей – это функция от температуры, т.к. плотность сухого воздуха и насыщенного пара при постоянном давлении зависят только от температуры (6), что видно из данных, которые были получены при анализе физических свойств сухого воздуха и насыщенного пара. По результатам анализа было определено соотношение плотностей сухого воздуха к насыщенному пару [2].
Результаты расчетов соотношения плотностей сухого воздуха к насыщенному пару представлены на рис. 2.
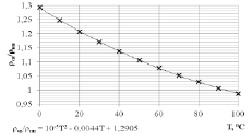
Рис. 2. Соотношение плотностей сухого воздуха к насыщенному пару в зависимости от температуры
Из графика (рис. 2) видно, что с увеличением температуры влажного воздуха, соотношение сухого воздуха к насыщенному пару уменьшается нелинейно (1,207 при Т = 20 °С; 1,106 при Т = 50 °С; 1,052 при Т = 70 °С). Зависимость соотношения плотностей от температуры представлена следующим выражением:
ρсв/ρнп = f(T) = 10-3·(10-5·T2 –
– 0,0044·T + 1,2905), (6)
где Т – температура воздуха, °С.
Подставив (6) и (5) в (4), получили:
К = d·10-6·(10-5·T2 –
– 0,0044·T + 1,2905) = Sнп/Sсв. (7)
Откуда следует, что:
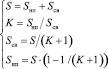 . (8)
. (8)
Подставив систему уравнений (8) в выражение (2), получили:
αS = αсв·Sсв + αнп·Sнп = = αсв·S·(1/(K + 1)) + αнп·S·(1 – 1/(K + 1))
или
α = αсв·(1/(K + 1)) + αнп·(1 – 1/(K + 1)). (9)
Данное выражение (9) показывает взаимосвязь коэффициента теплоотдачи влажного воздуха по данным коэффициентов теплоотдачи сухого воздуха и насыщенного пара в зависимости от температуры.
Коэффициент теплоотдачи α при естественной конвекции определяется из выражения [5]:
Nu = C(Gr·Pr)n·(Pr/Prст)0,25, (10)
где Nu = α·l/λ – критерий Нуссельта,
где l = 2·L·A/(L + A) – гидравлический диаметр, м;
L = 4,2 – 8,6·10-3 – длина зерновки, м;
A = 1,6-4·10-3 – толщина зерновки, м;
Gr = g·l3·β·ΔT/ν2 – критерий Грасгофа;
где β – коэффициент температурного расширения, К-1;
ΔТ – разность температур поверхностей теплообмена, °С;
ν – коэффициент кинематической вязкости, м2/с.
Pr = ν/a = c·µ/λ – критерий Прандтля;
где a – коэффициент температуропроводности, м2/с;
с- удельная теплоемкость, Дж/кг·К;
µ – динамическая вязкость, Па·с
λ – коэффициент теплопроводности, Вт/м·К
С – для ламинарного режима С = 1,18;
n – для ламинарного режима n = 0,125.
При этом коэффициент теплоотдачи определили из выражения:
α = 1,18·g0,125·β0,125×
×ΔT0,125·Pr0,375·λ/Prст0,25·l0,625·ν0,25. (11)
На основании физических данных сухого воздуха получено следующее значение коэффициента теплоотдачи:
αсв = 1,57·10-3·l– 0.625·(|Tагента – Тзерна|)0,125×
×0,49635·(0,0148·Тагента + 11,234)/
/(0,9169 – 6·10-5·Tзерна),
где Тагента – температура агента сушки (охлаждения), °С;
Тзерна – температура поверхности зерна, °С.
Заменив части выражения, содержащие переменные температур, коэффициентом В = f(Тагента;Тзерна), получим:
αсв = 1,57·10-3·l-0,625·Bсв(Тагента; Тзерна), (12)
где
Всв = (|Tагента – Тзерна|)0,125·0,46935×
×(0,0148·Тагента + 11,234)/(0,9169 – 6·10-5·Tзерна);
αнп = 1,57·10-3·l– 0.625·(|Tагента – Тзерна|)0,125·(0,0013·Т3агента – 0,272·Т2агента + + 18,801·Tагента + 1045,3)/(1,8976 + 7·10-5·Т2зерна – 0,0139·Tзерна)
или
αнп = 1,57·10-3·l– 0,625·Bнп(Тагента; Тзерна), (13)
где
Внп = (|Tагента – Тзерна|)0,125·(0,0013·Т3агента – 0,272·Т2агента + 18,801·Tагента + 1045,3)/ (1,8976 + 7·10-5·Т2зерна – 0,0139·Tзерна)
Для анализа полученной зависимости использована компьютерная программа MathCad [9], график зависимостей представлен на рис. 3.
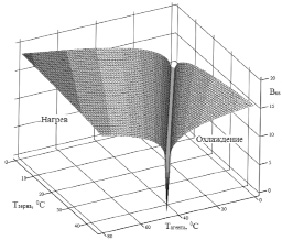
Рис. 3. Значение коэффициента Ввв в зависимости от температуры агента и зерновки
Учитывая полученные данные коэффициента теплоотдачи сухого воздуха и насыщенного пара, коэффициент теплоотдачи влажного воздуха представит собой следующее выражение:
α = 1,57·10-3·l– 0,625·(Bсв/(К + 1) + Внп·(1 – 1/
(К + 1)))= 1,57·10– 3·l– 0,625·B(Та;Тз;φ), (14)
где φ = f(d;Та) – относительная влажность, %.
При сушке зерен пшеницы в семенном режиме, нормативными документами установлены следующие ограничения [8]:
Тагента = 0..80 °С;
Тзерна = 0..45 °С;
φ = 0..100 %.
Выявлено, что при таких ограничениях влажность воздуха не оказывает существенного изменения коэффициента В = Bсв/(К + 1) + Внп·(1 – 1/(К + 1)). Коэффициент примерно равен коэффициенту сухого воздуха (максимальное значение В = 1,08·Всв при Та = 80; Тз = 45; φ = 100 %), вследствие чего влажностью воздуха можно пренебречь.
Следовательно, в процессе сушки зерен пшеницы в семенном режиме коэффициент теплоотдачи от агента зерновке может быть определен по выражению:
α = 1,57·10– 3·l– 0.625·(|Tагента – Тзерна|)0,125·0,49635×
×(0,0148·Тагента + 11,234)/(0,9169 – 6·10– 5·Tзерна),
или
α = 10– 3·l– 0.625·Ввв, (15)
где
Ввв = 1,57·(|Tагента – Тзерна|)0,125·0,49635×
×(0,0148·Тагента + 11,234)/(0,9169 – 6·10– 5·Tзерна).
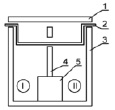
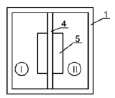
Для экспериментального подтверждения полученных теоретических данных значения коэффициента теплоотдачи влажного воздуха разработана лабораторная установка на базе теплового насоса (рис. 4).
а) б) в)


г) д)
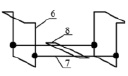
Рис. 4. Лабораторная установка. а – вид спереди; б – вид сверху; в – штатив с подвижным лотком; г – общий вид; д – вид внутри, I – камера охлаждения; II – камера нагрева, 1 – съемная крышка; 2 – штатив с подвижным лотком; 3 – корпус; 4 – перегородка; 5 теплонасосная установка; 6 – вертикальные ручки штатива; 7 – горизонтальные балки; 8 – лоток подвижный
Установка лабораторная состоит из корпуса 3, выполненного из теплоизоляционного материала. Внутри корпуса расположена теплонасосная установка 5, предназначенная для получения агента нагрева и агента охлаждения. Внутренняя полость корпуса 3 разделена теплоизоляционной перегородкой 4, которая делит внутреннее пространство на две камеры – охлаждения (I) и нагрева (II). В верхней части корпуса 3 предусмотрена установка штатива 2, эскиз которого представлен на рисунке. Верхняя часть оборудована съемной крышкой 1, выполненной из того же теплоизоляционного материала, что и корпус 3. Съемная крышка предназначена для обеспечения доступа в камеры охлаждения (I) и нагрева (II).
Штатив состоит из ручек 6, опирающихся на верхнюю часть корпуса, горизонтальных балок 7, перемещающихся вертикально по ручкам 6, и лотка 8 из перфорированного материала, обеспечивающего свободное движение агента.
Лабораторная установка обладает следующими техническими характеристиками:
ДхШхВ – 1х1х1 м; объем камеры нагрева Vн = 0,5 м3; объем камеры охлаждения Vо = 0,5 м3; теплопроизводительность ТНУ Qту = 2,5 кВт; холодопроизводительность ТНУ Qху = 2,0 кВт; мощность номинальная электрическая потребляемая из сети Рн = 0,5 кВт
Зависимость изменения температур воздуха камеры нагрева (Тк) и камеры охлаждения (Тв) при различных начальных температурах окружающего воздуха представлена на рис. 5.
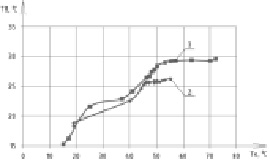
Рис. 5. Зависимость температуры сушильного агента, полученного тепловым насосом, от температуры конденсатора. 1 – начальная температура воздуха + 15,3 °С; 2 – начальная температура воздуха + 19 °С
Выводы
По результатам проведенной работы получены следующие выводы:
1. Выявлена закономерность влияния температуры на коэффициент теплоотдачи для влажного воздуха, которая описывается выражением (9).
2. Смоделирована зависимость коэффициента теплоотдачи для сухого воздуха в зависимости от температуры (выражение (12)).
3. Смоделирована зависимость коэффициента теплоотдачи для насыщенного пара (выражение (13)).
4. Выполнена оценка влияния влажности воздуха на коэффициент теплоотдачи.
5. На основании полученных результатов была разработана лабораторная установка зерносушилки на базе теплового насоса.
Библиографическая ссылка
Кизуров А.С., Кокошин С.Н., Лапшин И.П. КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ ОТ АГЕНТА СУШКИ ЗЕРНОВКЕ ПРИ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ // Современные наукоемкие технологии. 2015. № 12-5. С. 790-795;URL: https://top-technologies.ru/ru/article/view?id=35372 (дата обращения: 31.01.2026).



